Channel Coding
2
• Channel coding provides to the receiver the ability of
error detection and correction
• Channel Encoder adds some redundant bits to the input
bit sequence. Addition of these extra bits
• Allows the receiver to perform error detection and
correction
• However, increases the bit rate and hence increase
required bandwidth

Types of Error Control
• Error detection and retransmission
 The receiver does not attempt to correct the error
 The receiver simply requests a retransmission
 Require full duplex connection
 Example:
o Automatic Retransmission reQuest (ARQ)
• Forward error correction (FEC)
 The receiver can correct and detect the errors
 Require Simplex Connection
 Example:
o Block Codes
o Convolutional Codes

4
Linear block codes
• The information bit stream is divided into blocks of k bits.
• Each block is encoded to a larger block of n bits.
• The coded bits are modulated and sent over channel.
• The reverse procedure is done at the receiver.
• Structure of Codeword
Data block
Channel
encoder
Codeword
k bits n bits
p1, p2,……pn-k m1m2,….mk
n-k parity bits k message bits
n bit codeword

Error Control Coding
• A binary block code generates a block of n coded bits
from k information bits. We call this an (n,k) binary
block code.
• The n codeword symbols can take on 2n possible values
corresponding to all possible combinations of the n
binary bits.
• 2k codewords from these 2npossibilities is to be selected
to form the code, such that each k bit information block
is uniquely mapped to one of these 2k codewords.
• A code is said to be linear if addition (modulo-2 adition)
of any two codewords in the code produce a third code
word in the code
• A code is systematic code, if the first (or last) k
elements in the codeword are information bits
5

Linear Block Code
• The encoding operation of Linear Block code involve two
operations
 Segmentation of information sequences
 Transformation of each message block into a block of n bits
according to some predetermined set of rules
• Consider
Message block
 Each message bit can be 0 or 1 => 2k distinct message blocks
• Each message block is transformed to codeword C of length
n bits
• There will be 2k distinct codewords, one unique codeword for
each distinct message
6
),...,,,,...,,(),...,,(
bitsmessage
21
bitsparity
2121
   kknn mmmpppcccC 
),...,,( 21 kmmmm 
),...,,( 21 ncccC 

Linear Block Code
• In Systematic block code
• In matrix form
7
,...,1,
.........
.........
,22,11,
,12121111
nknknfor imc
and
mpmpmpc
mpmpmpc
ii
kknkkkkn
kkn






















100
010
001
][
,21
,22221
,11211
21





knkkk
kn
kn
k
ppp
ppp
ppp
mmmC

Linear Block Code
•
8
mGC 
matrixParity)(
matrixidentity
matrixGenerator][
knk
kkk
nkk


 
P
I
IPG
 
















100
010
001
,21
,22221
,11211





knkkk
kn
kn
k
ppp
ppp
ppp
IPG

Linear Block Code
• The generator matrix is a compact description of how
codewords are generated from information bits in a
linear block code.
• The design goal in linear block codes is to find generator
matrices such that
 the corresponding codes are easy to encode and decode
 yet have powerful error correction/detection capabilities.
• Tradeoffs between
 Efficiency
 Reliability
 Encoding/Decoding complexity
9

Linear Block Code
• Parity Check Matrix: Associated to each (n,k) linear
block code there is a parity check matrix H at the
decoder.
• Parity check matrix H has its rows orthogonal to rows of
G such that
• The parity check matrix H is used to detect errors in the
received code
• C is the codeword in (n,k) block code generated by G iff
10
0T
GH
  nkn
T
kn PIH , 
0T
CH

Linear Block Code
• Let R = C + E be the received message where C is the
correct code and E is the error
• Decoding operation is done by determining syndrome vector
S as
• If R is a valid vector then syndrome of received vector S is 0
• Nonzero S indicates that there are errors in transmission
• Thus S is used to detect the errors. It is also used to correct
the errors.
• The errors can be corrected at the receiver by comparing S
with the rows of and correcting the ith received bit if S
matches with the ith row of 11
T
TT
T
EH
EHCH
RHS



T
H
T
H

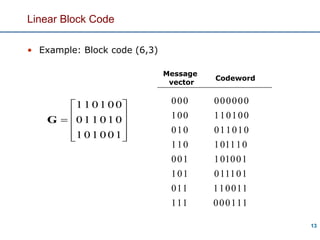
Linear Block Code
Operations of the generator matrix and the parity check matrix
• Example1: For a (6,3)LBC with generator matrix G, find
codeword for all the distinct messages.
12










1
0
0
0
1
0
0
0
1
1
1
0
0
1
1
1
0
1
G

13
Linear Block Code
• Example: Block code (6,3)











1
0
0
0
1
0
0
0
1
1
1
0
0
1
1
1
0
1
G
1
1
1
1
1
0
0
0
0
1
0
1
1
1
1
1
1
0
1
1
0
0
0
1
1
0
1
1
1
1
1
0
0
0
1
1
1
1
0
0
0
1
1
0
1
0
0
0
1
0
0
0
1
0
1
0
0
1
1
0
0
1
0
0
0
0
1
0
0
0
1
0
Message
vector
Codeword

Linear Block Code
• In polynomial form the codeword c(x) can be written as
c(x) = m(x) g(x)
• where m(x) is the message polynomial and g(x) is the
generator polynomial, G is the generator matrix.
• G = [P | I],
• where Pi = Remainder of [xn-k+i-1/g(x)] for i=1, 2, .., k, and I
is unit matrix.
14































knkkk
kn
kn
k ppp
ppp
ppp
P
P
P
P
,21
,22221
,11211
2
1






Linear Block Code
• Example 2: Find linear block code encoder G if code
generator polynomial g(x)=1+x+x3 for a (7, 4) code.
• We have
• n = Total number of bits = 7,
• k = Number of information bits = 4,
• r = Number of parity bits = n - k = 3.
15
 













1000
0100
0010
0001
4
3
2
1
P
P
P
P
IPG 
  kiP xg
x
i
ikn
,...,2,1,ofderminRe )(
1



• Example 3: Suppose that codeword U=101110 is transmitted and
the vector r=001110 is received. That means the leftmost bit is
received in error. Find the syndrome vector value S=rHT and
verify that is equal to eHT.











001011
010110
100101
H

Error detection and error correction capabilities
• Some important terms:
• Hamming Weight or Weight of a code vector : Number of
nonzero components in codeword
• Hamming distance: Hamming distance between two
codewords is the number of components in which they
differ.
• Minimum distance: Smallest distance between any pair of
codewords in the code
 The ability of a code to detect and correct the errors can be
specified in terms of minimum distance of the code
• Theorem: The minimum distance of a LBC is equal to the
minimum weight of any nonzero codeword in the code.
• Example4: For the code in example1 find out weights of
codewords and the minimum distance of the code.
)()( VUVU,  wd

Error detection and error correction capabilities of LBC
• Theorem: A LBC with a minimum distance dmin can detect
upto dmin -1 errors and correct upto [(dmin -1)/2] errors.
 Where [(dmin -1)/2] denotes the largest integer not greater than
(dmin -1)/2.
• Proof:
 Let C be the transmitted codeword and
 R is the received codeword.
 Let C’ be the any other codeword in the code.
• Then the Hamming distance between codeword d(C,C’),
d(C,R) and d(C’,R) satisfy
d(C,R)+ d(C’,R) ≥ d(C,C’) … 1
Let the received vector consist of t errors i.e. d(C,R)=t
Let dmin be the minimum distance of the code
d(C,C’) ≥ dmin

20
• Hamming codes
 Hamming codes are a subclass of linear block codes. It
is a single error correcting perfect code.
 To correct a single error LBC must have a minimum
distance dmin =3.
 The LBC code for which t=1 and dmin=3 is called
Hamming code.
 Hamming codes have following attributes
 Hamming Codes are simple to construct
Hamming codes
t
mk
n
m
m
1:capabilitycorrectionError
3d:distanceMinimum
12:bitsninformatioofNumber
12:lengthCode
3k-nm:bitsparityofnumber
min






• For a LBC code, the required no. of bits in the codeword for
the message block size k is given by
• Proof:
 Occurrence of single error in the ith bit of codeword implies that the
syndrome of received vector is equal to the ith row of HT
 Since we have n rows in HT, for the syndrome of all single errors to be
distinct, n rows of HT should be distinct.
While choosing H following points should be consider
 There should not be a row of zeros since syndrome of 0 error does not
correspond to error.
 The last n-k rows of HT must be chosen to form identity matrix
 Each rows of HT has n-k entries which implies 2n-k distinct rows out of
which we can use 2n-k -1 distinct rows
 Since matrix has n rows, for all of them to be distinct, we need
)1(log2  nkn
LBC encoder design
)1(log)1(log12 22 
nknnknnkn

• Design a LBC code with a minimum distance of 3 and a
message block size of eight bits
• N=12 satisfies the above inequality
• Need (12,8) block code
• P is 8x4 size
• The first 8 rows of HT are arbitrarily chosen such that
 All the 8 rows must be distinct
 No row is zero row
)1(log2  nkn
LBC encoder design
knxnkn
T
I
P
H









Design the (n,k) code
1. The number of codewords is 2k
2. The all-zeros vector must be one of the codewords
3. The property of closure must apply. The sum of any two
codewords in the space must yield a valid codeword in the
space
4. Each codeword is n bits long
5. Since , the weight of each codeword must also
be at least
6. Assume the code is systematic, and the rightmost k bits of
each codeword are the corresponding message bits.
12
2 1
min




k
k
n
d

24
• Example: For a (6,3) code, the generator matrix
 Find the codewords corresponding to each distinct
messages
 Verify that this code is a single error correcting code
 Draw the encoder circuit
 Determine the syndrome vector for the received vector
r=101101. determine the corresponding data word
 Realize the syndrome encoder circuit
LBC encoder and Decoder
2
1
1
1
0
1
0
1
0
1
1
0
0
0
1
0
0
0
1
min 










 dG
 PIk :G  kn
T
IPH  : 






kn
T
I
P
H











0
1
1
1
0
1
1
1
0
1
0
0
0
1
0
0
0
1
G

25
Linear block codes – Syndrome decoding
111010001
100100000
010010000
001001000
110000100
011000010
101000001
000000000
(101011)(001000)(100011)ˆˆ
estimatedisvectorcorrectedThe
(001000)ˆ
issyndromethistoingcorrespondpatternError
(110)(100011)
:computedisofsyndromeThe
received.is(100011)




er
e
HrHS
r
r
C
TT
Error pattern Syndrome

Example:
• Consider a systematic linear block codeword whose
parity-check equations are
p1=m1+m2+m4, p2=m1+m3+m4, p3=m1+m2+m3,
p4=m2+m3+m4
where mi are message digits and pi are check digits.
(a) Find the parity-check matrix and the generator matrix
for this code.
(b) Is the vector 10101010 a codeword?
(c) How many errors can the code correct?

Cyclic Codes
• Cyclic codes form subclass of linear block codes
• Implementation of LBC is relatively simple for single error
correction. However it is too dificult for higher order error
corrections.
• Cyclic code has a simple mathematical structure that
permits design of higher order error correcting codes
• The encoder can be realized by simply using shift registers.
• A binary code is said to be cyclic if it exhibits the two
following properties
 the sum of any two code words in the code is also a code
word (linearity)
 any cyclic shift of a code word in the code is also a code
word (cyclic)

Cyclic Codes
• In Cyclic codes the codewords in the code set are simple
lateral shifts of one another such that
• Where denotes cyclic shift of C by i places to the left.
• Cyclic codes are described in a polinomial form
• This polinomial representation of cyclidc codes is useful in
analysis and implementation of the code
• code vector can be expressed as the (n-1)
degree polynomial
),,,...,,(
),...,,(
2121
)(
21
inii
i
n
ccccccCthen
cccCif


)(i
C
),...,,( 21 ncccC 

Cyclic Codes
• In polynomial form the code vector can be
represented as
• One of the interesting property of the code polynomial is that
when is devided by , the reminder is
1
1
1
11
1
201
1
1
110
...)(
...)(
...)(











n
i
n
ininin
i
n
nn
n
n
xcxcxccxc
xcxccxc
xcxccxc

),...,,,( 210 nccccC 
)(xcxi
1n
x )(xci
n
n xcxcxcxxc 1
2
10 ...)( 

Cyclic Codes
• Theorem: if g(x) is a polynomial of degree (n-k) and is a
factor of xn+1, then g(x) generates an (n,k) cyclic code
for which the code polynomial can be generated as
• This is the nonsystematic form of cyclic code
 )(1
xc
kn
kn
k
k
xgxdxggand
xdxdxddxdwhere








2
110
1
1
2
110
g(x)
)(
1
1
2
2
101
11
11
1
2
2
10









n
nn
n
nn
n
n
n
n
n
n
xcxcxcc
xcc
cxcxcxcxcx


 )1(
)()(
)(
Rem)(
)()1)(()(



n
i
x
xcxi
ini
xc
xcxxqxcx
)()()( xgxdxc 

Cyclic Code: Systematic form
• In a systematic code, the first (or last) k digits are data bits
and the last (or first) n-k digits are parity bits
• Where r(x) is a parity check polynomial
• For a systematic cyclic code, the codeword polynomial c(x)
correponding to data polynomial d(x) is given by
• Example: Construct a systematic and nonsystematic (7,4)
cyclic code using a generator polynomial for
a data vector d=1010










)(
)(
Re)(
)()()(
xg
xdx
mxrwhere
xrxdxxc
kn
kn
32
1)( xxxg 
),...,,,,...,,(),...,,,( 110110210  kknn dddrrrccccC

Cyclic Code: Symmetric form
• Given
• Systematic code is expressed as
• Nonsystematic code
1001010C
.0.1.0.1.0.0.11
1)1()(
1
)(
)(
Re)(
)()()(
6543253
23
3










 
xxxxxxxx
xxxc
xg
xdx
mxrwhere
xrxdxxc kn
2
32
1)(
1)(
xxd
xxxg


1001010C
1
)1)(1(
)()()(
543
322




xxx
xxx
xgxdxc

Generator Matrix of Cyclic Code
• Cyclic code can also be described by generator matrix
• Where the parity matrix P is determined as
• Example: determine the generator matrix for a (7,4) cyclic
code with generator polynomial
























)(
Reofrow
)(
Reofrow2
)(
Reofrow1
2
1
xg
x
mPkth
xg
x
mPnd
xg
x
mPst
kn
n
n

 kkknknk IPG   )(
1)( 23
 xxxg

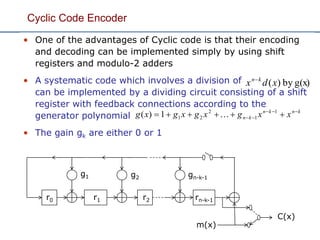
Cyclic Code Encoder
• One of the advantages of Cyclic code is that their encoding
and decoding can be implemented simply by using shift
registers and modulo-2 adders
• A systematic code which involves a division of
can be implemented by a dividing circuit consisting of a shift
register with feedback connections according to the
generator polynomial
• The gain gk are either 0 or 1
knkn
kn xxgxgxgxg 
  1
1
2
211)( 
g(x)by)(xdx kn
r0 r1 r2
gn-k-1g2
g1
rn-k-1
m(x)
C(x)

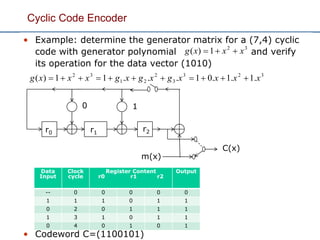
Cyclic Code Encoder
• Example: determine the generator matrix for a (7,4) cyclic
code with generator polynomial and verify
its operation for the data vector (1010)
• Codeword C=(1100101)
323
3
2
21
32
.1.1.01...11)( xxxxgxgxgxxxg 
Data
Input
Clock
cycle
Register Content
r0 r1 r2
Output
-- 0 0 0 0 0
1 1 1 0 1 1
0 2 0 1 1 1
1 3 1 0 1 1
0 4 0 1 0 1
32
1)( xxxg 
r2
10
m(x)
C(x)
r0 r1

Cyclic Code Decoder
• Every valid codeword polynomial c(x) is a multiple of g(x)
• If an error occures during the transmission,the received code
polynomial r(x) will not be a multiple of g(x), then
• s(x) is a syndrome polynomial and has a degree n-k-1 or less
• If e(x) is the code polynomial then r(x)=c(x)+e(x)
g(x)
r(x)
Rems(x)
g(x)
s(x)
)(
g(x)
r(x)


where
xm











 








)(
)(
Re
)(
)()(
Re
)(
)(
Re)(
xg
xe
m
xg
xexc
m
xg
xr
mxs

Cyclic Codes
• The polynomial plays major role in the generation of cyclic codes
• If we have a generator polynomial g(x) of an (n,k) cyclic code
with certain k polynomials, we can create the generator matrix
(G)
• Syndrome polynomial of the received code word corresponds
error polynomial
• Other remarkable cyclic codes are
 Cyclic redundancy check (CRC) codes
 Bose-Chaudhuri-Hocquenghem (BCH) codes
 Reed-Solomon codes

Digital Communication: Channel Coding

More Related Content

What's hot (20)

Similar to Digital Communication: Channel Coding (20)

More from Dr. Sanjay M. Gulhane (6)

Recently uploaded (20)

Digital Communication: Channel Coding