Dynamic Itemset Counting
Download as PPTX, PDF•17 likes•21,230 views
Dynamic Itemset Counting (DIC) is an algorithm for efficiently mining frequent itemsets from transactional data that improves upon the Apriori algorithm. DIC allows itemsets to begin being counted as soon as it is suspected they may be frequent, rather than waiting until the end of each pass like Apriori. DIC uses different markings like solid/dashed boxes and circles to track the counting status of itemsets. It can generate frequent itemsets and association rules using conviction in fewer passes over the data compared to Apriori.
Dynamic Itemset Counting
- 1. Dynamic Itemset Countingand implication Rulesfor Market Basket DataPresented bySasineePruekprasert 48052112ThatchapholSaranurak 49050511TaratDiloksawatdikul 49051006PanasSuntornpaiboolkul 49051113Department of Computer Engineering, Kasetsart University
- 2. AuthorsShalom TsurSergey BrinRajeev MotwaniJeffrey D. Ullman
- 3. The ProblemThe “market-basket” problem.Given a set of items and a large collection of transcations which are subsets (baskets) of these items.What is the relationships between the presence of various items within those baskets?
- 4. Mining Association RulesFrequent itemset generation AprioriImplication rules generation by a “threshold” ConfidenceThe Confidence of Milk Beer = δ(Milk,Beer) δ(Milk)
- 5. What does this paper do?Frequent itemset generation.AprioriImplication rules generation by a “threshold”.ConfidenceDynamic Itemset Counting(DIC)ConvictionWe will mention it first
- 6. Implication RuleTraditional methods use ConfidentSupportorInterest
- 7. Implication RuleC = δ(Milk,Beer) δ(Milk)Ignores δ(Beer) !δ(Milk,Beer) = 1 !δ(Milk)ConfidentSupportorC = δ(Milk,Beer) δ(Milk) δ(Beer)Completely Symetric!More likes co-occurrence, not implicationInterest
- 8. Implication RuleA Better Threshold!ConvictionSupportNotice that AB = ⌐ (A ∧⌐B)C = δ(Milk) δ(⌐Beer) δ(Milk, ⌐ Beer)Conviction is truly a measure of Implication!
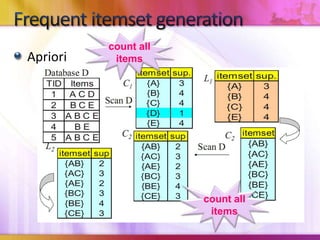
- 9. Frequent itemset generationcount all itemsAprioricount all items
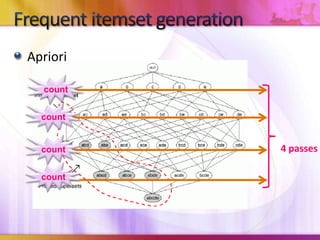
- 10. Aprioricountcountcount4 passescountFrequent itemset generation
- 11. Frequent itemset generationABcountABcountWhy do we have to wait til the end of the pass?DIC allows us to start counting an itemset as soon as we suspect it may be necessary to count it.count4 passescount
- 12. Dynamic Itemset Counting(DIC)For example: Input: 50,000 transactionsGiven constant M = 10,0001-itemsets2-itemsets3-itemsets4-itemsets< 2 passes
- 13. Apriori vs DIC1-itemsets2-itemsets3-itemsets4-itemsets4 passes< 2 passesAprioriDIC
- 14. DIC AlgorithmItemsets are marked in 4 different ways : Solid box: confirmed large itemsetSolid circle: confirmed small itemsetDashed box: suspected large itemsetDashed circle: suspected small itemset
- 15. Pseudocode AlgorithmSS = φ // solid square (frequent)SC = φ // solid circle (infrequent)DS = φ // dashed square (suspected frequent)DC = { all 1-itemsets } // dashed circle (suspected infrequent)while (DS != 0) or (DC != 0) do begin read M transactions from database into Tforall transactions t ЄT do begin // increment the respective counters of the itemsets marked with dash for each itemset c in DS or DC do begin if ( c Є t ) thenc.counter++ ;
- 16. Pseudocode Algorithm for each itemset c in DC if ( c.counter ≥ threshold ) then move c from DC to DS ; if ( any immediate superset sc of c has all of its subsets in SS or DS ) then add a new itemset sc in DC ; end for each itemset c in DS if ( c has been counted through all transactions ) then move it into SS ; for each itemset c in DC if ( c has been counted through all transactions ) then move it into SC ; endendAnswer = { c Є SS } ;
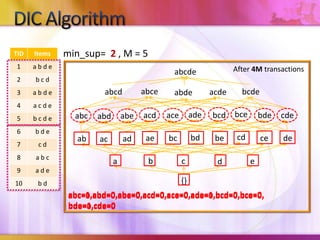
- 17. DIC Algorithmmin_sup= 2 (=20%) , M = 5
- 18. DIC AlgorithmStart of DIC algorithmabcdeabcebcdeabcdacdeabdebceadebcdacdacebdecdeabcabeabdcdbdbeaebccedeabadacbcead{}a=0, b=0, c=0, d=0, e=0Mark the empty itemset with a solid square. Mark all the 1-itemsets with dashed circles.Leave all other itemsets unmarked.
- 19. DIC AlgorithmWhile any dashed itemsets remain: 1. Read M transactions. For each transaction, increment the respective counters for the itemsets that appear in the transaction and are marked with dashes.min_sup= 2, M = 5After M transactionsabcdeabcebcdeabcdacdeabdebceadebcdacdacebdecdeabcabeabdcdbdbeaebccedeabadacbcead{}a=3, b=3, c=3, d=5, e=4
- 20. DIC Algorithm 2. If a dashed circle's count exceeds minsupp, turn it into a dashed square. If any immediate superset of it has all of its subsets as solid or dashed squares, add a new counter for it and make it a dashed circle.min_sup= 2, M = 5After M transactionsabcdeabcebcdeabcdacdeabdebceadebcdacdacebdecdeabcabeabdcdbdbeaebccedeabadacbcead{}a=3,b=3,c=3,d=5,e=4,ab=0,ac=0,ad=0,…,de=0
- 21. DIC Algorithm 3. If a dashed itemset has been counted through all the transactions, make it solid and stop counting it.min_sup= 2, M = 5After 2M transactionsabcdeabcebcdeabcdacdeabdebceadebcdacdacebdecdeabcabeabdcdbdbeaebccedeabadacbcead{}a=3+2=5, b=3+3=6, c=3+2=5, d=5+4=9, e=4+2=6,ab=1,ac=1,ad=1,ae=1,bc=1,bd=2,be=1,cd=1,ce=0,de=2a=3,b=3,c=3,d=5,e=4,ab=0,ac=0,ad=0,…,de=0
- 22. DIC Algorithm 4. If we are at the end of the transaction file, rewind to the beginning. 5. If any dashed itemsets remain, go to step 1min_sup= 2, M = 5After 3M transactionsabcdeabcebcdeabcdacdeabdebceadebcdacdacebdecdeabcabeabdcdbdbeaebccedeabadacbcead{}ab=3,ac=2,ad=4,ae=4,bc=3,bd=5,be=4,cd=4,ce=2,de=6ab=1,ac=1,ad=1,ae=1,bc=1,bd=2,be=1,cd=1,ce=1,de=2, abc=0,abd=0,abe=0,…,cde=0
- 23. DIC Algorithmmin_sup= 2, M = 5After 4M transactionsabcdeabcebcdeabcdacdeabdebceadebcdaceacdbdecdeabcabeabdcdbdbeaebccedeabadacbcead{}abc=1,abd=0,abe=0,acd=0,ace=0,ade=1,bcd=0,bce=0,bde=1,cde=0abc=0,abd=0,abe=0,acd=0,ace=0,ade=0,bcd=0,bce=0,bde=0,cde=0
- 24. DIC Algorithmmin_sup= 2, M = 5After 5M transactionsabcdeabcebcdeabcdacdeabdebceadebcdaceacdbdecdeabcabeabdcdbdbeaebccedeabadacbcead{}abc=1,abd=2,abe=2,acd=1,ace=1,ade=4,bcd=2,bce=0,bde=3,cde=2abc=1,abd=0,abe=0,acd=0,ace=0,ade=1,bcd=0,bce=0,bde=1,cde=0, abde=0
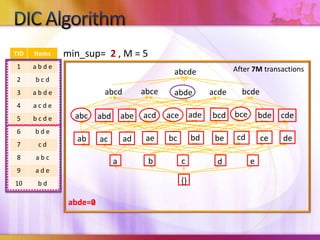
- 25. DIC Algorithmmin_sup= 2, M = 5After 6M transactionsabcdeabcebcdeabcdacdeabdebceadebcdaceacdbdecdeabcabeabdcdbdbeaebccedeabadacbcead{}abc=1,abd=2,abe=2,acd=1,ace=1,ade=4,bcd=2,bce=0,bde=3,cde=2, abde=0abde=0
- 26. DIC Algorithmmin_sup= 2, M = 5After 7M transactionsabcdeabcebcdeabcdacdeabdebceadebcdaceacdbdecdeabcabeabdcdbdbeaebccedeabadacbcead{}abde=0abde=2
- 27. Non-homogeneous DataIf data is non-homogeneous, efficiency is tend to be decreased.New item-sets for counting may come late.With greater distribution, start count AB here.Start count AB Here
- 28. Homogeneous DataSolution : randomness.Randomize order of how to read transactions.Every pass must be the same order.It may be expensive to do.
- 29. Data structure : TriesUse tries for counting item-set.Every node has counter.The order of item-set affects efficiencyThere is detail about how to reorder item-set in each transaction in paper.
- 31. Divide the database among the nodes and to have each node count all the itemsets for its own data segmentDIC can dynamically incorporate new itemsets to be added, it is not necessary to wait.Nodes can proceed to count the itemsets they suspect are candidates and make adjustments as they get more results from other nodesParallelism
- 32. Handling incremental updates involves two things: detecting when a large itemset becomes small and detecting when a small itemset becomes large.If a small itemset becomes large .We must count over the entire data, not just the update. Therefore, when we determine that a new itemset must be counted. we must go back and count it over the prefix of the data that we missed.Incremental Updates
- 33. Incremental UpdatesOldDatastartUpdatedDataDetect found Updated Datamust be counted
- 34. ReferencesBrin, Sergey and Motwani, Rajeev and Ullman, Jeffrey D. and Tsur, Shalom, Dynamic Itemset Counting and Implication Rules for Market Basket Data: Project Final Report, 1997. http://www2.cs.uregina.ca/~dbd/cs831/notes/itemsets/DIC.html
- 35. Q&A