![The Poynting vector S Definition (for free space) : S = E x H = H (-d B /dt) - E ( j f + d D /dt) Apply Divergence Theorem to integrate over wave surface A: S = energy outflux per m 2 = Intensity [W/m 2 ] S = ( E H ) = H ( E ) - E ( H ) = { Change in Electro- magnetic field energy { Joule heating losses [J/s] { Outflux of energy [J/s] = [W] Direction of S : // k E H k S](https://image.slidesharecdn.com/em-fields-slides-100804120016-phpapp02/85/Electromagnetic-fields-10-320.jpg)
Electromagnetic fields
- 1. Electromagnetism University of Twente Department Applied Physics First-year course on Part III: Electromagnetic Waves : Slides © F.F.M. de Mul
- 2. Electromagnetic Waves Gauss’ and Faraday’s Laws for E ( D ) - field Gauss’ and Maxwell’s Laws for B ( H )-field Maxwell’s Equations and The Wave Equation Harmonic Solution of the Wave Equation Plane waves (1): orientation of field vectors Plane waves (2): complex wave vector Plane waves (3): the B - E correspondence The Poynting Vector
- 3. Gauss’ and Faraday’s Laws for E Div = micro-flux per unit of volume Rot = micro-circulation per unit of area B c dS Faraday’s Law : S E S V dV Gauss’ Law :
- 4. Gauss’ and Maxwell’s Law for B S V dV B Gauss’ Law : j S L Maxwell’s Fix for Ampere’s Law :
- 5. Maxwell’s Equations and the Wave Equation This is a 3-Dimensional Wave Equation v = 2.99… x 10 8 m/s = light velocity In vacuum ( = 0 and j = 0): }
- 6. Harmonic Solution of the Wave Equation: Plane Waves E may have 3 components: E x E y E z Choose x-axis // E E y = E z = 0 (Polarization direction = x-axis). Does a plane-wave expression for E x satisfy the wave equation? E x = E x0 exp{ i ( t-kz )} : E x0 = amplitude + polarization vector +z-axis = direction of propagation Insertion into wave equation: k 2 = 0 0 2 = 2 / c 2 k = / c = 2 / k = wave number ; = wavelength (in 3D-case: k = wave vector ) Analogously: B y = B y0 exp{ i ( t-kz )}
- 7. Plane waves (1): orientation of fields -i k e z .E = 0 -i k e z .H = 0 -i k e z x E = -i H -i k e z x H = E +i E (1) div E = 0 (2) div B = 0 (3) rot E = - d B/ dt (4) rot H = j f + d D /dt j f = E Consequences: (1)+(2): E and H e z (3)+(4): E H If E chosen // x-axis, then H // y-axis Suppose : E // x-axis; .. propagation // +z-axis: k // e z .. E x = E x0 exp i ( t-kz ) x z y E Propag- ation H
- 8. Plane waves (2): complex wave vector e z x e z x E = -E i k 2 = ( + i ). Result: k complex: k = k Re + i k Im exp (-i kz ) = exp (-i k Re z ) . exp ( k Im z ) (1) -i k e z .E = 0 (2) -i k e z .H = 0 (3) -i k e z x E = -i H (4) -i k e z x H = E +i E (1)+(2): E and H e z (3)+(4): E H Suppose : E // x-axis; .. propagation // +z-axis: k // e z .. E x = E x0 exp i ( t-kz ) x z y E Propag- ation H } harmonic } k Im < 0 : absorption >0 : amplification (“laser”)
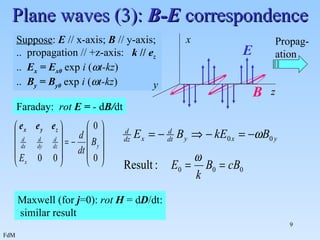
- 9. Plane waves (3): B-E correspondence Faraday: rot E = - d B/ dt Maxwell (for j =0): rot H = d D /dt: similar result Suppose : E // x-axis; B // y-axis; .. propagation // +z-axis: k // e z .. E x = E x0 exp i ( t-kz ) .. B y = B y0 exp i ( t-kz ) x z y E Propag- ation B
- 10. The Poynting vector S Definition (for free space) : S = E x H = H (-d B /dt) - E ( j f + d D /dt) Apply Divergence Theorem to integrate over wave surface A: S = energy outflux per m 2 = Intensity [W/m 2 ] S = ( E H ) = H ( E ) - E ( H ) = { Change in Electro- magnetic field energy { Joule heating losses [J/s] { Outflux of energy [J/s] = [W] Direction of S : // k E H k S