![error
1
Models Previous work
– and algorithms for high performance !
from the PI tackled net- computations
matrix and network
FIGURE 6
std
2
work alignment with matrix methods =for cm
edge
(b) Std, s 0.39
Simulation data analysis
overlap:
SIMAX ‘09, SISC ‘11,MapReduce ‘11, ICASSP ’12
1
j
i
i0
Overlap
Overlap
j0
error
SC ‘05, WAW ‘07, SISC ‘10, WWW ’10, …
Massive matrix "
computations
std
0
0
Fast & Scalable"
Network centrality
0
20
10
10
A
L
B
Tensor eigenvalues"
0
(d) Std, s = 1.95 cm
Ax = b
min kAx bk
Ax = x
This proposal is for matchand a power method
Network alignment
tensor
ing triangles using
P
methods:
on multi-threaded
maximize
Tijk xi xj xk
model compared to the prediction standard debble locations at the final time for two values of
ICDM ‘09, SC ‘11, TKDE ‘13
= 1.95 cm. (Colors are visible in the electronic
ijk
n
and kxk2 = 1
subject to distributed
j
Triangle
j
X
i
s
i
approximately twenty minutes to construct using (next) architectures
k
[x
]i = ⇢ · (
Tijk xj xk + xi )
k
s.
jk
s- involved a few pre- and post-processing steps:
ta
where ! ensures the 2-norm
m Aria, globally transpose the data, compute the
g errors. The preprocessing steps took approx- SSHOPM method due to "
nd
0
0
Data clustering
WSDM ‘12, KDD ‘12, CIKM ’13 …
0
A
recise timing information, L we do notB
but
report
David
Kolda and Mayo
Gleich
· Purdue
Mines
2
t
r
o
s.
g
n.
o](https://image.slidesharecdn.com/nexpokit-mines-140208091610-phpapp02/85/Fast-relaxation-methods-for-the-matrix-exponential-2-320.jpg)
![Matrix exponentials on large networks
1
X 1
exp(A) =
Ak
k!
k =0
If A is the adjacency matrix, then
Ak counts the number of length k
paths between node pairs.
[Estrada 2000, Farahat et al. 2002, 2006]
Large entries denote important nodes or edges.
Used for link prediction and centrality
k =0
If P is a transition matrix, then "
Pk is the probability of a length k
walk between node pairs.
[Kondor & Lafferty 2002, Kunegis & Lommatzsch 2009, Chung 2007]
Used for link prediction, kernels, and
clustering or community detection
David Gleich · Purdue
Mines
13
1
X 1
exp(P) =
Pk
k!](https://image.slidesharecdn.com/nexpokit-mines-140208091610-phpapp02/85/Fast-relaxation-methods-for-the-matrix-exponential-13-320.jpg)
![The issue with existing methods
We want good results in less than one matvec.
Our graphs have small diameter and fast fill-in.
Krylov methods !
exp(P)ec ⇡ ⇢Vexp(H)e1
[Sidje 1998]"
ExpoKit
A few matvecs, quick loss of sparsity due to orthogonality
!
Direct expansion! exp(P)ec ⇡
PN
1 k
k =0 k ! P ec
David Gleich · Purdue
Mines
18
A few matvecs, quick loss of sparsity due to fill-in](https://image.slidesharecdn.com/nexpokit-mines-140208091610-phpapp02/85/Fast-relaxation-methods-for-the-matrix-exponential-18-320.jpg)
![Justification of terminology
This method is frequently “rediscovered” (3 times for PageRank!)
Let Ax = b, diag(A) = I
It’s Gauss-Seidel if j is chosen cyclically
It’s Gauss-Southwell if j is the largest entry in the residual
It’s coordinate descent if A is symmetric, pos. definite
It’s a relaxation step for any A
David Gleich · Purdue
Mines
28
Works great for other problems too! "
[Bonchi, Gleich, et al. J. Internet Math. 2012]](https://image.slidesharecdn.com/nexpokit-mines-140208091610-phpapp02/85/Fast-relaxation-methods-for-the-matrix-exponential-28-320.jpg)
![Code (inefficient, but working) for !
Gauss-Southwell to solve
function x = nexpm(P,c,tol)
n = size(P,1); N = 11; sumr=1;
r = zeros(n,N+1); r(c,1) = 1; x = zeros(n,1); % the residual and solution
while sumr >= tol % use max iteration too
[ml,q]=max(r(:)); i=mod(q-1,n)+1; k=ceil(q/n); % use a heap in practice for max
r(q) = 0; x(i) = x(i)+ml; sumr = sumr-ml;% zero the residual, add to solution
[nset,~,vals] = find(P(:,i)); ml=ml/k; % look up the neighbors of node i
for j=1:numel(nset) % for all neighbors
if k==N, x(nset(j)) = x(nset(j)) + vals(j)*ml; % add to solution
else, r(nset(j),k+1) = r(nset(j),k+1) + vals(j)*ml;% or add to next residual
sumr = sumr + vals(j)*ml;
end, end, end % end if, end for, end while
David Gleich · Purdue
Mines
30
Todo use dictionary for x, r and use heap or queue for residual](https://image.slidesharecdn.com/nexpokit-mines-140208091610-phpapp02/85/Fast-relaxation-methods-for-the-matrix-exponential-30-320.jpg)
Fast relaxation methods for the matrix exponential
- 1. Relaxation methods for ! the matrix exponential ! on large networks Code www.cs.purdue.edu/homes/dgleich/codes/nexpokit! David F. Gleich! Purdue University! David Gleich · Purdue Mines 1 Joint work with Kyle Kloster @ Purdue supported by " NSF CAREER 1149756-CCF
- 2. error 1 Models Previous work – and algorithms for high performance ! from the PI tackled net- computations matrix and network FIGURE 6 std 2 work alignment with matrix methods =for cm edge (b) Std, s 0.39 Simulation data analysis overlap: SIMAX ‘09, SISC ‘11,MapReduce ‘11, ICASSP ’12 1 j i i0 Overlap Overlap j0 error SC ‘05, WAW ‘07, SISC ‘10, WWW ’10, … Massive matrix " computations std 0 0 Fast & Scalable" Network centrality 0 20 10 10 A L B Tensor eigenvalues" 0 (d) Std, s = 1.95 cm Ax = b min kAx bk Ax = x This proposal is for matchand a power method Network alignment tensor ing triangles using P methods: on multi-threaded maximize Tijk xi xj xk model compared to the prediction standard debble locations at the final time for two values of ICDM ‘09, SC ‘11, TKDE ‘13 = 1.95 cm. (Colors are visible in the electronic ijk n and kxk2 = 1 subject to distributed j Triangle j X i s i approximately twenty minutes to construct using (next) architectures k [x ]i = ⇢ · ( Tijk xj xk + xi ) k s. jk s- involved a few pre- and post-processing steps: ta where ! ensures the 2-norm m Aria, globally transpose the data, compute the g errors. The preprocessing steps took approx- SSHOPM method due to " nd 0 0 Data clustering WSDM ‘12, KDD ‘12, CIKM ’13 … 0 A recise timing information, L we do notB but report David Kolda and Mayo Gleich · Purdue Mines 2 t r o s. g n. o
- 3. The talk ends, you believe -- whatever you want to. Image from rockysprings, deviantart, CC share-alike 3 Everything in the world can be explained by a matrix, and we see how deep the rabbit hole goes
- 4. Matrix exponentials A is n ⇥ n, real 1 X 1 exp(A) is defined as Ak k! Always converges k =0 dx = Ax(t) dt , x(t) = exp(tA)x(0) Evolution operator " for an ODE David Gleich · Purdue Mines 4 special case of a function of a matrix f (A) others are f (x) = 1/x; f (x) = sinh(x)...
- 5. This talk: a column of the matrix exponential x = exp(P)ec x the solution P the matrix the column David Gleich · Purdue Mines 5 ec
- 6. Matrix computations in a red-pill David Gleich · Purdue Mines 6 Solve a problem better by exploiting its structure!
- 7. This talk: a column of the matrix exponential x = exp(P)ec the solution localized P the matrix large, sparse, stochastic x the column David Gleich · Purdue Mines 7 ec
- 8. Localized solutions x = exp(P)ec nnz(x) = 513, 969 plot(x) 1.5 10 1 10 0 error −5 0.5 −15 0 2 4 6 5 x 10 length(x) = 513, 969 10 0 10 2 10 4 10 6 10 nonzeros David Gleich · Purdue Mines 8 0 −10 10
- 9. Our mission! David Gleich · Purdue Mines 9 Find the solution with work " roughly proportional to the " localization, not the matrix.
- 10. Our algorithm! www.cs.purdue.edu/homes/dgleich/codes/nexpokit 0 10 −5 error 10 −10 10 −15 0 10 2 4 10 10 6 10 nonzeros David Gleich · Purdue Mines 10 10
- 11. Outline 1. Motivation and setup 2. Converting x = exp(P) ec into a linear system 3. Relaxation methods for " linear systems from large networks 4. Error analysis David Gleich · Purdue Mines 11 5. Experiments
- 12. SIAM REVIEW Vol. 45, No. 1, pp. 3–49 c ⃝ 2003 Society for Industrial and Applied Mathematics Cleve Moler† Charles Van Loan‡ David Gleich · Purdue Mines 12 Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later∗
- 13. Matrix exponentials on large networks 1 X 1 exp(A) = Ak k! k =0 If A is the adjacency matrix, then Ak counts the number of length k paths between node pairs. [Estrada 2000, Farahat et al. 2002, 2006] Large entries denote important nodes or edges. Used for link prediction and centrality k =0 If P is a transition matrix, then " Pk is the probability of a length k walk between node pairs. [Kondor & Lafferty 2002, Kunegis & Lommatzsch 2009, Chung 2007] Used for link prediction, kernels, and clustering or community detection David Gleich · Purdue Mines 13 1 X 1 exp(P) = Pk k!
- 14. Another useful matrix exponential P column stochastic e.g. P = AT D 1 A is the adjacency matrix if A is symmetric 1 A) = D 1 exp(AD 1 )D = D David Gleich · Purdue 1 exp(P)D Mines 14 exp(PT ) = exp(D
- 15. Another useful matrix exponential P column stochastic e.g. P = AT D 1 A is the adjacency matrix heat kernel of a graph dx(t) = Lx(t) dt solves the heat equation at t=1. exp( L) = exp(D 1/2 AD 1/2 I) Negative Normalized Laplacian 1 = exp(D 1/2 AD 1/2 ) e 1 1/2 1 1/2 1 1/2 = D exp(AD )D = D exp(P)D1/2 e e David Gleich · Purdue Mines 15 if A is symmetric
- 16. Matrix exponentials on large networks Is a single column interesting? Yes! 1 X 1 exp(P)ec = Pk ec k! k =0 Link prediction scores for node c A community relative to node c But … and so we’d like " speed over accuracy David Gleich · Purdue Mines 16 modern networks are " large ~ O(109) nodes, sparse ~ O(1011) edges, constantly changing …
- 17. Newman’s netscience collaboration network! 379 vertices 1828 non-zeros x = exp(P)ec “zero” on most nodes David Gleich · Purdue Mines 17 ec has a single " one here
- 18. The issue with existing methods We want good results in less than one matvec. Our graphs have small diameter and fast fill-in. Krylov methods ! exp(P)ec ⇡ ⇢Vexp(H)e1 [Sidje 1998]" ExpoKit A few matvecs, quick loss of sparsity due to orthogonality ! Direct expansion! exp(P)ec ⇡ PN 1 k k =0 k ! P ec David Gleich · Purdue Mines 18 A few matvecs, quick loss of sparsity due to fill-in
- 19. Outline 1. Motivation and setup ✓ 2. Converting x = exp(P) ec into a linear system 3. Relaxation methods for " linear systems from large networks 4. Error analysis David Gleich · Purdue Mines 19 5. Experiments
- 20. Our underlying method Direct expansion! x = exp(P)ec ⇡ PN 1 k k =0 k ! P ec = xN A few matvecs, quick loss of sparsity due to fill-in This method is stable for stochastic P! "… no cancellation, unbounded norm, etc. ! Lemma kx 1 xN k1 N!N David Gleich · Purdue Mines 20 !
- 21. Our underlying method ! as a linear system Direct expansion! x = exp(P)ec 2 I 6 P/1 I 6 6 .. 6 . P/2 " 6 6 .. ! 4 . I P/N I ! ! I (I ⌦ I N PN ⇡ 32 1 k k =0 k ! P ec = xN 3 2 3 v0 ec 7 6 v1 7 6 0 7 76 7 6 7 N X 76 . 7 6 . 7 7 6 . 7 = 6 . 7 xN = vi 76 . 7 6 . 7 76 . 7 6 . 7 i=0 54 . 5 4 . 5 . . vN 0 SN ⌦ P)v = e1 ⌦ ec David Gleich · Purdue Mines 21 Lemma we approximate xN well if we approximate v well
- 22. Our mission (2)! Approximately solve " Ax = b David Gleich · Purdue Mines 22 when A, b are sparse," x is localized.
- 23. Outline 1. Motivation and setup ✓ ✓ 2. Converting x = exp(P) ec into a linear system 3. Relaxation methods for " linear systems from large networks 4. Error analysis David Gleich · Purdue Mines 23 5. Experiments
- 24. Coordinate descent, Gauss-Southwell, Gauss-Seidel, relaxation & “push” methods Be greedy Don’t look at the whole system. David Gleich · Purdue Mines 24 Look at equations that are violated and try and fix them.
- 25. Coordinate descent, Gauss-Southwell, Gauss-Seidel, relaxation & “push” methods Ax = b r(k) = b Ax(k) x(k +1) = x(k ) + ej eT r(k ) j r(k +1) = r(k) rj(k) Aej Procedurally! Solve(A,b) x = sparse(size(A,1),1) r = b While (1) Pick j where r(j) != 0 z = r(j) x(j) = x(j) + r(j) For i where A(i,j) != 0 r(i) = r(i) – z*A(i,j) David Gleich · Purdue Mines 25 Algebraically!
- 26. It’s called the “push” method because of PageRank r(k) = v ↵P)x = v I (I PageRankPush(links,v,alpha) ↵P)x(k) x(k +1) = x(k ) + ej eT r(k ) j “r(k +1) = r(k ) rj(k) Aej ” 8 >0 < ri(k +1) = ri(k) + ↵Pi,j rj(k) > (k) : ri x = sparse(size(A,1),1) r = b While (1) Pick j where r(j) != 0 z = r(j) x(j) = x(j) + z r(j) = 0 z = alpha * z / deg(j) For i where “j links to i” r(i) = r(i) + z i =j Pi,j 6= 0 otherwise David Gleich · Purdue Mines 26 I (I
- 27. It’s called the “push” method because of PageRank David Gleich · Purdue Mines 27 Demo
- 28. Justification of terminology This method is frequently “rediscovered” (3 times for PageRank!) Let Ax = b, diag(A) = I It’s Gauss-Seidel if j is chosen cyclically It’s Gauss-Southwell if j is the largest entry in the residual It’s coordinate descent if A is symmetric, pos. definite It’s a relaxation step for any A David Gleich · Purdue Mines 28 Works great for other problems too! " [Bonchi, Gleich, et al. J. Internet Math. 2012]
- 29. Back to the exponential 2 6 6 6 6 6 6 4 I P/1 I (I ⌦ I N I P/2 .. . .. . 32 I P/N 3 2 3 v0 ec 7 6 v1 7 6 0 7 76 7 6 7 N X 76 . 7 6 . 7 7 6 . 7 = 6 . 7 xN = vi 76 . 7 6 . 7 76 . 7 6 . 7 i=0 54 . 5 4 . 5 . . I vN 0 SN ⌦ P)v = e1 ⌦ ec David Gleich · Purdue Mines 29 Solve this system via the same method. Optimization 1 build system implicitly Optimization 2 don’t store vi, just store sum xN
- 30. Code (inefficient, but working) for ! Gauss-Southwell to solve function x = nexpm(P,c,tol) n = size(P,1); N = 11; sumr=1; r = zeros(n,N+1); r(c,1) = 1; x = zeros(n,1); % the residual and solution while sumr >= tol % use max iteration too [ml,q]=max(r(:)); i=mod(q-1,n)+1; k=ceil(q/n); % use a heap in practice for max r(q) = 0; x(i) = x(i)+ml; sumr = sumr-ml;% zero the residual, add to solution [nset,~,vals] = find(P(:,i)); ml=ml/k; % look up the neighbors of node i for j=1:numel(nset) % for all neighbors if k==N, x(nset(j)) = x(nset(j)) + vals(j)*ml; % add to solution else, r(nset(j),k+1) = r(nset(j),k+1) + vals(j)*ml;% or add to next residual sumr = sumr + vals(j)*ml; end, end, end % end if, end for, end while David Gleich · Purdue Mines 30 Todo use dictionary for x, r and use heap or queue for residual
- 31. Outline 1. Motivation and setup ✓ ✓ ✓ 2. Converting x = exp(P) ec into a linear system 3. Relaxation methods for " linear systems from large networks 4. Error analysis David Gleich · Purdue Mines 31 5. Experiments
- 32. Error analysis for Gauss-Southwell I (I ⌦ I N SN ⌦ P)v = e1 ⌦ ec Theorem Assume P is column-stochastic, v(0) = 0. (Nonnegativity) iterates and residuals are nonnegative v(l) 0 and r(l) 0 1 2dk l( 1 2d ) “annoying” d is the largest degree David Gleich · Purdue Mines 32 (Convergence) residual goes to 0: Ql (l) kr k1 k=1 1 “easy”
- 33. Proof sketch Gauss-Southwell picks largest residual ⇒ Bound the update by avg. nonzeros in residual (sloppy) ⇒ Algebraic convergence with slow rate, but each update is REALLY fast O(d max log n). David Gleich · Purdue Mines 33 If d is log log n, then our method runs in sub-linear time " (but so does just about anything)
- 34. Overall error analysis After ℓ steps of Gauss-Southwell Theorem kxN (`) 1 1 xk1 + ·` N!N e 1 2d David Gleich · Purdue Mines 34 Components! Truncation to N terms Residual to error Approximate solve
- 35. More recent error analysis Theorem (Gleich and Kloster, 2013 arXiv:1310.3423)" Consider solving personalized PageRank using the GaussSouthwell relaxation method in a graph with a Zipf-law in the degrees with exponent p=1 and max-degree d, then the work involved in getting a solution with 1-norm error ε is work = O log( 1 )( 1 )3/2 d 2 (log d)2 " " ⌘ David Gleich · Purdue Mines 35 ⇣
- 36. Outline 1. Motivation and setup ✓ ✓ ✓ 2. Converting x = exp(P) ec into a linear system 3. Relaxation methods for " linear systems from large networks 4. Error analysis ✓ David Gleich · Purdue Mines 36 5. Experiments
- 37. Our implementations C++ mex implementation with a heap to implement Gauss-Southwell. C++ mex implementation with a queue to store all residual entries ≥ 1/(tol nN). At completion, the residual norm ≤ tol. David Gleich · Purdue Mines 37 We use the queue except for the runtime comparison.
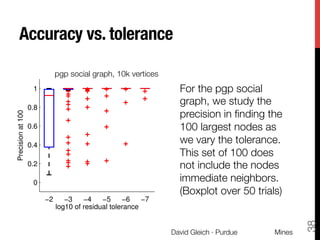
- 38. Accuracy vs. tolerance pgp−cc pgp social graph, 10k vertices 0.8 0.6 0.4 0.2 0 −2 −3 −4 −5 −6 −7 log10 of residual tolerance For the pgp social graph, we study the precision in finding the 100 largest nodes as we vary the tolerance. This set of 100 does not include the nodes immediate neighbors. (Boxplot over 50 trials) David Gleich · Purdue Mines 38 Precision at 100 1
- 39. Accuracy vs. work dblp−cc dblp collaboration graph, 225k vertices 1 0.6 tol=10−5 tol=10−4 0.4 @10 @25 0.2 @100 @1000 0 −2 −1 0 10 10 10 Effective matrix−vector products David Gleich · Purdue Mines 39 Precision 0.8 For the dblp collaboration graph, we study the precision in finding the 100 largest nodes as we vary the work. This set of 100 does not include the nodes immediate neighbors. (One column, but representative)
- 40. Runtime Flickr social network" 500k nodes, 5M edges 0 −2 10 TSGS TSGSQ EXPV MEXPV TAYLOR −4 10 3 10 4 10 5 10 |E| + |V| 6 10 David Gleich · Purdue Mines 40 Runtime (secs). 10
- 41. Outline 1. Motivation and setup ✓ ✓ ✓ 3. Coordinate descent methods for " linear systems from large networks 4. Error analysis 5. Experiments ✓ ✓ David Gleich · Purdue Mines 41 2. Converting x = exp(P) ec into a linear system
- 42. References and ongoing work Kloster and Gleich, Workshop on Algorithms for the Web-graph, 2013. Also see the journal version on arXiv. www.cs.purdue.edu/homes/dgleich/codes/nexpokit Error analysis using the queue (almost done …) • Better linear systems for faster convergence • Asynchronous coordinate descent methods • Scaling up to billion node graphs (done …) www.cs.purdue.edu/homes/dgleich Supported by NSF CAREER 1149756-CCF David Gleich · Purdue Mines 42 •