![The equivalence classes are
[0]R= {…-10, -5, 0, 5,10,…}
[1]R = {…..,-9, -4, 1, 6, 11, 16….}
[2]R= {….-8, -3,2,7,12,17…..}
[3]R = {….-7, -2, 3, 8 ,13,…}
[4]R = {….-6,-1,4,9,14,19,….}
Z/R ={[0]R, [1]R, [2]R, [3]R, [4]R}](https://image.slidesharecdn.com/finiteautomataintro-120327095453-phpapp02/85/Finite-automata-intro-19-320.jpg)
Finite automata intro
- 1. Theory of Automata & Formal Languages
- 2. BOOKS Theory of computer Science: K.L.P.Mishra & N.Chandrasekharan Intro to Automata theory, Formal languages and computation: Ullman,Hopcroft Motwani Elements of theory of computation Lewis & papadimitrou
- 3. Syllabus Introduction Deterministic and non deterministic Finite Automata, Regular Expression,Two way finite automata,Finite automata with output,properties of regular sets,pumping lemma, closure properties,Myhill nerode theorem
- 4. Context free Grammar: Derivation trees, Simplification forms Pushdown automata: Def, Relationship between PDA and context free language,Properties, decision algorithms Turing Machines: Turing machine model,Modification of turing machines,Church’s thesis,Undecidability,Recursive and recursively enumerable languages Post correspondence problems recursive functions
- 5. Chomsky Hierarchy: Regular grammars, unrestricted grammar, context sensitive language, relationship among languages
- 6. temporary memory input memory CPU output memory Program memory
- 7. 3 temporary memory f ( x) = x z = 2*2 = 4 f ( x) = z * 2 = 8 input memory x=2 CPU output memory Program memory compute x∗x 2 compute x ∗x
- 8. Automaton temporary memory Automaton input memory CPU output memory Program memory
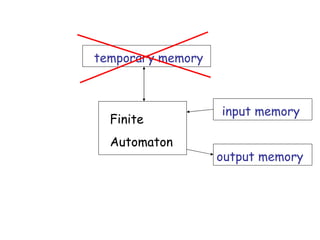
- 9. temporary memory input memory Finite Automaton output memory
- 10. Different Kinds of Automata Automata are distinguished by the temporary memory • Finite Automata: no temporary memory • Pushdown Automata: stack • Turing Machines: random access memory
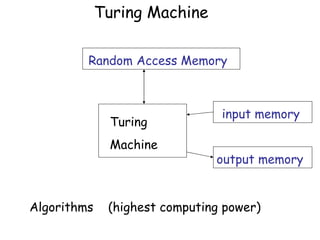
- 11. Turing Machine Random Access Memory input memory Turing Machine output memory Algorithms (highest computing power)
- 12. Power of Automata Finite Pushdown Turing Automata Automata Machine
- 13. Power sets A power set is a set of sets S = { a, b, c } Powerset of S = the set of all the subsets of S 2S = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } Observation: | 2S | = 2|S| ( 8 = 23 )
- 14. Cartesian Product A = { 2, 4 } B = { 2, 3, 5 } A X B = { (2, 2), (2, 3), (2, 5), ( 4, 2), (4, 3), (4, 4) } |A X B| = |A| |B| Generalizes to more than two sets AXBX…XZ
- 15. RELATIONS R = {(x1, y1), (x2, y2), (x3, y3), …} xi R yi e. g. if R = ‘>’: 2 > 1, 3 > 2, 3 > 1 In relations xi can be repeated
- 16. Equivalence Relations • Reflexive: xRx • Symmetric: xRy yRx • Transitive: x R Y and y R z xRz Example: R = ‘=‘ •x=x •x=y y=x • x = y and y = z x=z
- 17. Equivalence Classes For equivalence relation R equivalence class of x = {y : x R y} Example: R = { (1, 1), (2, 2), (1, 2), (2, 1), (3, 3), (4, 4), (3, 4), (4, 3) } Equivalence class of 1 = {1, 2} Equivalence class of 3 = {3, 4}
- 18. Example of Equivalence relation Let Z = set of integers R be defined on it as: R= {(x,y)| x ∈Z, y ∈ Z and (x - y)is divisible by 5} This relation is known as ” congruent modulo 5”
- 19. The equivalence classes are [0]R= {…-10, -5, 0, 5,10,…} [1]R = {…..,-9, -4, 1, 6, 11, 16….} [2]R= {….-8, -3,2,7,12,17…..} [3]R = {….-7, -2, 3, 8 ,13,…} [4]R = {….-6,-1,4,9,14,19,….} Z/R ={[0]R, [1]R, [2]R, [3]R, [4]R}
- 20. PROOF TECHNIQUES • Proof by induction • Proof by contradiction
- 21. Induction We have statements P1, P2, P3, … If we know • for some k that P1, P2, …, Pk are true • for any n >= k that P1, P2, …, Pn imply Pn+1 Then Every Pi is true
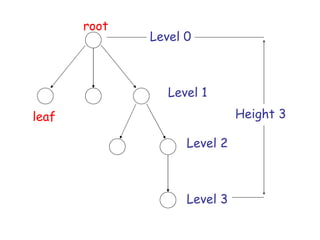
- 22. Trees root parent leaf child Trees have no cycles
- 23. Proof by Induction • Inductive basis Find P1, P2, …, Pk which are true • Inductive hypothesis Let’s assume P1, P2, …, Pn are true, for any n >= k • Inductive step Show that Pn+1 is true
- 24. root Level 0 Level 1 leaf Height 3 Level 2 Level 3
- 25. Binary Trees
- 26. Example Theorem: A binary tree of height n has at most 2n leaves. Proof: let l(i) be the number of leaves at level i l(0) = 0 l(3) = 8
- 27. Induction Step Level n hypothesis: l(n) <= 2n n+1
- 28. We want to show: l(i) <= 2i • Inductive basis l(0) = 1 (the root node) • Inductive hypothesis Let’s assume l(i) <= 2i for all i = 0, 1, …, n • Induction step we need to show that l(n + 1) <= 2n+1
- 29. Induction Step Level n hypothesis: l(n) <= 2n n+1 l(n+1) <= 2 * l(n) <= 2 * 2n = 2n+1
- 30. Proof by Contradiction We want to prove that a statement P is true • we assume that P is false • then we arrive at an incorrect conclusion • therefore, statement P must be true
- 31. Example Theorem: 2 is not rational Proof: Assume by contradiction that it is rational 2 = n/m n and m have no common factors We will show that this is impossible
- 32. 2 = n/m 2 m2 = n2 n is even Therefore, n2 is even n=2k m is even 2 m2 = 4k2 m2 = 2k2 m=2p Thus, m and n have common factor 2 Contradiction!
- 33. Basic Terms Alphabet: A finite non empty set of elements. ∑∑ ={a,b,c,d,…z}
- 34. ∑ • String: A sequence of letters – Examples: “cat”, “dog”, “house”, … – Defined over an alphabet: Σ={a, b, c,, z} Language: It is a set of strings on some alphabet
- 35. Alphabets and Strings • We will use small alphabets: • Strings Σ = { a, b} a u = ab ab v = bbbaaa abba w = abba baba aaabbbaabab
- 36. String Operations abba w = a1a2 an bbbaaa v = b1b2 bm Concatenation wv = a1a2 anb1b2 bm abbabbbaaa
- 37. w = a1a2 an ababaaabbb Reverse R w = an a2 a1 bbbaaababa
- 38. String Length w = a1a2 an w =n • Length: abba = 4 • Examples: aa = 2 a =1
- 39. Recursive Definition of Length a =1 For any letter: wa wa = w + 1 For any string : abba = abb + 1 = ab + 1 + 1 Example: = a +1+1+1 = 1+1+1+1 =4
- 40. Length of Concatenation uv = u + v u = aab, u = 3 • Example: = abaab, v v =5 uv = aababaab = 8 uv = u + v = 3 + 5 = 8
- 41. Proof of Concatenation Length uv = u + v • Claim: v • Proof: By induction on the length v =1 – Induction basis: – From definition of length: uv = u +1 = u + v
- 42. uv = u + v – Inductive hypothesis: v = 1,2,, n • for – Inductive step: we will prove uv = u + v – – for v = n +1
- 43. Inductive Step v = wa w = n, a = 1 • Write , where uv = uwa = uw + 1 • From definition of length: wa = w + 1 • From inductive hypothesis: uw = u + w • Thus: uv = u + w + 1 = u + wa = u + v
- 44. Empty String λ • A string with no letters: λ =0 • Observations: λw = wλ = w λabba = abbaλ = abba
- 45. Substring • Substring of string: – a subsequence of consecutive characters abbab ab • String Substring abbab abba abbab b abbab bbab
- 46. Prefix and Suffix • Prefixes Suffixes abbab w = uv λ abbab a bbab prefix ab bab suffix abb ab abba b abbab λ
- 47. Another Operation wn = ww w n ( abba ) = abbaabba 2 • Example: 0 • Definition: w =λ – ( abba ) = λ 0
- 48. The * Operation • Σ * : the set of all possible strings from • Σ alphabet Σ = { a, b} Σ* = { λ, a, b, aa, ab, ba, bb, aaa, aab,} •
- 49. The + Operation + : the set of all possible strings from Σ alphabet Σ except λ Σ = { a, b} Σ* = { λ , a, b, aa, ab, ba, bb, aaa, aab,} + Σ = Σ * −λ + Σ = { a, b, aa, ab, ba, bb, aaa, aab,}
- 50. Language • A language is any subset of Σ* Σ = { a, b} • Example: Σ* = { λ , a, b, aa, ab, ba, bb, aaa,} { λ} { a, aa, aab} • Languages: {λ , abba, baba, aa, ab, aaaaaa}
- 51. Another Example n n L = {a b : n ≥ 0} • An infinite language λ ab ∈L abb ∉ L aabb aaaaabbbbb
- 52. Operations on Languages • The usual set operations { a, ab, aaaa} { bb, ab} = {a, ab, bb, aaaa} { a, ab, aaaa} { bb, ab} = {ab} { a, ab, aaaa} − { bb, ab} = { a, aaaa} • Complement: L = Σ * −L { a, ba} = { λ , b, aa, ab, bb, aaa,}
- 53. Reverse R R L = {w : w ∈ L} • Definition: • { ab, aab, baba} = { ba, baa, abab} Examples: R n n L = {a b : n ≥ 0} R n n L = {b a : n ≥ 0}
- 54. Concatenation L1L2 = { xy : x ∈ L1, y ∈ L2 } • Definition: { a, ab, ba}{ b, aa} • Example: = { ab, aaa, abb, abaa, bab, baaa}
- 55. Another Operation Ln = LL L n • Definition: { a, b}3 ={ a, b}{ a, b}{ a, b} = { aaa, aab, aba, abb, baa, bab, bba, bbb} L0 = { λ} • Special case: 0 { a , bba , aaa } = { λ}
- 56. More Examples n n • L = {a b : n ≥ 0} 2 n n m m L = {a b a b : n, m ≥ 0} 2 aabbaaabbb ∈ L
- 57. Star-Closure (Kleene *) 0 1 2 L* = L L L • Definition: • Example: λ , a, bb, { a, bb} * = aa, abb, bba, bbbb, • aaa, aabb, abba, abbbb,
- 58. Positive Closure + 1 2 L = L L • Definition: = L * −{ λ } a, bb, + { a, bb} = aa, abb, bba, bbbb, aaa, aabb, abba, abbbb,
- 59. Finite Automaton Input • String Output Finite String Automaton