Genetic algorithm
- 1. GENETIC ALGORITHM Megha V Research Scholar Dept of IT, Kannur University Email: [email protected]
- 2. OUTLINE Introduction What are GAs? Genetic Algorithm History Basic Idea of Nature Selection. Basic Genetic Algorithm. Nature to Computer Mapping. GA Operators and Parameters: Advantages of GAs. Limitations of GAs. 2/1/2021 GENETIC ALGORITHM 2
- 3. INTRODUCTION After scientist became disillusioned with classical and nonclassical attempts at modeling intelligence , they looked in other directions. Two prominent fields arose, connectionism (neural networking, parallel processing) and evolutionary computing. Basic concept- to stimulate process in natural system necessary for evolution. 2/1/2021 GENETIC ALGORITHM 3
- 4. WHAT ARE GENETIC ALGORITHMS? Genetic Algorithm (GA) is a search-based optimization technique based on the principles of Genetics and Darwin’s Principle of Natural Selection. It is frequently used to find optimal or near-optimal solutions to difficult problems which otherwise would take a lifetime to solve. GAs are a subset of a much larger branch of computation known as Evolutionary Computation. GAs were developed by John Holland (1975). 2/1/2021 GENETIC ALGORITHM 4
- 5. GENETIC ALGORITHM: HISTORY Evolutionary computing-1960 by Reichenberg Developed by John Holland , university of Michigan-1970. Got popular in the late 1980’s. Based on ideas from Darwinian Evolution theory “Survival of the fittest”. 1986-Optimization of a Ten Member plane. 2/1/2021 GENETIC ALGORITHM 5
- 6. BIOLOGICAL BACKGROUND Each cell of a living organisms contains chromosomes - strings of DNA. Each chromosome contains a set of genes - blocks of DNA. Each genes encodes a particular pattern - trait. Possible settings of traits - alleles The unique position of the gene in the Chromosome – locus Complete set of genetic material - genome A collection of genes - genotype. A collection of aspects(like eye color)- phenotype. Reproduction involves recombination of genes from parents. The fitness of an organism is how much it can reproduce before it dies. 2/1/2021 GENETIC ALGORITHM 6
- 7. DARWIN'S THEORY OF EVOLUTION All life is related and has descended from a common ancestor. Natural selection – “Survival of the fittest” Organisms can produce more offspring than their surroundings can support -> natural struggle to survive. Organisms whose variations best adapt them to their environments survive, the others die. Variations are heritable -> can be passed on to the next generation -> i.e., evolution 2/1/2021 GENETIC ALGORITHM 7
- 8. EVOLUTION THROUGH NATURAL SELECTION 2/1/2021 GENETIC ALGORITHM 8
- 9. KEY TERMS Individual - Any possible solution. Population - Group of all individuals. Search Space - All possible solutions to the problem. Chromosome - Blueprint for an individual. Trait - Possible aspect(feature) of an individual. Allele - Possible settings of trait(black , blond, etc.,). Locus - The position of a gene on the chromosome. Genome - Collection of all chromosomes for an individual 2/1/2021 GENETIC ALGORITHM 9
- 10. FUNDAMENTALS OF GENETIC ALGORITHM Genetic algorithm mimic the principle of natural genetics and natural selection to construct search and optimization procedure Three most important aspects of using GA are: 1. definition of objective function 2. definition and implementation of genetic representation 3. definition and implementation of genetic operators 2/1/2021 GENETIC ALGORITHM 10
- 11. GA REQUIREMENTS A typical genetic algorithm requires two things to be defined: a genetic representation of the solution domain and a fitness function to evaluate the solution domain. A standard representation of the solution is an array of bits. Arrays of other types and structures can be used in essentially the same way. Tree like representations are explored in genetic programming. 2/1/2021 GENETIC ALGORITHM 11
- 12. BASICS OF GA The most common type of genetic algorithm works like this: a population is created with a group of individuals created randomly. The individuals in the population are then evaluated. The evaluation function is provided by the programmer and gives the individuals a score based on how well they perform at the given task. Two individuals are then selected based on their fitness, the higher the fitness, the higher the chance of being selected. Population of individuals – Individual is feasible solution to problem 2/1/2021 GENETIC ALGORITHM 12
- 13. BASICS OF GA (Cont.) Each individual is characterized by a Fitness function – Higher fitness is better solution Based on their fitness, parents are selected to reproduce offspring for a new generation Fitter individuals have more chance to reproduce New generation has same size as old generation; old generation dies Offspring has combination of properties of two parents If well designed, population will converge to optimal solution 2/1/2021 GENETIC ALGORITHM 13
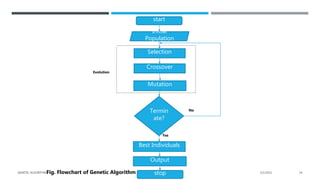
- 14. start Initial Population Selection Crossover Mutation Termin ate? Best Individuals Output stop Yes No Evolution Fig. Flowchart of Genetic Algorithm 2/1/2021 GENETIC ALGORITHM 14
- 15. CREATION OF OFFSPRING During the creation of offspring, recombination occurs (due to cross over) Genes from parents form a whole new chromosome. The new created offspring can be mutated. Mutation means that the element of DNA is modified The fitness of an organism is measured by means of success of organism in life. Search Space The space for all feasible solutions is called search space. Each solution can be marked by its value of the fitness of the problem 2/1/2021 GENETIC ALGORITHM 15
- 16. WORKING PRINCIPLE Consider the optimization problem Maximize f(X) Xi (L) ≤ Xi ≤ Xi (U) for i=1,2,……….., N (1) If we want to minimize f(X), for f(X) >0 , then we can write the objective function as Maximize 𝑥 = 1 1+f(X) (2) If f(X) <0 instead of minimizing f(X), maximize {-f(X)}. Both maximization and minimization problems can be handled by GA 2/1/2021 GENETIC ALGORITHM 16
- 17. SIMPLE GENETIC ALGORITHM 2/1/2021 GENETIC ALGORITHM 17
- 18. NATURE TO COMPUTER MAPPING Nature Computer Population Set of solutions Individual Solution to a problem Fitness Quality of a solution Chromosome Encoding for a Solution Gene Part of the encoding of a solution Reproduction Crossover/Mutation 2/1/2021 GENETIC ALGORITHM 18
- 19. GA OPERATORS AND PARAMETERS 2/1/2021 GENETIC ALGORITHM 19
- 20. ENCODING The process of representing the solution in the form of a string that conveys the necessary information. Just as in a chromosome, each gene controls a particular characteristic of the individual, similarly, each bit in the string represents a characteristic of the solution. 2/1/2021 GENETIC ALGORITHM 20
- 21. ENCODING METHODS Binary Encoding – Most common method of encoding. Chromosomes are strings of 1s and 0s and each position in the chromosome represents a particular characteristic of the problem 2/1/2021 GENETIC ALGORITHM 21
- 22. ENCODING METHODS (Contd.) Octal Encoding - Chromosomes are strings from 0 to 7 To convert any integer to an octal, go on dividing the integer by 8 Hexadecimal Encoding - Chromosomes are represented in hexadecimal numbers Chromosome 1 03467216 Chromosome 2 15723314 Chromosome 1 9CE7 Chromosome 2 3DBA 2/1/2021 GENETIC ALGORITHM 22
- 23. ENCODING METHODS (Contd.) Permutation Encoding – Useful in ordering problems such as the Traveling Salesman Problem (TSP). Example. In TSP , every chromosome is a string of numbers, each of which represents a city to be visited. 2/1/2021 GENETIC ALGORITHM 23
- 24. ENCODING METHODS (Contd.) Value Encoding – Used in problems where complicated values, such as real numbers, are used and where binary encoding would not suffice. Good for some problems, but often necessary to develop some specific crossover and mutation techniques for these chromosomes 2/1/2021 GENETIC ALGORITHM 24
- 25. ENCODING METHODS (Contd.) Tree Encoding– This is mainly used for evolving program expressions for genetic programming. Every chromosome is a tree of some objects such as functions and commands, in a programming language. + x (/5y) Fig. Tree Encoding + / 5 y x 2/1/2021 GENETIC ALGORITHM 25
- 26. FITNESS FUNCTION GA are usually suitable for solving maximization problems. Minimization problems are usually transformed into maximization. A fitness function quantifies the optimality of a solution (chromosome) so that that particular solution may be ranked against all the other solutions. A fitness value is assigned to each solution depending on how close it actually is to solving the problem. Example. In TSP, f(x) is sum of distances between the cities in solution. The lesser the value, the fitter the solution is. 2/1/2021 GENETIC ALGORITHM 26
- 27. FITNESS FUNCTION (Contd.) Fitness function F(X) is first derived from the objective function, Certain genetic operators require that the fitness function be non-negative, certain operators do not have this requirement Consider the transformations, F(X) = f(X) for maximization problem F(X) = 1/f(X) for minimization problem, if f(X) ≠ 0 F(X) = 1/(1+f(X)), if f(X) =0 The fitness function value of the string is known as string’s fitness 2/1/2021 GENETIC ALGORITHM 27
- 28. REPRODUCTION Reproduction is the first operator applied on population Chromosomes are selected from the population to be parents to cross over and produce offspring. The best on should survive and create new offspring. Reproduction operator is sometimes known as the selection operator The various methods for selecting chromosomes for parent to cross over are: 1. Roulette-wheel selection 2. Boltzmann selection 3. Tournament selection 4. Rank selection 5. Steady-state selection 2/1/2021 GENETIC ALGORITHM 28
- 29. ROULETTE –WHEEL SELECTION Main idea: A string is selected from the mating pool with a probability proportional to the fitness Probability of the selected string: Chance to be selected is exactly proportional to fitness Chromosome with bigger fitness will be selected more times 2/1/2021 GENETIC ALGORITHM 29
- 30. ROULETTE –WHEEL SELECTION (Contd.) 1 2 3 4 1 5% 6 8% 7 8% 2 9% 5 20% 3 13% 4 17% 8 20% Fig. Roulette wheel marked for eight individuals according to fitness Area is proportional to the fitness value Fittest individual has largest share of the Roulette- wheel Weakest individual has smallest share of the Roulette- wheel Number of times the Roulette wheel is spun is equal to size of the population Each times the wheel stops, this give the fitter individuals the greatest chance of being selected for the next generation and subsequent mating pool We repeat the extraction as many times as the number of individuals 2/1/2021 GENETIC ALGORITHM 30
- 31. BOLTZMANN SELECTION Simulated annealing is a method of functional minimization or maximization. This method simulates the process of slow cooling of molten metal to achieve the minimum function value in a minimization problem The cooling phenomenon is simulated by controlling a temperature like parameter introduced with the concept of Boltzmann probability distribution so that a system in thermal equilibrium at a temperature T has its energy distributed probabilistically according to P(E) =exp − 𝐸 𝑘𝑇 where k is the Boltzmann constant This expression suggests that a system at a high temperature has almost uniform probability of being at any energy state, but at low temperature it has a low probability of being at a high energy state. By controlling the temperature T and assuming search process follows Boltzmann probability distribution, the convergence of the algorithm is controlled. 2/1/2021 GENETIC ALGORITHM 31
- 32. TOURNAMENT SELECTION A group of n individuals is chosen randomly uniformly from the current population, and the one with the best fitness is selected. n is called the tournament size and can be used to vary the selection pressure. The higher n the higher the pressure to select above average quality individuals. Several tournaments are held between the individuals of current generation. Process is repeated as often as desired (usually until the mating pool is filled). 2/1/2021 GENETIC ALGORITHM 32
- 33. TOURNAMENT SELECTION(Contd.) Tournaments held between pairs are binary tournament selection. Deterministic tournament selection selects the best individual (when p=1) in any tournament. 1-way tournament (k=1) selection is equivalent to random selection. The takeover time for tournament selection is logarithmic to the population size. 2/1/2021 GENETIC ALGORITHM 33
- 34. RANK SELECTION Main idea: First ranks the population and then every chromosome receives fitness from this ranking The worst will have fitness 1, second worst 2 etc. and the best will have fitness N After this all the chromosomes have a chance to be selected. But this method can lead to slower convergence, because the best chromosomes do not differ so much from other ones Disadvantage: the population must be sorted on each cycle 1 2 3 4 5 1 2% 2 5% 3 8% 4 10% 5 75% 2/1/2021 GENETIC ALGORITHM 34
- 35. STEADY-STATE SELECTION Bigger part of chromosome should survive to next generation. In every generation are selected, a few( good individuals with high fitness for maximization problem) chromosome, for creating new offspring. Some (bad with low fitness) chromosomes are removed and new offspring is placed in that place. The rest of population survives to new generation 2/1/2021 GENETIC ALGORITHM 35
- 36. ELITISM Main idea: copy the best chromosomes (solutions) to new population before applying crossover and mutation When creating a new population by crossover or mutation the best chromosome might be lost Forces GAs to retain some number of the best individuals at each generation. Improves performance 2/1/2021 GENETIC ALGORITHM 36
- 37. STOCHASTIC UNIVERSAL SAMPLING A variation of Roulette Wheel Selection. Unlike RWS, to make N selection it only takes a single spin. Selection process proceeds by advancing all the way around the wheel in equal sized steps Distance between pointer = 1/N Where N is the number of pointers 0.95 9 8 7 6 5 4 3 2 10 individua l Pointer 1 Pointer 2 Pointer 3 Pointer 4 Pointer 5 Pointer 6 0.0 0.18 0.34 0.49 0.62 0.73 0.82 1 1.0 Random number 2/1/2021 GENETIC ALGORITHM 37
- 39. RECOMBINATION The primary objective of the recombination operator is to emphasize the good solutions and eliminate the bad solutions in a population, while keeping the population size constant. “Selects The Best, Discards The Rest”. “Recombination” is different from “Reproduction”. Identify the good solutions in a population. Make multiple copies of the good solutions. Eliminate bad solutions from the population so that multiple copies of good solutions can be placed in the population 2/1/2021 GENETIC ALGORITHM 39
- 40. CROSSOVER It is the process in which two chromosomes (strings) combine their genetic material (bits) to produce a new offspring which possesses both their characteristics. Two strings are picked from the mating pool at random to cross over. The method chosen depends on the Encoding Method 2/1/2021 GENETIC ALGORITHM 40
- 41. CROSSOVER METHODS Single Point Crossover- A random point is chosen on the individual chromosomes (strings) and the genetic material is exchanged at this point. 2/1/2021 GENETIC ALGORITHM 41
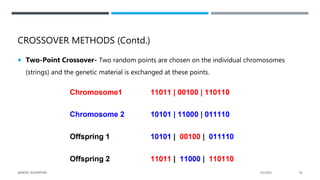
- 42. CROSSOVER METHODS (Contd.) Two-Point Crossover- Two random points are chosen on the individual chromosomes (strings) and the genetic material is exchanged at these points. 2/1/2021 GENETIC ALGORITHM 42
- 43. CROSSOVER METHODS (Contd.) Multipoint Crossover There are two cases in multi-point cross over Even numbered cross-sites: Fig. Multi-point cross over with even number of Cross sites 2/1/2021 GENETIC ALGORITHM 43
- 44. CROSSOVER METHODS (Contd.) Multipoint Crossover (Contd.) Fig. Multi-point cross over with odd number of Cross sites 2/1/2021 GENETIC ALGORITHM 44
- 45. CROSSOVER METHODS (Contd.) Uniform Crossover- Each gene (bit) is selected randomly from one of the corresponding genes of the parent chromosomes. Chromosome 1 1 0 1 1 0 0 1 1 Chromosome 2 0 0 0 1 1 0 1 0 Mask 1 1 0 1 0 1 1 0 Child 1 1 0 0 1 1 0 1 0 Child 2 0 0 1 1 0 0 1 1 2/1/2021 GENETIC ALGORITHM 45
- 46. CROSSOVER METHODS (Contd.) Matrix Cross over - (Two-dimensional cross over) – Each individual is represented as a two-dimensional array of vector. Parent 1 Child 1 Child 2 Before crossing After crossing 2/1/2021 GENETIC ALGORITHM 46
- 47. CROSSOVER (Contd.) Crossover between 2 good solutions MAY NOT ALWAYS yield a better or as good a solution. Since parents are good, probability of the child being good is high. If offspring is not good (poor solution), it will be removed in the next iteration during “Selection”. 2/1/2021 GENETIC ALGORITHM 47
- 48. INVERSION AND DELETION Inversion A string from the population is selected and the bits between two random sites are inverted 0 1 1 1 0 0 1 0 1 0 0 1 1 1 Bits between sites are inverted 2/1/2021 GENETIC ALGORITHM 48
- 49. Deletion and Duplication Any two or three bits at random in order are selected and the previous bits are duplicated. 0 0 1 0 0 1 0 Before Deletion 0 0 1 0 - - 0 At deletion 0 0 1 0 1 0 0 Duplication Deletion and Regeneration Genes between two cross sites are deleted and regenerated randomly 1 0 0 1 1 0 1 1 0 - - - - 1 Deletion 1 0 1 1 0 1 1 Regeneration 2/1/2021 GENETIC ALGORITHM 49
- 50. MUTATION It is the process by which a string is deliberately changed so as to maintain diversity in the population set. Mutation Probability Pm - determines how often the parts of a chromosome will be mutated Example Of Mutation For chromosomes using Binary Encoding, randomly selected bits are inverted 2/1/2021 GENETIC ALGORITHM 50
- 51. GENERATION CYCLE Table shows the generation cycle of the genetic algorithm with a population of four(p1=4) strings with 10 bits each Population P1 String f=Fitness f/f(av) Copy 00000 11100 0.3 0.5 0 100000 11111 0.6 1.0 1 01101 01011 0.6 1.0 1 11111 11011 0.9 1.5 2 Population P2 after reproduction String f=Fitness Cross over CS1 CS2 10000 11111 0.6 4 1 5 01101 01011 0.6 - 11111 11011 0.9 - 11111 11011 0.9 1 1 5 2/1/2021 GENETIC ALGORITHM 51
- 52. GENERATION CYCLE (Contd.) Population P3 after cross over String f=Fitness 11111 11111 1.0 01101 01011 0.6 11111 11011 0.9 10000 11011 0.5 Population P4 after mutation String f=Fitness 01111 11111 0.9 01101 11011 0.7 11111 11011 0.9 10000 11011 0.5 2/1/2021 GENETIC ALGORITHM 52
- 53. CONVERGENCE OF GENETIC ALGORITHM • Convergence is a phenomenon in evolutionary computation that causes evolution to halt because precisely every individual in the population is identical. • Full Convergence might be seen in genetic algorithms using only cross-over. • Premature convergence is when a population has converged to a single solution, but that solution is not as high of quality as expected, i.e. the population has gotten stuck. • However, convergence is not necessarily a negative phenomenon, because populations often stabilize after a time, in the sense that the best programs all have a common ancestor and their behavior is very similar/identical both to each other and to that of high fitness programs from the previous generations. • Convergence can be avoided with a variety of diversity generating techniques. 2/1/2021 GENETIC ALGORITHM 53
- 54. ADVANTAGES OF GAS Does not require any derivative information (which may not be available for many real-world problems). Is faster and more efficient as compared to the traditional methods. Has very good parallel capabilities. Optimizes both continuous and discrete functions and also multi-objective problems Provides a list of “good” solutions and not just a single solution. Always gets an answer to the problem, which gets better over the time. Useful when the search space is very large and there are a large number of parameters involved 2/1/2021 GENETIC ALGORITHM 54
- 55. LIMITATIONS OF GAS Fitness value is calculated repeatedly which might be computationally expensive for some problems. Being stochastic, there are no guarantees on the optimality or the quality of the solution. If not implemented properly, the GA may not converge to the optimal solution 2/1/2021 GENETIC ALGORITHM 55
- 56. REFERENCES 1. Sivananda, Deepa, Principles of Soft Computing, 2ndEdn, Wiley India,2014. 2. Rajasekharan and Viajayalakshmipai, Neural Networks, Fuzzy Logic and Genetic Algorithm, PHI, 2003. (For Unit 5). 2/1/2021 GENETIC ALGORITHM 56