Genetic programming
Download as PPTX, PDF•2 likes•2,060 views
Genetic programming is an evolutionary computation technique that can automatically solve problems without requiring the user to specify the form of the solution in advance. It works by generating an initial population of computer programs randomly, then uses genetic operations like crossover and mutation to breed new programs, evaluating their fitness at each generation. The fittest programs survive and produce offspring for the next generation. Programs in GP are represented as syntax trees with functions as internal nodes and variables/constants as leaves. GP has been successfully applied to problems like circuit design, predictive modeling, and control systems optimization.
Genetic programming
- 2. What is Genetic Programming? • Genetic Programming (GP) is an Evolutionary Computation (EC) technique that automatically solves problems without requiring the user to know or specify the form or structure of the solution in advance, • At the most abstract level, GP is a systematic, domain-independent method for getting computers to solve problems automatically starting from a high-level statement of what needs to be done
- 3. Why Genetic Programming • It saves time by freeing the human from having to design complex algorithms, • Not only designing the algorithms but creating ones that give optimal solutions
- 4. How Genetic Programming? The basic control flow for genetic programming, where survival of the fittest is used to find solutions, is shown below:
- 5. The basic steps in a GP system Algorithm
- 6. The basic steps in a GP system • GP finds out how well a program works by running it, and then comparing its behavior to some ideal (line 3), • We might be interested, for example, in how well a program predicts a time series or controls an industrial process, • This comparison is quantified to give a numeric value called fitness, • Those programs that do well are chosen to breed (line 4) and produce new programs for the next generation (line 5)
- 7. The basic steps in a GP system • The primary genetic operations that are used to create new programs from existing ones are: Crossover: The creation of a child program by combining randomly chosen parts from two selected parent programs, Mutation: The creation of a new child program by randomly altering a randomly chosen part of a selected parent program
- 9. Representation of Solutions in a GP System The tree representation of the program: max(x+x,x+3*y)
- 10. In more advanced forms of GP
- 14. Representation of Solutions in a GP System • In GP, programs are usually expressed as syntax trees rather than as lines of code, • The variables and constants in the program (x, y and 3) are leaves of the tree and in GP they are called terminals, whilst the arithmetic operations (+, * and max) are internal nodes called functions, • The sets of allowed functions and terminals together form the primitive set of a GP System • In more advanced forms of GP, programs can be composed of multiple components (e.g., subroutines), • In this case, the representation used in GP is a set of trees grouped together under a special root node that acts as glue. • The (sub)trees are called branches and the number and type of the branches in a program, together with certain other features of their structure, form the architecture of the program. • It is common in the GP literature to represent expressions in a prefix notation, • For example, max(x+x,x+3*y) becomes (max (+ x x) (+ x (* 3 y))), • This notation often makes it easier to see the relationship between (sub)expressions and their corresponding (sub)trees, • The trees and their corresponding prefixnotation expressions are used interchangeably
- 16. Initializing the Population • In GP, the individuals in the initial population are typically randomly generated, • There are a number of different approaches for generating this random initial population, • Next, two of the simplest (and earliest) methods (the full and grow methods), and a widely used combination of the two known as Ramped half-and-half
- 17. The Full Method • The next slide shows a series of snapshots of the construction of a full tree of depth 2, • The children of the * and / nodes must be leaves or otherwise the tree would be too deep, • Thus, at both steps t = 3, t = 4, t = 6 and t = 7 a terminal must be chosen (x, y, 1 and 0, respectively). • Creation of a full tree having maximum depth 2 using the full initialization method (t = time)
- 18. The Full Method Initialization Example
- 19. The Full Method Initialization Example
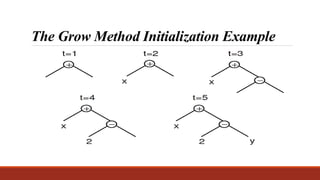
- 20. Initializing the Population: Grow Method • The grow method, on the contrary, allows for the creation of trees of more varied sizes and shapes, • Nodes are selected from the whole primitive set (i.e., functions and terminals) until the depth limit is reached, • Once the depth limit is reached only terminals may be chosen (just as in the full method), • The next slide illustrates this process for the construction of a tree with depth limit 2 • Creation of a five node tree using the grow initialisation method with a maximum depth of 2 (t = time) • A terminal is chosen at t = 2, causing the left branch of the root to be closed at that point even though the maximum depth had not been reached
- 21. The Grow Method Initialization Example
- 23. Initializing the Population: half-and-half Method Because neither the grow or full method provide a very wide array of sizes or shapes on their own, a combination called ramped half-and- half proposed, • Half the initial population is constructed using full and half is constructed using grow, • This is done using a range of depth limits (hence the term “ramped”) to help ensure that we generate trees having a variety of sizes and shapes
- 24. Recombination and Crossover • The most commonly used form of crossover is subtree crossover, • Given two parents, subtree crossover randomly selects a crossover point (a node) in each parent tree, • It creates the offspring by replacing the subtree rooted at the crossover point in a copy of the first parent with a copy of the subtree rooted at the crossover point in the second parent, for example
- 26. Recombination and Mutation • The most commonly used form of mutation in GP (called subtree mutation) randomly selects a mutation point in a tree and substitutes the subtree rooted there with a randomly generated subtree, • This is illustrated by the example of the next slide
- 29. Applying GP System to a Problem
- 30. Examples of primitives in GP function and terminal sets
- 31. The development of the topology and the sizing of an electrical circuit
- 32. Function development for appraising brittleness of intact rocks using genetic programming and non-linear multiple regression models
- 33. Proposed model Training Testing R 2 RMSE VAF R 2 RMSE VAF NLMR 0.817 4.382 80.231 0.882 3.602 86.701 GP 0.909 2.862 90.648 0.904 3.509 88.943 R2 :Coefficient of determination RMSE: Root Mean Square Error VRF: Variance account for
- 35. GP is much more power full than GA. The output of the GA is a quantity, while output of GP is a another computer program. Where there is no ideal solution, GP works best (ex. A program that drives a car).