Graph Coloring : Greedy Algorithm & Welsh Powell Algorithm

Maulana Azad NationalMaulana Azad National InstituteInstitute ofof
TechnologyTechnology
Department of Computer Science & EngineeringDepartment of Computer Science & Engineering
PresentationPresentation
OnOn
Graph ColoringGraph Coloring
Presented By:Presented By:
Priyank JainPriyank Jain
Shweta SaxenaShweta Saxena

What is Graph Coloring?What is Graph Coloring?
 Graph Coloring is an assignment of colorsGraph Coloring is an assignment of colors
(or any distinct marks) to the vertices of a(or any distinct marks) to the vertices of a
graph. Strictly speaking, a coloring is agraph. Strictly speaking, a coloring is a
proper coloring if no two adjacent verticesproper coloring if no two adjacent vertices
have the same color.have the same color.

Origin of the problemOrigin of the problem

Why Graph Coloring?Why Graph Coloring?
 Many problems can be formulated as aMany problems can be formulated as a
graph coloring problem including Timegraph coloring problem including Time
Tabling,Tabling, Channel AssignmentChannel Assignment etc.etc.
 A lot of research has been done in thisA lot of research has been done in this
area.area.

Channel AssignmentChannel Assignment
 Find a channel assignment to R radioFind a channel assignment to R radio
stations such that no station has a conflictstations such that no station has a conflict
(there is a conflict if they are in vicinity)(there is a conflict if they are in vicinity)
 Vertices – radio stations, edges – conflict,Vertices – radio stations, edges – conflict,
colors – available channelscolors – available channels

TerminologyTerminology
 K-ColoringK-Coloring
 A k-coloring of a graph G is a mapping ofA k-coloring of a graph G is a mapping of
V(G) onto the integers 1..k such that adjacentV(G) onto the integers 1..k such that adjacent
vertices map into different integers.vertices map into different integers.
 A k-coloring partitions V(G) into k disjointA k-coloring partitions V(G) into k disjoint
subsets such that vertices from differentsubsets such that vertices from different
subsets have different colors.subsets have different colors.

 K-colorableK-colorable
 A graph G is k-colorable if it has a k-coloring.A graph G is k-colorable if it has a k-coloring.
 Chromatic NumberChromatic Number
 The smallest integer k for which G is k-The smallest integer k for which G is k-
colorable is called the chromatic number of G.colorable is called the chromatic number of G.

 K-chromatic graphK-chromatic graph
 A graph whose chromatic number is k isA graph whose chromatic number is k is
called a k-chromatic graph.called a k-chromatic graph.
 ColoringColoring
 A coloring of a graph G assigns colors to theA coloring of a graph G assigns colors to the
vertices of G so that adjacent vertices arevertices of G so that adjacent vertices are
given different colorsgiven different colors

Types of Graph ColoringTypes of Graph Coloring
 Vertex ColoringVertex Coloring
 Edge ColoringEdge Coloring

ExampleExample
The chromatic number is four. Therefore this a 4-Chromatic Graph

ExampleExample
 Problem: A state legislature has aProblem: A state legislature has a
number of committees that meet eachnumber of committees that meet each
week for one hour. How can we scheduleweek for one hour. How can we schedule
the committee meetings times such thatthe committee meetings times such that
the least amount of time is used but suchthe least amount of time is used but such
that two committees with overlappingthat two committees with overlapping
membership do not meet at the samemembership do not meet at the same
time.time.

Example (cont)Example (cont)
The chromatic number of this graph is four. Thus four hours suffice to schedule
committee meetings without conflict.
An edge represents a conflict between to meetings
An vertex represents a meeting

Graph Colouring AlgorithmGraph Colouring Algorithm
 There is no efficient algorithm available forThere is no efficient algorithm available for
coloring a graph with minimum number ofcoloring a graph with minimum number of
colors.colors.
 Graph coloring problem is a known NPGraph coloring problem is a known NP
Complete problem.Complete problem.

NP Complete ProblemNP Complete Problem
 NP complete problems are problemsNP complete problems are problems
whose status is unknown.whose status is unknown.
 No polynomial time algorithm has yetNo polynomial time algorithm has yet
been discovered for any NP completebeen discovered for any NP complete
problemproblem
 It is not established that no polynomial-It is not established that no polynomial-
time algorithm exist for any of them.time algorithm exist for any of them.

NP Complete ProblemNP Complete Problem
 The interesting part is, if any one of theThe interesting part is, if any one of the
NP complete problems can be solved inNP complete problems can be solved in
polynomial time, then all of them can bepolynomial time, then all of them can be
solved.solved.
 Although Graph coloring problem is NPAlthough Graph coloring problem is NP
Complete problem there are someComplete problem there are some
approximate algorithms to solve the graphapproximate algorithms to solve the graph
coloring problem.coloring problem.

Basic Greedy AlgorithmBasic Greedy Algorithm
1.1. Color first vertex with first color.Color first vertex with first color.
2. Do following for remaining V-1 vertices.2. Do following for remaining V-1 vertices.
a)a) Consider the currently picked vertexConsider the currently picked vertex
and color it with the lowest numberedand color it with the lowest numbered
color that has not been used on anycolor that has not been used on any
previously colored vertices adjacent to it.previously colored vertices adjacent to it.
If all previously used colors appear onIf all previously used colors appear on
vertices adjacent to v, assign a new colorvertices adjacent to v, assign a new color
to it.to it.

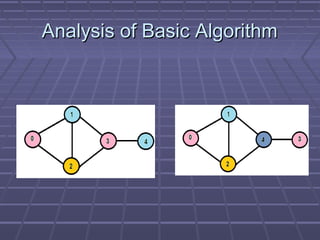
Analysis of Greedy AlgorithmAnalysis of Greedy Algorithm
The above algorithm doesn’t always useThe above algorithm doesn’t always use
minimum number of colors. Also, theminimum number of colors. Also, the
number of colors used sometime dependnumber of colors used sometime depend
on the order in which vertices areon the order in which vertices are
processedprocessed

Example:Example:
 For example, consider the following twoFor example, consider the following two
graphs. Note that in graph on right side,graphs. Note that in graph on right side,
vertices 3 and 4 are swapped. If wevertices 3 and 4 are swapped. If we
consider the vertices 0, 1, 2, 3, 4 in leftconsider the vertices 0, 1, 2, 3, 4 in left
graph, we can color the graph using 3graph, we can color the graph using 3
colors. But if we consider the vertices 0, 1,colors. But if we consider the vertices 0, 1,
2, 3, 4 in right graph, we need 4 colors2, 3, 4 in right graph, we need 4 colors

Analysis of Basic AlgorithmAnalysis of Basic Algorithm

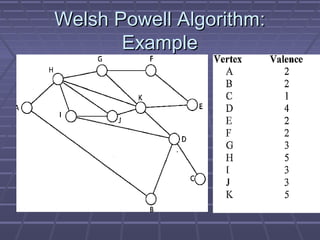
WelshWelsh PowellPowell AlgorithmAlgorithm
 Find the degree of each vertexFind the degree of each vertex
 ListList the vericesthe verices in order of descendingin order of descending
valence i.e.valence i.e. degree(v(i))>=degree(v(i+1))degree(v(i))>=degree(v(i+1))
 ColourColour the first vertex in the listthe first vertex in the list
 Go down the sorted list and color everyGo down the sorted list and color every
vertex not connected to the coloredvertex not connected to the colored
vertices above the same color then crossvertices above the same color then cross
out all colored vertices in the list.out all colored vertices in the list.

Welsh Powell AlgorithmWelsh Powell Algorithm
 Repeat the process on the uncoloredRepeat the process on the uncolored
vertices with a new color-always workingvertices with a new color-always working
in descending order of degree until allin descending order of degree until all
vertices are colored.vertices are colored.
 ComplexityComplexity of above algorithm =of above algorithm = O(nO(n22
))

Welsh Powell Algorithm:Welsh Powell Algorithm:
ExampleExample

Graph Coloring : Greedy Algorithm & Welsh Powell Algorithm

More Related Content

What's hot (20)

Similar to Graph Coloring : Greedy Algorithm & Welsh Powell Algorithm (20)

Recently uploaded (20)

Graph Coloring : Greedy Algorithm & Welsh Powell Algorithm

Editor's Notes