![● Spatial-based methods define graph convolutions based on a node’s spatial relations. Images can be considered as a
special form of graph with each pixel representing a node.
● [1] Neural Network for Graphs (NN4G)
○ learns graph mutual dependency through a compositional neural
architecture with independent parameters at each layer.
● [2] Diffusion Convolutional Neural Network (DCNN)
○ regards graph convolutions as a diffusion
process. It assumes information is
transferred from one node to one of its
neighboring nodes with a certain transition
Probability.
○ the hidden representation matrix H(k)
remains the same dimension as the input
feature matrix X and is not a function of its
previous hidden representation matrix
H(k−1)
○ DCNN concatenates H(1) , H(2) , · · · , H(K)
together as the final model outputs.
○ DCNNs are learned via stochastic minibatch
gradient descent on backpropagated error
https://arxiv.org/pdf/1511.02136.pdf
Graph level Read out function
with learnable parameters](https://image.slidesharecdn.com/graphneuralnetworks-overview-210313205158/85/Graph-neural-networks-overview-23-320.jpg)
Graph neural networks overview
- 1. Graph Neural Networks overview summary from https://arxiv.org/pdf/1901.00596.pdf (Zonghan Wu et al. 2019-12) and other papers.. R. Kiriukhin
- 2. Existing overviews: 1. M. M. Bronstein, J. Bruna, Y. LeCun, A. Szlam, and P. Vandergheynst, “Geometric deep learning: going beyond euclidean data,” IEEE Signal Processing Magazine, vol. 34, no. 4, pp. 18–42, 2017. ○ deep learning methods in the non-Euclidean domain, including graphs and manifolds 2. W. L. Hamilton, R. Ying, and J. Leskovec, “Representation learning on graphs: Methods and applications,” in Proc. of NIPS, 2017, pp. 1024–1034. ○ network embedding 3. P. W. Battaglia, J. B. Hamrick, V. Bapst, A. Sanchez-Gonzalez, V. Zambaldi, M. Malinowski, A. Tacchetti, D. Raposo, A. Santoro, R. Faulkner et al., “Relational inductive biases, deep learning, and graph networks,” arXiv preprint arXiv:1806.01261, 2018. ○ learning from relational data 4. J. B. Lee, R. A. Rossi, S. Kim, N. K. Ahmed, and E. Koh, “Attention models in graphs: A survey,” arXiv preprint arXiv:1807.07984, 2018. ○ GNNs which apply different attention mechanisms
- 3. Motivation: features of “graph data” ● Handcrafted features ● Automatically created features (DL): ○ RNN(1980), CNN(1988) - exploit spatial structure of the sample ○ Autoencoder Graph Network is a generalisation where structure of the data is irregular: ● variable size ● unordered nodes ● number of neighbors differs for different nodes ● relationships no longer only spatial (“near”) but all kinds of interactions: “bought”, “cited”, “accessed”... makes “convolutions” problematic
- 6. Graph neural networks vs. network embedding ● Network embedding aims at representing network nodes as low-dimensional vector representations, preserving both network topology structure and node content information, so that any subsequent graph analytics task such as classification, clustering, and recommendation can be easily performed using simple off-the-shelf machine learning algorithms (e.g., support vector machines for classification). ○ contains other non-deep learning methods such as matrix factorization and random walks ○ Z Yang, CMU EDU, WW Cohen, R Salakhutdinov Revisiting Semi-Supervised Learning with Graph Embeddings, (github) ○ WL-1 algorithm (Weisfeiler & Lehmann, 1968) (rus, eng, eng2, wl-based graph kernels ) ● GNNs are deep learning models aiming at addressing graph-related tasks in an end-to-end manner. Many GNNs explicitly extract high-level representations. ○ can address the network embedding problem through a graph autoencoder framework.
- 7. Graph neural networks vs. graph kernel methods ● Graph kernels are historically dominant techniques to solve the problem of graph classification. These methods employ a kernel function to measure the similarity between pairs of graphs so that kernel-based algorithms like support vector machines can be used for supervised learning on graphs. ○ “Deep graph kernels decompose a graph into substructures, treat those substructures as words in a sentence, and fit a word-embedding model to obtain a vectorization” ○ similar to GNNs, graph kernels can embed graphs or nodes into vector spaces by a mapping function ○ the difference is that this mapping function is deterministic rather than learnable ○ due to a pair-wise similarity calculation, graph kernel methods suffer significantly from computational bottlenecks ● GNNs ○ directly perform graph classification based on the extracted graph representations and therefore are much more efficient than graph kernel methods
- 9. ● Recurrent graph neural networks (RecGNNs) ○ pioneer works of graph neural networks. RecGNNs aim to learn node representations with recurrent neural architectures ● Convolutional graph neural networks (ConvGNNs) ○ generalize the operation of convolution from grid data to graph data. ● Graph autoencoders (GAEs) ○ unsupervised learning frameworks which encode nodes/graphs into a latent vector space and reconstruct graph data from the encoded information ● Spatial-temporal graph neural networks (STGNNs) ○ aim to learn hidden patterns from spatial-temporal graphs
- 10. Frameworks: ● Entity level (<entity> classification, <entity> embedding …): ○ Node ○ Graph ○ Edge ● Learning: Semi-supervised learning for node-level classification ○ Given a single network with partial nodes being labeled and others remaining unlabeled, ConvGNNs can learn a robust model that effectively identifies the class labels for the unlabeled nodes ● Learning: Supervised learning for graph-level classification ○ Graph-level classification aims to predict the class label(s) for an entire graph ● Learning: Unsupervised learning for graph embedding ○ When no class labels are available in graphs, we can learn the graph embedding in a purely unsupervised way in an end to end framework. ■ embed the graph into the latent representation upon which a decoder is used to reconstruct the graph structure ■ utilize the negative sampling approach which samples a portion of node pairs as negative pairs while existing node pairs with links in the graphs are positive pairs. Then a logistic regression layer is applied to distinguish between positive and negative pairs
- 11. Recurrent raph neural networks: RecGNNs -
- 12. RecGNN 1997+ History: 1. A. Sperduti and A. Starita, “Supervised neural networks for the classification of structures,” IEEE Transactions on Neural Networks, vol. 8, no. 3, pp. 714–735, 1997. ○ applied neural networks to directed acyclic graphs 2. M. Gori, G. Monfardini, and F. Scarselli, “A new model for learning in graph domains,” in Proc. of IJCNN, vol. 2. IEEE, 2005, pp. 729–734. ○ initially outlined the notion of graph neural networks 3. F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner, and G. Monfardini, “The graph neural network model,” IEEE Transactions on Neural Networks, vol. 20, no. 1, pp. 61–80, 2009. 4. C. Gallicchio and A. Micheli, “Graph echo state networks,” in IJCNN. IEEE, 2010, pp. 1–8. ○ further elaborated
- 13. ● They assume a node in a graph constantly exchanges information/message with its neighbors until a stable equilibrium is reached. Target node’s representation learned by propagating neighbor information in an iterative manner until a stable fixed point is reached ● “vanilla” RecGNN ○ f() must be special, contracting, to ensure convergence ■ could be NN (with penalized J(W)) ■ could be GRU (GGRN) ○ update could be asynchronous (SSE) ○ when a convergence criterion is satisfied, the last step node hidden states are forwarded to a readout layer. ○ GNN alternates the stage of node state propagation and the stage of parameter gradient computation to minimize a training objective ● Convolutional graph neural networks (ConvGNNs) are closely related to recurrent graph neural networks. Instead of iterating node states with contractive constraints, ConvGNNs address the cyclic mutual dependencies architecturally using a fixed number of layers with different weights in each layer.
- 14. Convolutional graph neural networks: ConvGNNs -
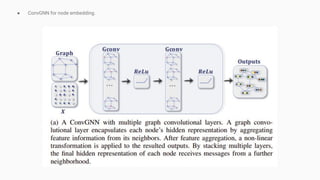
- 15. ● ConvGNN for node embedding.
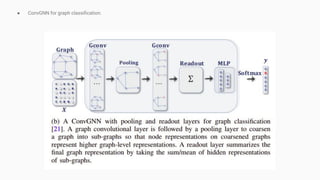
- 16. ● ConvGNN for graph classification.
- 17. ConvGNN: spectral-based (convolutional graph neural networks). 2014+ History: 1. J. Bruna, W. Zaremba, A. Szlam, and Y. LeCun, “Spectral networks and locally connected networks on graphs,” in Proc. of ICLR, 2014. ○ The first prominent research on spectral-based ConvGNNs (spatial approach is also there btw) 2. M. Henaff, J. Bruna, and Y. LeCun, “Deep convolutional networks on graph-structured data,” arXiv preprint arXiv:1506.05163, 2015. 3. M. Defferrard, X. Bresson, and P. Vandergheynst, “Convolutional neural networks on graphs with fast localized spectral filtering,” in Proc. of NIPS, 2016, pp. 3844–3852. (github) 4. T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” in Proc. of ICLR, 2017. 5. R. Levie, F. Monti, X. Bresson, and M. M. Bronstein, “Cayleynets: Graph convolutional neural networks with complex rational spectral filters,” IEEE Transactions on Signal Processing, vol. 67, no. 1, pp. 97–109, 2017. ○ improvements, extensions, and approximations on spectral-based ConvGNNs
- 18. ● Spectral based approaches define graph convolutions by introducing filters from the perspective of graph signal processing where the graph convolutional operation is interpreted as removing noises from graph signals. ● They assume graphs to be undirected. * normalized symmetric graph Laplacian matrix (Adjacency, Degree) * eigen decomposition of L * node->R (from graph signal processing) * graph Fourier transform. * graph inverse Fourier transform * graph convolution of signal x with filter g OR if
- 19. ● The global structure of the graph can be exploited with the spectrum of its graph-Laplacian to generalize the convolution operator.
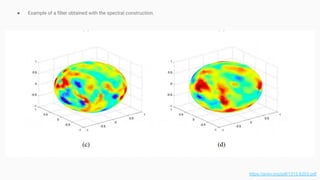
- 21. ● Example of a filter obtained with the spectral construction. https://arxiv.org/pdf/1312.6203.pdf
- 22. ConvGNN: spatial-based (convolutional graph neural networks). 2009+ History: 1. ($) A. Micheli, “Neural network for graphs: A contextual constructive approach,” IEEE Transactions on Neural Networks, vol. 20, no. 3, pp. 498–511, 2009. ○ first addressed graph mutual dependency by architecturally composite nonrecursive layers while inheriting ideas of message passing from RecGNNs 2. J. Atwood and D. Towsley, “Diffusion-convolutional neural networks,” in Proc. of NIPS, 2016, pp. 1993–2001. 3. M. Niepert, M. Ahmed, and K. Kutzkov, “Learning convolutional neural networks for graphs,” in Proc. of ICML, 2016, pp. 2014–2023. 4. J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, and G. E. Dahl, “Neural message passing for quantum chemistry,” in Proc. of ICML, 2017, pp. 1263–1272.
- 23. ● Spatial-based methods define graph convolutions based on a node’s spatial relations. Images can be considered as a special form of graph with each pixel representing a node. ● [1] Neural Network for Graphs (NN4G) ○ learns graph mutual dependency through a compositional neural architecture with independent parameters at each layer. ● [2] Diffusion Convolutional Neural Network (DCNN) ○ regards graph convolutions as a diffusion process. It assumes information is transferred from one node to one of its neighboring nodes with a certain transition Probability. ○ the hidden representation matrix H(k) remains the same dimension as the input feature matrix X and is not a function of its previous hidden representation matrix H(k−1) ○ DCNN concatenates H(1) , H(2) , · · · , H(K) together as the final model outputs. ○ DCNNs are learned via stochastic minibatch gradient descent on backpropagated error https://arxiv.org/pdf/1511.02136.pdf Graph level Read out function with learnable parameters
- 24. ● Diffusion Graph Convolution (DGC) ○ sums up outputs at each diffusion step instead of concatenation ○ using the power of a transition probability matrix implies that distant neighbors contribute very little information to a central node Other variations: ● Taking short path between nodes v and u: stacking convolved features from nodes with j hops from the current one ● By grouping adjacent nodes into Q groups according to particular criteria (not necessarily shortest path) and applying separate W for separate groups (defined by Âdjacency). (PGC) ● By allowing a “message passing” to happen K times (MPNN). ● GIN, GraphSage (weighted) ● GAT, GAAN, (attention)
- 25. ● Pooling ○ graph coarsening ○ mean/max/sum pooling ○ LSTM before pooling to save order information in memory ○ node rearrangement ● Shape of receptive field ○ ConvGNN is able to extract global information by stacking local graph convolutional layers Other ConvGNN aspects ● VC dimension ○ O(p4 n2 ) for tanh/sigmoid activation ● Graph isomorphism ○ If graphs G1 and G2 non-isomorphic -> if a GNN maps G1 and G2 to different embeddings, these two graphs can be identified as non-isomorphic by the Weisfeiler-Lehman (WL) test. If the aggregation functions and the readout functions of a GNN are injective, the GNN is at most as powerful as the WL test in distinguishing different graphs. ● Equivariance and invariance ○ must be an equivariant function when performing node-level tasks and must be an invariant function when performing graph-level tasks ● Universal approximation ○ <complicated>
- 27. GAE: . 2016+ History: 1. S. Cao, W. Lu, and Q. Xu, “Deep neural networks for learning graph representations,” in Proc. of AAAI, 2016, pp. 1145–1152.. 2. D. Wang, P. Cui, and W. Zhu, “Structural deep network embedding,” in Proc. of KDD. ACM, 2016, pp. 1225–1234. 3. T. N. Kipf and M. Welling, “Variational graph auto-encoders,” NIPS Workshop on Bayesian Deep Learning, 2016. 4. S. Pan, R. Hu, G. Long, J. Jiang, L. Yao, and C. Zhang, “Adversarially regularized graph autoencoder for graph embedding.” in Proc. of IJCAI, 2018, pp. 2609–2615. 5. K. Tu, P. Cui, X. Wang, P. S. Yu, and W. Zhu, “Deep recursive network embedding with regular equivalence,” in Proc. of KDD. ACM, 2018, pp. 2357–2366. 6. W. Yu, C. Zheng, W. Cheng, C. C. Aggarwal, D. Song, B. Zong, H. Chen, and W. Wang, “Learning deep network representations with adversarially regularized autoencoders,” in Proc. of AAAI. ACM, 2018, pp. 2663–2671. 7. Y. Li, O. Vinyals, C. Dyer, R. Pascanu, and P. Battaglia, “Learning deep generative models of graphs,” in Proc. of ICML, 2018.
- 28. ● T. N. Kipf and M. Welling, “Variational graph auto-encoders,”
- 29. ● -
- 30. Spatial-temporal graph neural networks: STGNNs -
- 31. STGNN: . 2018+ History: 1. J. Zhang, X. Shi, J. Xie, H. Ma, I. King, and D.-Y. Yeung, “Gaan: Gated attention networks for learning on large and spatiotemporal graphs,” in Proc. of UAI, 2018. 2. Y. Seo, M. Defferrard, P. Vandergheynst, and X. Bresson, “Structured sequence modeling with graph convolutional recurrent networks,” in International Conference on Neural Information Processing. Springer, 2018, pp. 362–373. 3. Y. Li, R. Yu, C. Shahabi, and Y. Liu, “Diffusion convolutional recurrent neural network: Data-driven traffic forecasting,” in Proc. of ICLR, 2018. 4. A. Jain, A. R. Zamir, S. Savarese, and A. Saxena, “Structural-rnn: Deep learning on spatio-temporal graphs,” in Proc. of CVPR, 2016, pp. 5308–5317. 5. B. Yu, H. Yin, and Z. Zhu, “Spatio-temporal graph convolutional networks: A deep learning framework for traffic forecasting,” in Proc. of IJCAI, 2018, pp. 3634–3640. 6. S. Yan, Y. Xiong, and D. Lin, “Spatial temporal graph convolutional networks for skeleton-based action
- 33. Code? -
- 35. M. Wang, L. Yu, D. Zheng, Q. Gan, Y. Gai, Z. Ye, M. Li, J. Zhou, Q. Huang, C. Ma, Z. Huang, Q. Guo, H. Zhang, H. Lin, J. Zhao, J. Li, A. J. Smola, and Z. Zhang, “Deep graph library: Towards efficient and scalable deep learning on graphs,”
- 36. Thank you!