Greedy algorithm

Sunawar Khan
Islamia University of Bahawalpur
Bahawalnagar Campus
Analysis o f Algorithm

‫خان‬ ‫سنور‬ Algorithm Analysis
Areas of Greedy
Introduction to Greedy Algorithm
Contents
Components of Greedy Technique
0-1 Knapsack Problem

Optimization Problems
• A problem that may have many feasible solutions.
• Each solution has a value
• In maximization problem, we wish to find a solution to maximize the
value
• In the minimization problem, we wish to find a solution to minimize
the value

Technique to Solve a Problem
• Greedy Method
• Dynamic Programming
• Branch and Bound

Greedy Algorithms
• Many optimization problems can be solved using a greedy approach
• The basic principle is that local optimal decisions may be used to build an
optimal solution
• But the greedy approach may not always lead to an optimal solution overall
for all problems
• The key is knowing which problems will work with this approach and which
will not
• We will study
• The Knapsack Problem

Greedy algorithms
• A greedy algorithm always makes the choice that looks best at the
moment
• My everyday examples:
• Driving in Los Angeles, NY, or Boston for that matter
• Playing cards
• Invest on stocks
• Choose a university
• The hope: a locally optimal choice will lead to a globally optimal solution
• For some problems, it works
• Greedy algorithms tend to be easier to code

Greedy Technique
• Greedy algorithms are simple and straightforward.
• They are shortsighted in their approach in the sense that they take
decisions on the basis of information at hand without worrying about
the effect these decisions may have in the future.
• They are easy to invent, easy to implement and most of the time
quite efficient.
• Many problems cannot be solved correctly by greedy approach.
Greedy algorithms are used to solve optimization problems

Greedy Approach
• Greedy Algorithm works by making the decision that seems most
promising at any moment; it never reconsiders this decision, whatever
situation may arise later.

Algorithm
Algorithm Greedy(a, n){
for i=1 to n do
X = Select(a);
If feasible(x) then
Solution = Solution + x;
}

A simple example
• Problem: Pick k numbers out of n numbers such that the sum of these
k numbers is the largest.
• Algorithm:
FOR i = 1 to k
pick out the largest number and
delete this number from the input.
ENDFOR

The greedy method
• Suppose that a problem can be solved by a sequence of decisions.
The greedy method has that each decision is locally optimal. These
locally optimal solutions will finally add up to a globally optimal
solution.
• Only a few optimization problems can be solved by the greedy
method.

Another Example
• As an example consider the problem of "Making Change".
• Coins available are:
• dollars (100 cents)
• quarters (25 cents)
• dimes (10 cents)
• nickels (5 cents)
• pennies (1 cent)

Making Change Problem
• Problem Make a change of a given amount using the smallest
possible number of coins.
• Informal Algorithm
• Start with nothing.
• at every stage without passing the given amount.
• add the largest to the coins already chosen.

Formal Algorithm
• Make change for n units using the least possible number of
coins.
• MAKE-CHANGE (n)
C ← {100, 25, 10, 5, 1}// constant.
Sol ← {}; // set that will hold the solution set.
Sum ← 0 sum of item in solution set
WHILE sum not = n
x = largest item in set C such that sum + x ≤
n
IF no such item THEN
RETURN "No Solution"
S ← S {value of x}
sum ← sum + x
RETURN S

Features of Problems solved by Greedy Algorithms
• To construct the solution in an optimal way. Algorithm maintains two
sets. One contains chosen items and the other contains rejected
items.
• The greedy algorithm consists of four (4) function.
• A Candidate Set:- Solution is created from this set.
• A Selection Set:- A Function used to chose the best candidate to be added to
the solution.
• A Feasibility Set:- A function that checks the feasibility of a set.
• A Objective Function:- A Function which is used to assign value to a solution
or partial solution.
• A Solution Function:- A Function which is used to indicate whether a complete
solution has been reached

Structure of Greedy Algorithm
• Initially the set of chosen items is empty i.e., solution set.
• At each step
• item will be added in a solution set by using selection function.
• IF the set would no longer be feasible
• reject items under consideration (and is never consider again).
• ELSE IF set is still feasible THEN
• add the current item.

Definition of Feasibility
• A feasible set (of candidates) is promising if it can be extended to produce
not merely a solution, but an optimal solution to the problem. In particular,
the empty set is always promising why? (because an optimal solution always
exists)
• Unlike Dynamic Programming, which solves the subproblems bottom-up, a
greedy strategy usually progresses in a top-down fashion, making one
greedy choice after another, reducing each problem to a smaller one.
• Greedy-Choice Property
• The "greedy-choice property" and "optimal substructure" are two ingredients in the
problem that lend to a greedy strategy.
• Greedy-Choice Property
• It says that a globally optimal solution can be arrived at by making a locally optimal
choice.

Shortest paths on a special graph
• Problem: Find a shortest path from v0 to v3.
• The greedy method can solve this problem.
• The shortest path: 1 + 2 + 4 = 7.

Shortest paths on a multi-stage graph
• Problem: Find a shortest path from v0 to v3 in the multi-stage graph.
• Greedy method: v0v1,2v2,1v3 = 23
• Optimal: v0v1,1v2,2v3 = 7
• The greedy method does not work.

Minimum spanning trees (MST)
• It may be defined on Euclidean space points or on a graph.
• G = (V, E): weighted connected undirected graph
• Spanning tree : S = (V, T), T  E, undirected tree
• Minimum spanning tree(MST) : a spanning tree with the smallest total
weight.

An example of MST
• A graph and one of its minimum costs spanning tree

Kruskal’s algorithm for finding MST
Step 1: Sort all edges into nondecreasing order.
Step 2: Add the next smallest weight edge to the forest if it will not
cause a cycle.
Step 3: Stop if n-1 edges. Otherwise, go to Step2.

An example of Kruskal’s algorithm

Prim’s algorithm for finding MST
Step 1: x  V, Let A = {x}, B = V - {x}.
Step 2: Select (u, v)  E, u  A, v  B such that (u, v) has the smallest
weight between A and B.
Step 3: Put (u, v) in the tree. A = A  {v}, B = B - {v}
Step 4: If B = , stop; otherwise, go to Step 2.
• Time complexity : O(n2), n = |V|.
(see the example on the next page)

An example for Prim’s algorithm

The single-source shortest path problem
• shortest paths from v0 to all destinations

Dijkstra’s algorithm
1 2 3 4 5 6 7 8
1 0
2 300 0
3 1000 800 0
4 1200 0
5 1500 0 250
6 1000 0 900 1400
7 0 1000
8 1700 0
In the cost adjacency matrix, all entries
not shown are +.

• Time complexity : O(n2), n = |V|.
Vertex
Iteration S Selected (1) (2) (3) (4) (5) (6) (7) (8)
Initial ----
1 5 6 + + + 1500 0 250 + +
2 5,6 7 + + + 1250 0 250 1150 1650
3 5,6,7 4 + + + 1250 0 250 1150 1650
4 5,6,7,4 8 + + 2450 1250 0 250 1150 1650
5 5,6,7,4,8 3 3350 + 2450 1250 0 250 1150 1650
6 5,6,7,4,8,3 2 3350 3250 2450 1250 0 250 1150 1650
5,6,7,4,8,3,2 3350 3250 2450 1250 0 250 1150 1650
Dijkstra’s algorithm

Knapsack Problem
• Statement A thief robbing a store and can carry a maximal
weight of w into their knapsack. There are n items
and ith item weigh wi and is worth vi dollars. What items
should thief take?
• There are two versions of problem

Fractional knapsack problem
• The setup is same, but the thief can take fractions of items,
meaning that the items can be broken into smaller pieces so
that thief may decide to carry only a fraction of xi of item i,
where 0 ≤ xi ≤ 1.Exhibit greedy choice property.
• Greedy algorithm exists.
• Exhibit optimal substructure property.
• ?????

0-1 knapsack problem
• The setup is the same, but the items may not be broken into smaller
pieces, so thief may decide either to take an item or to leave it
(binary choice), but may not take a fraction of an item.Exhibit No
greedy choice property.
• No greedy algorithm exists.
• Exhibit optimal substructure property.
• Only dynamic programming algorithm exists.

Greedy Solution - Fractional Knapsack Problem
• There are n items in a store. For i =1,2, . . . , n, item i has weight wi >
0 and worth vi> 0. Thief can carry a maximum weight of W pounds in a
knapsack.
• In this version of a problem the items can be broken into smaller piece, so
the thief may decide to carry only a fraction xi of object i, where 0 ≤ xi ≤
1. Item i contributes xiwi to the total weight in the knapsack, and xivi to
the value of the load.
• In Symbol, the fraction knapsack problem can be stated as follows.
maximize nSi=1 xivi subject to constraint nSi=1 xiwi ≤ W
• It is clear that an optimal solution must fill the knapsack exactly, for
otherwise we could add a fraction of one of the remaining objects and
increase the value of the load. Thus in an optimal solution nSi=1 xiwi = W.

The knapsack problem
• n objects, each with a weight wi > 0
a profit pi > 0
capacity of knapsack: M
Maximize
Subject to
0  xi  1, 1  i  n
p xi i
i n1 

w x Mi i
i n1 
 

The knapsack Pseudo Code
• The greedy algorithm:
Step 1: Sort pi/wi into nonincreasing order.
Step 2: Put the objects into the knapsack according
to the sorted sequence as possible as we can.

Algorithm
Greedy-fractional-knapsack (w, v, W)
FOR i =1 to do
x[i] =0
weight = 0
while weight < W do
i = best remaining item
IF weight + w[i] ≤ W then
x[i] = 1
weight = weight + w[i]
else
x[i] = (w - weight) / w[i]
weight = W
return x

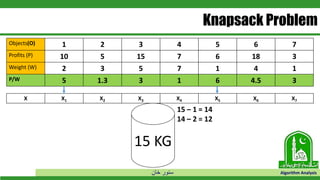
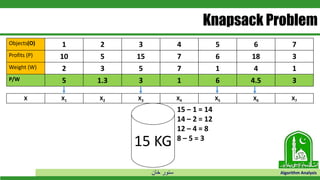
Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
15 KG

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
15 KG
X X1 X2 X3 X4 X5 X6 X7

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
P/W 5 1.3 3 1 6 4.5 3
15 KG
X X1 X2 X3 X4 X5 X6 X7

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
P/W 5 1.3 3 1 6 4.5 3
15 KG
X X1 X2 X3 X4 X5 X6 X7
15 – 1 = 14

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
P/W 5 1.3 3 1 6 4.5 3
15 KG
X X1 X2 X3 X4 X5 X6 X7
15 – 1 = 14
14 – 2 = 12

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
P/W 5 1.3 3 1 6 4.5 3
15 KG
X X1 X2 X3 X4 X5 X6 X7
15 – 1 = 14
14 – 2 = 12
12 – 4 = 8

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
P/W 5 1.3 3 1 6 4.5 3
15 KG
X X1 X2 X3 X4 X5 X6 X7
15 – 1 = 14
14 – 2 = 12
12 – 4 = 8
8 – 5 = 3

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
P/W 5 1.3 3 1 6 4.5 3
15 KG
X X1 X2 X3 X4 X5 X6 X7
15 – 1 = 14
14 – 2 = 12
12 – 4 = 8
8 – 5 = 3
3 – 1 = 2

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
P/W 5 1.3 3 1 6 4.5 3
15 KG
X X1 X2 X3 X4 X5 X6 X7
15 – 1 = 14
14 – 2 = 12
12 – 4 = 8
8 – 5 = 3
3 – 1 = 2
2 – 2 = 0
2 /3

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
P/W 5 1.3 3 1 6 4.5 3
15 KG
X X1 X2 X3 X4 X5 X6 X7
15 – 1 = 14
14 – 2 = 12
12 – 4 = 8
8 – 5 = 3
3 – 1 = 2
2 – 2 = 0
2 /3 0

Knapsack Problem
Objects(O) 1 2 3 4 5 6 7
Profits (P) 10 5 15 7 6 18 3
Weight (W) 2 3 5 7 1 4 1
P/W 5 1.3 3 1 6 4.5 3
X X1 X2 X3 X4 X5 X6 X7
2 /3 0
Calculate Weight
σ 𝑥𝑖 𝑤 𝑖= 1 𝑥 2 + 2/3 𝑥 3 + 1 𝑥 5 + 0 𝑥 7 + 1 𝑥 1 + 1 𝑥 4 + 1 𝑥 1
2 + 2 + 5 + 0 + 1 + 4 + 1 = 15
Calculate Profit
෍ 𝑥𝑖 𝑝 𝑖= 1 𝑋 10 +
2
3𝑥5
+ 1𝑥5 + 1𝑥6 + 1𝑥18 + 1𝑥3
10 + 2𝑥1.3 + 15 + 6 + 18 + 3 = 54.6

Conclusion
•Constraints
σ 𝑥𝑖 𝑤𝑖 ≤ m where m = 15
•Objective
𝑀𝐴𝑋 ෍ 𝑥𝑖 𝑝 𝑖=

Analysis
• If the items are already sorted into decreasing order of vi / wi, then
the while-loop takes a time in O(n);
Therefore, the total time including the sort is in O(n log n).
• If we keep the items in heap with largest vi/wi at the root. Then
• creating the heap takes O(n) time
• while-loop now takes O(log n) time (since heap property must be restored
after the removal of root)
• Although this data structure does not alter the worst-case, it may be
faster if only a small number of items are need to fill the knapsack.

Greedy algorithm

More Related Content

What's hot (20)

Similar to Greedy algorithm (20)

More from International Islamic University (20)

Recently uploaded (20)

Greedy algorithm