Introduction to Monte Carlo Ray Tracing (CEDEC 2013)

モンテカルロレイトレーシングの基礎から
OpenCLによる実装まで
TAKAHIRO HARADA

2モンテカルロレイトレーシングの基礎からOpenCLによる実装まで | AUG, 2013
レイトレーシング
} ラスタライゼーション
–  トライアングルを順番に画面に貼って行く
–  DX, OpenGL
} レイトレーシング
–  もう一つのレンダリング方法
–  ピクセルの色を順番に求める
} リアルタイムグローバルイルミネーション
–  近年Hot
–  モンテカルロレイトレーシングは”the solution”
–  リアルタイムアルゴリズムを考える上で知っておくことは重要
•  リアルタイム化 == これをどう簡略化するか

MOTIVATION
} GI (MCRT) looks scary
–  PBRT本は重すぎ…
–  数式多すぎ…
•  Search for “Monte Carlo Integration”, “Importance
Sampling” on Wikipedia
} 本セッション
–  より直感的な理解を
–  Give more intuitive understanding
–  Not for PBRT lovers
–  Not for equation lovers

AGENDA
} Basic Topics
} Advanced Topics
} OpenCL Implementation

FIND VISIBLE POINT
} ピクセルごとにレイを生成
} レイが表面にぶつかった点のうち最も近いものを見つける
} Brute-force
–  全てのトライアングルに対して
•  t_min = min2( t_min, intersect( ray, tri[i] ) )
–  効率が悪い
} 空間分割を導入することで効率化可能
–  Bounding Volume Hierarchy (BVH)

MAJOR SURFACE TYPES

REFLECTION (SPECULAR)
} 鏡面反射
} 出射する光の強さ == 入射する光の強さ*
θi = θo
* フレネルを除くと

} 鏡面反射
θi = θo

REFRACTION (SPECULAR)
} Transmission
} 光が表面で方向を変える
} スネルの法則 (Snell’s law)
} 実際は反射も起こる
ηi sin θi = ηo sin θo

REFRACTION + REFLECTION
} どのような透明な物体でも表面で光を反射させる
} 屈折と反射の割合
–  フレネル効果 (Fresnel)
–  屈折率

FRESNEL
} 割合は一様ではない
} 視線ベクトルと表面の法線ベクトルの角度
–  平行ならば
•  屈折が強い
–  垂直ならば
•  反射が強い
Reflection
Refraction
Reflection
Refraction
<
<

FRESNEL
} 割合は一様ではない
} 視線ベクトルと表面の法線ベクトルの角度
–  平行ならば
•  屈折が強い
–  垂直ならば
•  反射が強い
} Schlick’s approximation
Schlick
View : Normal
= Orthogonal
View : Normal
= Parallel
　Small IOR 　Large IOR

REFRACTION + REFLECTION
} 表面で二本のレイをキャスト*
–  反射のレイ
–  屈折のレイ
* レイの数が増えすぎる問題はあるが

} 鏡面反射
} 出射する光の強さ == 入射する光の強さ x フレネル
θi = θo

} レイトレーシング
} モンテカルロレイトレーシング

MAJOR SURFACE TYPES

MATT
} Lambert
} Oren Nayar
–  よりMattな表面

MATT
} Lambert
} 表面に当たった光は全ての方向に反射
} ある方向に出て行く光は全ての方向から入ってきた光で決まる

MATT
} Lambert
} どうやって全ての方向から入射する光を求める?

MATT
} Lambert
–  光源が占める角度を知りたい
–  点光源の場合は簡単

MATT
} Lambert
–  点光源の場合は簡単
–  面光源の場合は?
•  Monte Carlo Integration!

INTEGRATE INCOMING LIGHT
} どれだけの光が半球から入ってくるか?
} Q: 光源の占める角度を知りたい

IDEA
} 半球を分割
} それぞれの領域について光源があるかチェック

IDEA
} 半球を分割
} それぞれの領域について光源があるかチェック
} それぞれの領域にレイを飛ばす
–  Sampleを生成する

IDEA
} 8本のレイ(sample)のうち2本ヒット
} 半球の約2/8が光源に覆われていると推測できる
} 定式化は
–  単位半球上の面積 (3D)
–  単位半円上の長さ (2D)
•  割合 x 円周 =
2
8
π

IDEA
}  半球を分割
}  それぞれの領域について光源があるかチェック
–  8 samples
}  サンプルの重み (正規化)
}  2ヒット
(== ratio to total length)
}  単位半円の円周 (2D)
}  光源の面積
Flatten
π ×
2
8
= π
i<8
∑
i=0
1
8
L(i) = π
i<8
∑
i=0
wiL(i)
wi =
1
8
,
∑
wi = 1
π =
∫Ω
dω
2
8
≈
∫Ω
L(ω)dω

MOTE CARLO INTEGRATION
}  ランダムなレイ(sample) を引く (Draw)
}  サンプルが光源に当たるかチェック
–  8 samples
}  サンプルの重み
}  2ヒット
}  光源の面積
–  総サンプル数で割る (正規化)
Flatten
wi = π,
∑
wi = 8π
2π
1
8
× 2π =
2
8
π

MONTE CARLO INTEGRATION
} A numerical integration suited for
–  Integration of a complex high dimensional function
} Draw a random sample
} Calculate a weighted average
∫Ω
L(ω)dω ≈
i<8
∑
i=0
wiLi
=
1
n
i<n
∑
i=0
Li
pdfi
pdfi =
1
π
, n = 8
Formula we see in a textbook

MATT
} Lambert

MATT SURFACE EVALUATION
Ray0 Ray1 Ray2 Ray3 Ray4 Ray5 Ray6 Ray7
Hit? 0 0 0 0 0 0 1 1
Brdf 1/pi 1/pi 1/pi 1/pi 1/pi 1/pi 1/pi 1/pi
cos(n,l) c0 c1 c2 c3 c4 c5 c6 c7
Li(ωi) =
∫Ω
fwhiteLi(ωi)cos θdω
(
1
π
c6 +
1
π
c7)
π
8
∫Ω
L(ω)dω
+
x x x x x x x x

WHERE PI COMES FROM?
} Lambert
} Distribute energy uniformly
} Pure white surface
–  Incoming light == sum of outgoing light (reflected
light)
} BRDF for a Lambert surface
flambert(x, ωi, ωo) =
R
π
Li(ωi) =
∫Ω
fwhiteLi(ωi)cos θdω fwhite =
1
π
==
Incoming light Sum of reflected light
The image cannot be displayed. Your computer may not have enough memory to open the
image, or the image may have been corrupted. Restart your computer, and then open the ﬁle
again. If the red x still appears, you may have to delete the image and then insert it again.

REFLECTION SURFACE EVALUATION
Hit? 0 0 0 0 0 0 1 1
Brdf 0 0 0 0 0 0 0 b7
(b7c7)
π
8
+
x x x x x x x x

GLOSSY
} Microfacet
} 様々なglossinessを表現できる
–  鋭いspecularに近いものから鈍いmattに近いものまで

GLOSSY
} Microfacet
} Torrance-Sparrowモデル
–  表面の法線は分散を持っている (Distribution) D
–  フレネル F
–  表面自体のocclusion G
Wide distribution Mid distribution Narrow distribution
fmf (n, l, e) =
DFG
4 cos(n, l)cos(n, e)

GLOSSY (MICROFACET)
} Microfacet
} Torrance-Sparrowモデル
–  表面の法線は分散を持っている (Distribution) D
–  フレネル F
–  表面自体のocclusion G

GLOSSY SURFACE EVALUATION
Hit? 0 0 0 0 0 0 1 1
Brdf b0 b1 b2 b3 b4 b5 b6 b7
(b6c6 + b7c7)
π
8
+
x x x x x x x x

ADVANCED TOPICS
}  Why noisy result?
}  Better sampling
}  How can we make a realistic material?
}  Complex materials
}  Want to have light bounce
}  Indirect illumination
}  Where are nice effects?
}  Distributed ray tracing

NOISE REDUCTION
(IMPORTANCE SAMPLING)

BETTER SAMPLING
} ノイズはどこから?
} Monte Carlo Integrationを使っているから
–  サンプルの数が十分ではない
–  ランダムサンプリング
–  サンプルの取り方の小さな違い
•  => 異なった結果

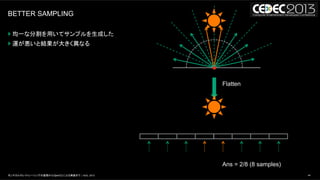
BETTER SAMPLING
} 均一な分割を用いてサンプルを生成した
} 運が悪いと結果が大きく異なる
Flatten
Ans = 2/8 (8 samples)

BETTER SAMPLING
} 均一な分割を用いてサンプルを生成した
} 運が悪いと結果が大きく異なる
} どうにか改善できないか?
–  もし光源の場所がわかっていたら?
Flatten
Ans = 1/8 (8 samples)

BETTER SAMPLING
} 均一ではないスプリット
} 重みを変える必要がある
} より多くのサンプルを光源方向に
–  6 samples, w = 1/16
–  2 samples, w = 5/16
} 光源の面積 Flatten
Ans = 3/16 pi (8 samples)
1/165/16
1
16
× 3 × π =
3
16
π

BETTER SAMPLING
} 均一ではないスプリット
} 重みを変える必要がある
} より多くのサンプルを光源方向に
–  4 samples, w = 1/16
–  2 samples, w = 6/16
} 光源の面積
} サンプル数を減らしたけど同じ結果
–  精度の向上
} Importance sampling
–  より多くのサンプルをターゲットの周辺に
–  重みを修正 (pdfを上げる、下げる)
–  ライトサンプリング
Flatten
Ans = 3/16 pi (6 samples)
1/166/16
1
16
× 3 × π =
3
16
π

IMPORTANCE SAMPLING EXAMPLE
Uniform Sampling Light Sampling

LIGHT SAMPLING ENOUGH?
Matt Surface
} ライトサンプリングが有効
Glossy Surface
} ライトサンプリングが有効ではない
} BRDFの値の大きい方向にサンプルを生成した方が
よい
–  BRDFサンプリング

IMPORTANCE SAMPLING
} ライトサンプリング
} BRDFサンプリング
} Multiple importance sampling
–  Sample light, but adjust weight by BRDF distribution
–  Sample BRDF, but adjust weight by Light distribution
better >>>> worse
worse <<<< better

LITTLE BIT MORE ABOUT MATT
} どんなMattな表面でも光を鏡面反射している
–  紙でも
–  完全な拡散だけではない
–  ある程度の光が鏡面反射し、ある程度の光が拡散
} 見る角度によって反射が変わる?

REALISTIC MATT MATERIAL
–  紙でも
–  表面でフレネルの効果が起こっている
–  物体の屈折率 (ior)

–  紙でも
–  表面でフレネルの効果が起こっている
–  物体の屈折率 (ior)
–  透明な物体の反射屈折に似ている

WHAT IS MATT SURFACE??
} どんな表面でも光は鏡面反射
} 反射しなかった光は内部に屈折
–  散乱せずに直進するのが純粋な屈折
–  Mattな表面は屈折した光が散乱してどの方向にも均等に出て行く

} モデル化
–  2 layer model
–  1st layer: Specular
–  2nd layer: Matt
} Spec x (1-f) + Matt x f
–  f == Fresnel
1-f
f

WHAT WE HAVE SO FAR
} いくつかのBRDFモデルのみ
} どの表面でもフレネル効果が現れている
} これらだけでリアルなマテリアルの表現ができるのか?
Specular (R) Glossy MattSpecular (T)

COMPLEX MATERIAL EXAMPLES

WOOD TILE
} 2レイヤーモデル
–  Glossy
–  Matt
} Glossy x (1-f) + Matt x f
1-f
f

WOOD TILE
–  Glossy
–  Matt
} Glossy x (1-f) + Matt x f
1-f
f
x (1-f) + x f

CARBON FIBER
–  Specular
–  Glossy
–  Matt
1-f
f
1-f
f

Matt Glossy M+G M+G+Specular

SOMETHING
–  Specular
–  Refraction
–  Glossy
–  Matt
1-f
f
1-f
f
1-f
f

Matt + Glossy Transparent M+G+T M+G+T+Specular

MATERIAL DESCRIPTION
} fres(G, M)
} fres(S, mix(G, M, 0.5))
} fres(S, add(T, fres(G, M)))

COMPARISON
Direct Illumination Indirect Illumination

INDIRECT ILLUMINATION
} ダイレクトイルミネーション
–  半球上から入射する光の総和を推測
–  8サンプル (レイ)
–  ライトに当たったサンプルは0でない値

INDIRECT ILLUMINATION
} インダイレクトイルミネーション
–  半球上から入射する光の総和を推測
–  8サンプル (レイ)
–  物体に当たったサンプルは0でない値
} 表面から来る光はどのくらい?
??

LIGHT FROM SURFACE
} 表面から届く光はダイレクトイルミネーションの計算と
同じように行うことができる
We were solving this We want to solve this

SOLUTION 1
} 8サンプル (レイを飛ばす)
} 8サンプルの値の重み付け和を求める
} .
} 欠点
–  キャストするレイの数が急激に増加
•  レイの総数 = プライマリレイの数 x 8 x 8
•  高い解像度でのレンダリング
•  アンチエイリアシング
–  2バウンド以上だとレイの数が指数関数的に増加
•  バウンドの多いレンダリングに不向き
wi =
π
8
Lo(ωo) ≈
∑
π
8
f(x, n, ωi)Li(ωi)cos(n, ωi)
Lo(ωo) ≈
∑
π
8

SOLUTION 1
} 1サンプル
} その値だけを用いて光の総和を推定
} .
} 利点
–  飛ばすレイの数が少ない
–  バウンドの多いレンダリングに向いている
} 欠点
–  ノイジーな結果
–  ノイズを減らすため多くのサンプルを生成する必要がある
} 一般的なパストレーシング
–  レイのバウンドが終わるまで追っていく
Lo(ωo) ≈
∑
π
8
Lo(ωo) ≈
π
1
wi =
π
1

SO FAR
} Monte Carlo Integrationを半球上の入射光の積分に用いた
} Monte Carlo Integrationを他の積分に用いる
–  レンズ
–  時間

OTHER EFFECTS
Depth of Field (Integrate over lens) Motion blur (Integrate over time)

MC RT IS SLOW!
} Computation takes a long time
–  Monte Carlo ray tracing need to cast a lot of rays/pixel
} Slow iteration
–  Inefficient development
–  Cannot test a lot
} If we can make it faster, we can
–  Test more
•  Software reliability
–  Go further
•  Better algorithm
} Computer history == Make it faster!
} Options
–  Algorithm improvement
–  Exploit hardware

WHY OPENCL?
} Using OpenCL is equivalent to
–  Efficient usage of computational resources
–  Use GPU
–  Use multi-core CPU more efficiently
} GPU has high peak performance
–  AMD Radeon HD 7970　(GCN Architecture)
•  3.8 TFLOPS (S)
•  974 GFLOPS (D)
•  264 GB/s
–  Parallel computation
•  128 SIMD engines
–  64 wide SIMD

OPENCL
} Open Compute Language (OpenCL) for parallel processors (including GPU)
} OpenCL 1.0 specification released in 2008
} Now v1.2
} ISO C99 with extensions and restrictions
} Software portability
–  Cross platform support
•  Windows, Mac, Linux
–  Multi device support
•  GPU
–  AMD, NVIDIA, Intel
•  CPU
•  etc
–  Write once, run on all the supported
} Direct Compute
–  Need DX
–  GPU only

CPU VECTOR ADD
} CPU code is simple
float* a = new float[n];
float* b = new float[n];
float* c = new float[n];
for(int i=0; i<n; i++)
{
b[i] = i;
c[i] = n;
}
{
a[i] = b[i] + c[i];
}
delete [] a;
delete [] b;
delete [] c;
Memory allocation
Initialization
Computation
Memory deallocation

TO IMPLEMENT USING OPENCL
} Need to do 3 things
1.  OpenCL memory has to be allocated, deallocated
2.  Computation has to be written as OpenCL kernel
3.  OpenCL kernel has to be executed via OpenCL APIs

MEMORY ALLOCATION/DEALLOCATION
} CPU
–  Allocation
–  Deallocation
} OpenCL
–  Allocation
–  Deallocation
delete [] a;
cl_mem a = clCreateBuffer( context, CL_MEM_READ_WRITE, sizeof(float)*n, 0, &e );
clReleaseMemObject( a );
Memory size in byte

COMPUTE USING OPENCL KERNEL
} CPU
–  n items are executed in serial
} OpenCL
–  n items are executed in parallel
–  A work item processes an item
–  Write program (OpenCL Kernel) for a work item
–  Not in the host C code
{
a[i] = b[i] + c[i];
}
__kernel
void addKernel( __global float* a,
__global float* b,
__global float* c )
{
int i = get_global_id(0);
a[i] = b[i] + c[i];
}
__global : for a memory allocated in global memory
__local : for a memory allocated in local memory
Can use the code for computations in this pattern

EXECUTE OPENCL KERNEL
} Set OpenCL memories as arguments
–  Specify the index of the argument
} Execute kernel
clSetKernelArg(kernel1, 0, sizeof(cl_mem), (void*)&a);
clSetKernelArg(kernel1, 1, sizeof(cl_mem), (void*)&b);
clSetKernelArg(kernel1, 2, sizeof(cl_mem), (void*)&c);
clEnqueueNDRangeKernel( queue, kernel1, 1, 0, gSize, lSize, 0, 0, 0 );
__kernel
__global float* b,
__global float* c )
{
a[i] = b[i] + c[i];
}
Order of an argument
Work group size [64, 1, 1]
Global work size [n,1,1]

OPENCL VECTOR ADD
__kernel
void initKernel( __global float* b,
__global float* c )
{
b[i] = i;
c[i] = i;
}
__kernel
__global float* b,
__global float* c )
{
a[i] = b[i] + c[i];
}
cl_mem a = clCreateBuffer( context, CL_MEM_READ_WRITE, sizeof(float)*n, 0, &e );
cl_mem b = clCreateBuffer( context, CL_MEM_READ_WRITE, sizeof(float)*n, 0, &e );
cl_mem c = clCreateBuffer( context, CL_MEM_READ_WRITE, sizeof(float)*n, 0, &e );
clReleaseMemObject( b );
clReleaseMemObject( c );
Memory allocation
Initialization
Computation
Memory deallocation

CODE COMPARISON
CPU OpenCL
float* b = new float[n];
float* c = new float[n];
{
b[i] = i;
c[i] = n;
}
{
a[i] = b[i] + c[i];
}
delete [] a;
delete [] b;
delete [] c;
cl_mem a = clCreateBuffer( context, CL_MEM_READ_WRITE, siz
cl_mem b = clCreateBuffer( context, CL_MEM_READ_WRITE, siz
cl_mem c = clCreateBuffer( context, CL_MEM_READ_WRITE, siz
clEnqueueNDRangeKernel( queue, kernel0, 1, 0, gSize, lSize
clEnqueueNDRangeKernel( queue, kernel1, 1, 0, gSize, lSize
clReleaseMemObject( b );
clReleaseMemObject( c );
Memory allocation
Initialization
Computation
Memory deallocation

IMPLEMENT DIRECT LIGHTING
} Generate ray
} Cast ray
} Generate sample ray
} Cast shadow ray
} Accumulate result

SINGLE KERNEL IMPLEMENTATION
} Describe everything in a kernel
} Pros
–  Easy to implement
•  Straightforward port from CPU implementation
} Cons
–  Poor HW utilization
–  Divergence
–  Register pressure
Host:
executeKernel(SingleKernel);
Device:
__kernel
void SingleKernel()
{
while( i < maxSamples )
{
GenerateRay();
CastRay();
if( hit )
{
GenerateSampleRay();
CastShadowRay();
AccumulateResult();
}
}
}

DIVERGENCE
} 1st
–  Generate Ray
–  Cast Ray
–  Generate Sample Ray
–  Cast Shadow Ray
–  Accumulate Result

MULTIPLE KERNEL IMPLEMENTATION
} Split the pipeline into multiple kernels
} Pros
–  Better HW utilization
–  More room for optimization
} Cons
–  Need more work than single kernel implementation
–  Host has to queue more OpenCL commands
–  Each kernel has to read/write ray info
Host:
while( i < maxSamples )
{
executeKernel(RayGenerationKernel);
executeKernel(RayCastKernel);
executeKernel(SampleRayKernel);
executeKernel(RayCastKernel);
executeKernel(AccumulationKernel);
}
Device:
__kernel
void RayCastKernel()
{
}

DIVERGENCE
} 1st
–  Generate Ray
–  Cast Ray

DIVERGENCE 2 BOUNCES
} 1st
–  Generate Ray
–  Cast Ray
} 2st
–  Generate Ray
–  Cast Ray

DIVERGENCE
} 1st
–  Generate Ray
–  Cast Ray
} 2st
–  Generate Ray
–  Cast Ray

TIPS
} Starting
–  Single kernel implementation
–  Share data types with host (float4)
•  Easy to share functions
–  Replace pointers to indices
} Debugging
–  Printf
–  Debug buffers
} Others
–  Cache compiled kernel
•  Reduce compilation time
Coumans, E., Multithreading and VFX Course note, SIGGRAPH 2013

EXAMPLES
} All figures in this presentation are generated by an OpenCL renderer
–  Radeon HD 7970

WHAT IS COVERED
} BRDF
–  Reflection, refraction, glossy, matt
} Fresnel
} Monte Carlo Integration
–  Direct Illumination
–  Indirect Illumination
} Importance Sampling
–  Light sampling
–  BRDF sampling
} Layered Materials
} OpenCL Introduction
} Tips for OpenCL implementation

Introduction to Monte Carlo Ray Tracing (CEDEC 2013)

More Related Content

What's hot (20)

More from Takahiro Harada (17)

Recently uploaded (9)

Introduction to Monte Carlo Ray Tracing (CEDEC 2013)