![Intro ECA KECA Clustering Results Conclusions
Objectives
Objectives
Kernel-based non-linear data-transformation
Captures the data higher order statistics
Extracts features suited for clustering
Method
Kernel Entropy Component Analysis (KECA) [Jenssen, 2010]
Based on Information Theory:
Maximally preserves entropy of the input data
Angular clustering maximizes cluster divergence
Out-of-sample extension to deal with test data
Experiments
Cloud screening from ENVISAT/MERIS multispectral images
L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 3/26](https://image.slidesharecdn.com/kernel-entropy-component-analysis-in-remote-sensing-data-clustering-110728022713-phpapp02/85/Kernel-Entropy-Component-Analysis-in-Remote-Sensing-Data-Clustering-pdf-4-320.jpg)
![Intro ECA KECA Clustering Results Conclusions
Kernel Principal Component Analysis (KPCA)
Principal Component Analysis (PCA)
Find projections of X = [x1 , . . . , xN ] maximizing the variance of data XU
PCA: maximize: Trace{(XU) (XU)} = Trace{U Cxx U}
subject to: U U=I
Including Lagrange multipliers λ, this is equivalent to the eigenproblem
Cxx ui = λi ui → Cxx U = UD
ui are the eigenvectors of Cxx and they are orthonormal, ui uj = 0
PCA
L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 12/26](https://image.slidesharecdn.com/kernel-entropy-component-analysis-in-remote-sensing-data-clustering-110728022713-phpapp02/85/Kernel-Entropy-Component-Analysis-in-Remote-Sensing-Data-Clustering-pdf-13-320.jpg)
![Intro ECA KECA Clustering Results Conclusions
Kernel Principal Component Analysis (KPCA)
Kernel Principal Component Analysis (KPCA)
Find projections maximizing variance of mapped data [φ(x1 ), . . . , φ(xN )]
KPCA: maximize: Tr{(ΦU) (ΦU)} = Tr{U Φ ΦU}
subject to: U U=I
The covariance matrix Φ Φ and projection matrix U are dH × dH !!!
KPCA through kernel trick
Apply the representer’s theorem: U = Φ A where A = [α1 , . . . , αN ]
KPCA: maximize: Tr{A ΦΦ ΦΦ A} = Tr{A KKA}
subject to: U U = A ΦΦ A = A KA = I
Including Lagrange multipliers λ, this is equivalent to the eigenproblem
KKαi = λi Kαi → Kαi = λi αi
Now matrix A is N × N !!! (eigendecomposition of K = EDE = AA )
L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 13/26](https://image.slidesharecdn.com/kernel-entropy-component-analysis-in-remote-sensing-data-clustering-110728022713-phpapp02/85/Kernel-Entropy-Component-Analysis-in-Remote-Sensing-Data-Clustering-pdf-14-320.jpg)
Kernel Entropy Component Analysis in Remote Sensing Data Clustering.pdf
- 1. Kernel Entropy Component Analysis in Remote Sensing Data Clustering Luis Gómez-Chova1 Robert Jenssen2 Gustavo Camps-Valls1 1 Image Processing Laboratory (IPL), Universitat de València, Spain. [email protected] , http://www.valencia.edu/chovago 2 Department of Physics and Technology, University of Tromsø, Norway. [email protected] , http://www.phys.uit.no/∼robertj IGARSS 2011 – Vancouver, Canada * IPL Image Processing Laboratory
- 2. Intro ECA KECA Clustering Results Conclusions Outline 1 Introduction 2 Entropy Component Analysis 3 Kernel Entropy Component Analysis (KECA) 4 KECA Spectral Clustering 5 Experimental Results 6 Conclusions and Open questions L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 1/26
- 3. Intro ECA KECA Clustering Results Conclusions Motivation Feature Extraction Feature selection/extraction essential before classification or regression to discard redundant or noisy components to reduce the dimensionality of the data Create a subset of new features by combinations of the existing ones Linear Feature Extraction Offer Interpretability ∼ knowledge discovery PCA: projections maximizing the data set variance PLS: projections maximally aligned with the labels ICA: non-orthogonal projections with maximal independent axes Fail when data distributions are curved Nonlinear feature relations L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 2/26
- 4. Intro ECA KECA Clustering Results Conclusions Objectives Objectives Kernel-based non-linear data-transformation Captures the data higher order statistics Extracts features suited for clustering Method Kernel Entropy Component Analysis (KECA) [Jenssen, 2010] Based on Information Theory: Maximally preserves entropy of the input data Angular clustering maximizes cluster divergence Out-of-sample extension to deal with test data Experiments Cloud screening from ENVISAT/MERIS multispectral images L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 3/26
- 5. Intro ECA KECA Clustering Results Conclusions 1 Introduction 2 Entropy Component Analysis 3 Kernel Entropy Component Analysis (KECA) 4 KECA Spectral Clustering 5 Experimental Results 6 Conclusions and Open questions L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 4/26
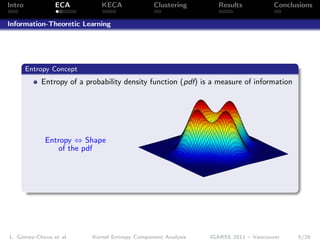
- 6. Intro ECA KECA Clustering Results Conclusions Information-Theoretic Learning Entropy Concept Entropy of a probability density function (pdf) is a measure of information Entropy ⇔ Shape of the pdf L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 5/26
- 7. Intro ECA KECA Clustering Results Conclusions Information-Theoretic Learning Divergence Concept The entropy concept can be extended to obtain a measure of dissimilarity between distributions ←→ Divergence ⇔ Distance between pdfs L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 6/26
- 8. Intro ECA KECA Clustering Results Conclusions Entropy Component Analysis Shannon entropy Z H(p) = − p(x) log p(x)dx How to handle densities? How to compute integrals? Rényi’s entropies Z 1 H(p) = − log p α (x)dx 1−α Rényi’s entropies contain Shannon as a special case α → 1 We focus on the Rényi’s quadratic entropy α = 2 Rényi’s quadratic entropy Z H(p) = − log p 2 (x)dx = − log V (p) It can be estimated directly from samples! L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 7/26
- 9. Intro ECA KECA Clustering Results Conclusions Entropy Component Analysis Rényi’s quadratic entropy estimator Estimated from data D = {x1 , . . . , xN } ∈ Rd generated by the pdf p(x) Parzen window estimator with a Gaussian or Radial Basis Function (RBF): 1 X 2 K (x, xt | σ) /2σ 2 ` ´ p (x) = ˆ with K (x, xt ) = exp − x − xt N x ∈D t Idea: Place a kernel over the samples and sum with proper normalization The estimator for the information potential V (p) = p 2 (x)dx R Z Z 1 X 1 X ˆ V (p) = p 2 (x)dx = ˆ K (x, xt | σ) K (x, xt | σ)dx N x ∈D N x ∈D t t Z 1 X X = K (x, xt | σ)K (x, xt | σ)dx N 2 x ∈D x ∈D t t 1 X X √ 1 = 2 K (xt , xt | 2σ) = 2 1 K1 N x ∈D x ∈D N t t L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 8/26
- 10. Intro ECA KECA Clustering Results Conclusions Entropy Component Analysis Rényi’s quadratic entropy estimator Empirical Rényi entropy estimate resides in the corresponding kernel matrix ˆ 1 V (p) = 2 1 K1 N It can be expressed in terms of eigenvalues and eigenvectors of K D diagonal matrix of eigenvalues λ1 , . . . , λN K = EDE E matrix with the eigenvectors e1 , . . . , eN Therefore we then have N 1 X “p ”2 ˆ V (p) = 2 λi ei 1 N i =1 √ where each term λi ei 1 will contribute to the entropy estimate ECA dimensionality reduction Idea: to find the smallest set of features √ maximally preserve the that entropy of the input data (contributions λi ei 1) L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 9/26
- 11. Intro ECA KECA Clustering Results Conclusions Entropy Component Analysis H(p) = 4.36 H(p) = 4.74 H(p) = 5.05 H(p) = 4.71 ˆ H(p) = 4.81 , H(p) = 4.44 L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 10/26
- 12. Intro ECA KECA Clustering Results Conclusions 1 Introduction 2 Entropy Component Analysis 3 Kernel Entropy Component Analysis (KECA) 4 KECA Spectral Clustering 5 Experimental Results 6 Conclusions and Open questions L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 11/26
- 13. Intro ECA KECA Clustering Results Conclusions Kernel Principal Component Analysis (KPCA) Principal Component Analysis (PCA) Find projections of X = [x1 , . . . , xN ] maximizing the variance of data XU PCA: maximize: Trace{(XU) (XU)} = Trace{U Cxx U} subject to: U U=I Including Lagrange multipliers λ, this is equivalent to the eigenproblem Cxx ui = λi ui → Cxx U = UD ui are the eigenvectors of Cxx and they are orthonormal, ui uj = 0 PCA L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 12/26
- 14. Intro ECA KECA Clustering Results Conclusions Kernel Principal Component Analysis (KPCA) Kernel Principal Component Analysis (KPCA) Find projections maximizing variance of mapped data [φ(x1 ), . . . , φ(xN )] KPCA: maximize: Tr{(ΦU) (ΦU)} = Tr{U Φ ΦU} subject to: U U=I The covariance matrix Φ Φ and projection matrix U are dH × dH !!! KPCA through kernel trick Apply the representer’s theorem: U = Φ A where A = [α1 , . . . , αN ] KPCA: maximize: Tr{A ΦΦ ΦΦ A} = Tr{A KKA} subject to: U U = A ΦΦ A = A KA = I Including Lagrange multipliers λ, this is equivalent to the eigenproblem KKαi = λi Kαi → Kαi = λi αi Now matrix A is N × N !!! (eigendecomposition of K = EDE = AA ) L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 13/26
- 15. Intro ECA KECA Clustering Results Conclusions Kernel ECA Transformation Kernel Entropy Component Analysis (KECA) KECA: projection of Φ onto those m feature-space principal axes contributing most to the Rényi entropy estimate of the input data 1 2 Φeca = ΦUm = Em Dm √ Projections onto a single principal axis ui in H is given by ui Φ = λi ei 1 1 Pm `√ ´2 ˆ Entropy associated with Φeca is Vm = N 2 1 Keca 1 = N 2 λi ei 1 i =1 Note that Φeca is not necessarily based on the top eigenvalues λi since ei 1 also contributes to the entropy estimate Out-of-sample extension Projections for a collection of test data points: −1 −1 Φeca,test = Φtest Um = Φtest ΦEm Dm 2 = Ktest Em Dm 2 L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 14/26
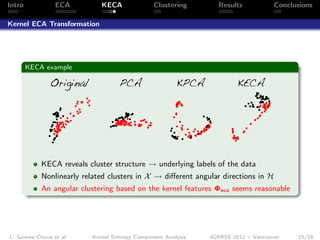
- 16. Intro ECA KECA Clustering Results Conclusions Kernel ECA Transformation KECA example Original PCA KPCA KECA KECA reveals cluster structure → underlying labels of the data Nonlinearly related clusters in X → different angular directions in H An angular clustering based on the kernel features Φeca seems reasonable L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 15/26
- 17. Intro ECA KECA Clustering Results Conclusions 1 Introduction 2 Entropy Component Analysis 3 Kernel Entropy Component Analysis (KECA) 4 KECA Spectral Clustering 5 Experimental Results 6 Conclusions and Open questions L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 16/26
- 18. Intro ECA KECA Clustering Results Conclusions KECA Spectral Clustering Cauchy-Schwarz divergence The Cauchy-Schwarz divergence between the pdf of two clusters is R pi (x)pj (x)d x DCS (pi , pj ) = − log(VCS (pi , pj )) = − log qR R pi (x)d x pj2 (x)d x 2 Measuring dissimilarity in a probability space is a complex issue 1 φ(xt ): P Entropy interpretation in the kernel space → mean vector µ = N Z 1 1 V (p) = p 2 (x)dx = 2 1 K1 = 2 1 ΦΦ 1 = µ µ = µ 2 ˆ ˆ N N µi µj Diverg. via Parzen windowing ⇒ VCS (pi , pj ) = ˆ µi µj = cos ∠(µi , µj ) KECA Spectral Clustering Angular clustering of Φeca maximizes the CS divergence between clusters: k X J(C1 , . . . , Ck ) = Ni cos ∠(φeca (x), µi ) i =1 L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 17/26
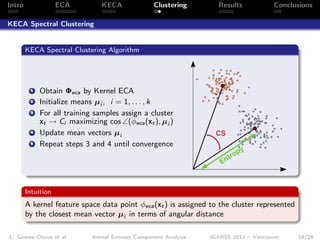
- 19. Intro ECA KECA Clustering Results Conclusions KECA Spectral Clustering KECA Spectral Clustering Algorithm 1 Obtain Φeca by Kernel ECA 2 Initialize means µi , i = 1, . . . , k 3 For all training samples assign a cluster xt → Ci maximizing cos ∠(φeca (xt ), µi ) 4 Update mean vectors µi CS 5 Repeat steps 3 and 4 until convergence py tro En Intuition A kernel feature space data point φeca (xt ) is assigned to the cluster represented by the closest mean vector µi in terms of angular distance L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 18/26
- 20. Intro ECA KECA Clustering Results Conclusions 1 Introduction 2 Entropy Component Analysis 3 Kernel Entropy Component Analysis (KECA) 4 KECA Spectral Clustering 5 Experimental Results 6 Conclusions and Open questions L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 19/26
- 21. Intro ECA KECA Clustering Results Conclusions Experimental results: Data material Cloud masking from ENVISAT/MERIS multispectral images Pixel-wise binary decisions about the presence/absence of clouds MERIS images taken over Spain and France Input samples with 13 spectral bands and 6 physically inspired features Barrax (BR-2003-07-14) Barrax (BR-2004-07-14) France (FR-2005-03-19) L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 20/26
- 22. Intro ECA KECA Clustering Results Conclusions Experimental results: Numerical comparison Experimental setup KECA compared with k-means, KPCA + k-means, and Kernel k-means Number of clusters fixed to k = 2 (cloud-free and cloudy areas) Number of KPCA and KECA features fixed to m = 2 (stress differences) RBF-kernel width parameter is selected by gird-search for all methods Numerical results Validation results on 10000 pixels per image manually labeled Kappa statistic results over 10 realizations for all images BR-2003-07-14 BR-2004-07-14 FR-2005-03-19 1 0.8 0.6 0.5 0.9 0.7 Estimated κ statistic Estimated κ statistic Estimated κ statistic 0.4 0.8 0.6 0.3 KECA 0.7 KPCA 0.2 Kernel k-means 0.5 k-means 0.6 0.1 0.5 0.4 0 200 400 600 800 1000 200 400 600 800 1000 200 400 600 800 1000 #Samples #Samples #Samples L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 21/26
- 23. Intro ECA KECA Clustering Results Conclusions Experimental results: Numerical comparison Average numerical results 0.8 0.7 Estimated κ statistic KECA 0.6 KPCA Kernel k-means k-means 0.5 0.4 200 400 600 800 1000 #Samples KECA outperforms k-means (+25%) and Kk-means and KPCA (+15%) In general, the number of training samples positively affect the results L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 22/26
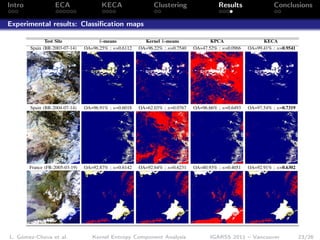
- 24. Intro ECA KECA Clustering Results Conclusions Experimental results: Classification maps Test Site k-means Kernel k-means KPCA KECA Spain (BR-2003-07-14) OA=96.25% ; κ=0.6112 OA=96.22% ; κ=0.7540 OA=47.52% ; κ=0.0966 OA=99.41% ; κ=0.9541 Spain (BR-2004-07-14) OA=96.91% ; κ=0.6018 OA=62.03% ; κ=0.0767 OA=96.66% ; κ=0.6493 OA=97.54% ; κ=0.7319 France (FR-2005-03-19) OA=92.87% ; κ=0.6142 OA=92.64% ; κ=0.6231 OA=80.93% ; κ=0.4051 OA=92.91% ; κ=0.6302 L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 23/26
- 25. Intro ECA KECA Clustering Results Conclusions 1 Introduction 2 Entropy Component Analysis 3 Kernel Entropy Component Analysis (KECA) 4 KECA Spectral Clustering 5 Experimental Results 6 Conclusions and Open questions L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 24/26
- 26. Intro ECA KECA Clustering Results Conclusions Conclusions and open questions Conclusions Kernel entropy component analysis for clustering remote sensing data Nonlinear features preserving entropy of the input data Angular clustering reveals structure in terms of clusters divergence Out-of-sample extension for test data → mandatory in remote sensing Good results on cloud screening from MERIS images KECA code is available at http://www.phys.uit.no/∼robertj/ Simple feature extraction toolbox (SIMFEAT) soon at http://isp.uv.es Open questions and Future work Pre-images of transformed data in the input space Learn kernel parameters in an automatic way Test KECA in more remote sensing applications L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 25/26
- 27. Intro ECA KECA Clustering Results Conclusions Kernel Entropy Component Analysis in Remote Sensing Data Clustering Luis Gómez-Chova1 Robert Jenssen2 Gustavo Camps-Valls1 1 Image Processing Laboratory (IPL), Universitat de València, Spain. [email protected] , http://www.valencia.edu/chovago 2 Department of Physics and Technology, University of Tromsø, Norway. [email protected] , http://www.phys.uit.no/∼robertj IGARSS 2011 – Vancouver, Canada * IPL Image Processing Laboratory L. Gómez-Chova et al. Kernel Entropy Component Analysis IGARSS 2011 – Vancouver 26/26