lecture 10 formal methods in software enginnering.pptx

1
Formal Methods in SE
Qaisar Javaid
Assistant Professor
Lecture # 10

2
A transition system
 A (finite) set of variables V over some
domain.
 A set of states S.
 A (finite) set of transitions T, each
transition e t has
 an enabling condition e, and
 a transformation t.
 An initial condition I.

3
Example
 V={a, b, c, d, e}.
 S: all assignments of natural numbers
for variables in V.
 T={c >0(c,e):=(c -1,e +1),
d >0(d,e):=(d -1,e +1)}
 I: c =a / d =b / e =0
 What does this transition system do?

4
The interleaving model
 An execution is a maximal finite or infinite
sequence of states s0, s1, s2, …
That is: finite if nothing is enabled from the last
state.
 The first state s0 satisfies the initial
condition, I.e., I (s0).
 Moving from one state si to its successor
si+1 is by executing a transition et:
 e (si), i.e., si satisfies e.
 si+1 is obtained by applying t to si.

5
Example:
 s0=<a=2, b=1, c=2, d=1, e=0>
 s1=<a=2, b=1, c=1, d=1, e=1>
 s2=<a=2, b=1, c=1, d=0, e=2>
 s3=<a=2, b=1 ,c=0, d=0, e=3>
T={c>0(c,e):=(c -1,e +1),
d>0(d,e):=(d-1,e+1)}
I: c=a / d=b / e=0

6
L0:While True do
NC0:wait(Turn=0);
CR0:Turn=1
endwhile ||
L1:While True do
NC1:wait(Turn=1);
CR1:Turn=0
endwhile
T0:PC0=L0PC0:=NC0
T1:PC0=NC0/Turn=0
PC0:=CR0
T2:PC0=CR0
(PC0,Turn):=(L0,1)
T3:PC1=L1PC1=NC1
PC1:=CR1
T5:PC1=CR1
(PC1,Turn):=(L1,0)
Initially: PC0=L0/PC1=L1
The transitions
Is this the only reasonable way to model this program?

7
The state graph:Successor relation
between reachable states.
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
NC0,L1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=0
CR0,L1
Turn=1
L0,CR1
Turn=1
NC0,CR1
Turn=1
L0,NC1
Turn=1
NC0,NC1
Turn=1
NC0,L1
Turn=1
L0,L1
T0 T0
T3 T3
T1 T4
T3
T0 T3
T0
T0 T4
T1 T3
T2
T2
T5
T5

8
Some important points
 Reachable states: obtained from an initial state
through a sequence of enabled transitions.
 Executions: the set of maximal paths (finite or
terminating in a node where nothing is
enabled).
 Nondeterministic choice: when more than a
single transition is enabled at a given state. We
have a nondeterministic choice when at least
one node at the state graph has more than one
successor.

9
Always ¬(PC0=CR0/PC1=CR1)
(Mutual exclusion)
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
NC0,L1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=0
CR0,L1
Turn=1
L0,CR1
Turn=1
NC0,CR1
Turn=1
L0,NC1
Turn=1
NC0,NC1
Turn=1
NC0,L1
Turn=1
L0,L1

10
Always if Turn=0 then at
some point Turn=1
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
NC0,L1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=0
CR0,L1
Turn=1
L0,CR1
Turn=1
NC0,CR1
Turn=1
L0,NC1
Turn=1
NC0,NC1
Turn=1
NC0,L1
Turn=1
L0,L1

11
Always if Turn=0 then at
some point Turn=1
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
NC0,L1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=0
CR0,L1
Turn=1
L0,CR1
Turn=1
NC0,CR1
Turn=1
L0,NC1
Turn=1
NC0,NC1
Turn=1
NC0,L1
Turn=1
L0,L1

12
Interleaving semantics:
Execute one transition at a time.
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=1
L0,CR1
Turn=1
L0,NC1
Need to check the property
for every possible interleaving!

13
Interleaving semantics
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=1
L0,CR1
Turn=1
L0,NC1
Turn=0
L0,L1
Turn=0
L0,NC1

14
L0:While True do
NC0:wait(Turn=0);
CR0:Turn=1
endwhile ||
L1:While True do
NC1:wait(Turn=1);
CR1:Turn=0
endwhile
T0:PC0=L0PC0:=NC0
T1:PC0=NC0/Turn=0PC0:=CR0
T1’:PC0=NC0/Turn=1PC0:=NC0
T2:PC0=CR0(PC0,Turn):=(L0,1)
T3:PC1==L1PC1=NC1
T4:PC1=NC1/Turn=1PC1:=CR1
T4’:PC1=NC1/Turn=0PC1:=NC1
T5:PC1=CR1(PC1,Turn):=(L1,0)
Busy waiting

15
Always when Turn=0 then
at some point Turn=1
Now it does not hold!
(Red subgraph generates a counterexample execution.)
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
NC0,L1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=0
CR0,L1
Turn=1
L0,CR1
Turn=1
NC0,CR1
Turn=1
L0,NC1
Turn=1
NC0,NC1
Turn=1
NC0,L1
Turn=1
L0,L1
T4’ T1’

16
Combinatorial explosion
V1:=1
V1:=3
V1:=2
Vn:=1
Vn:=3
Vn:=2
…
How many states?

17
Global states
3n states
v1=1,v2=1…vn=1
v1=2,v2=1…vn=1 v1=1,v2=1…vn=2
…
v1=3,v2=1…vn=1
…
…
v1=1,v2=1…vn=3

19
Properties of formalisms
 Formal. Unique interpretation.
 Intuitive. Simple to understand (visual).
 Succinct. Spec. of reasonable size.
 Effective.
 Check that there are no contradictions.
 Check that the spec. is implementable.
 Check that the implementation satisfies spec.
 Expressive.
 May be used to generate initial code.
Specifying the implementation or its properties?

20
A transition system
 A (finite) set of variables V.
 A set of states S.
 A (finite) set of transitions T, each transition et
has
 an enabling condition e and a transformation t.
 An initial condition I.
 Denote by R(s, s’) the fact that s’ is a successor of s.

21
The interleaving model
 An execution is a finite or infinite sequence of states s0, s1,
s2, …
 The initial state satisfies the initial condition, I.e., I (s0).
 Moving from one state si to si+1 is by executing a transition
et:
 e(si), I.e., si satisfies e.
 si+1 is obtained by applying t to si.
 Lets assume all sequences are infinite by extending finite
ones by “stuttering” the last state.

22
Temporal logic
 Dynamic, speaks about several “worlds”
and the relation between them.
 Our “worlds” are the states in an
execution.
 There is a linear relation between them,
each two sequences in our execution
are ordered.
 Interpretation: over an execution,
later over all executions.

23
LTL: Syntax
 ::= () | ¬ | /  / U
 |O  | p
“box”, “always”, “forever”
“diamond”, “eventually”, “sometimes”
O “nexttime”
U“until”
Propositions p, q, r, … Each represents some
state property (x>y+1, z=t, at_CR, etc.)

24
Semantics over suffixes of execution


O 
U


    









25
Can discard some operators
 Instead of <>p, write true U p.
 Instead of []p, we can write ¬(<>¬p),
or ¬(true U ¬p).
Because []p=¬¬[]p.
¬[]p means it is not true that p holds
forever, or at some point ¬p holds or
<>¬p.

26
Combinations
 []<>p “p will happen infinitely often”
 <>[]p “p will happen from some point
forever”.
 ([]<>p)  ([]<>q) “If p happens
infinitely often, then q also happens
infinitely often”.

27
Some relations:
 [](/)=([])/([])
 But <>(/)(<>)/(<>)
 <>(/)=(<>)/(<>)
 But [](/)([])/([])












28
What about
 ([]<>)/([]<>)=[]<>(/)?
 ([]<>)/([]<>)=[]<>(/)?
 (<>[])/(<>[])=<>[](/)?
 (<>[])/(<>[])=<>[](/)?
No, just 
Yes!!!
Yes!!!
No, just 

29
Formal semantic definition
 Let  be a sequence s0 s1 s2 …
 Let i be a suffix of : si si+1 si+2 … (0 = )
 i |= p, where p a proposition, if si|=p.
 i |= / if i |=  and i |= .
 i |= / if i |=  or i |= .
 i |= ¬ if it is not the case that i |= .
 i |= <> if for some ji, j |= .
 i |= [] if for each ji, j |= .
 i |= U  if for some ji, j|=.
and for each ik<j, k |=.

30
Then we interpret:
 For a state:
s|=p as in propositional logic.
 For an execution:
|= is interpreted over a sequence, as
in previous slide.
 For a system/program:
P|= holds if |= for every sequence
 of P.

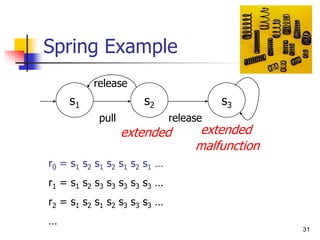
31
Spring Example
s1 s3
s2
pull
release
release
extended
malfunction
extended
r0 = s1 s2 s1 s2 s1 s2 s1 …
r1 = s1 s2 s3 s3 s3 s3 s3 …
r2 = s1 s2 s1 s2 s3 s3 s3 …
…

34
More specifications
 [] (PC0=NC0  <> PC0=CR0)
 [] (PC0=NC0 U Turn=0)
 Try at home:
- The processes alternate in entering
their critical sections.
- Each process enters its critical section
infinitely often.

35
Proof system
 ¬<>p<-->[]¬p
 [](pq)([]p[]q)
 []p(p/O[]p)
 O¬p<-->¬Op
 [](pOp)(p[]p)
 (pUq)<-->(q/(p/O(pUq)))
 (pUq)<>q
 + propositional logic
axiomatization.
 + proof rule:
_p_
[]p

36
Traffic light example
Green  Yellow  Red
Always has exactly one light:
[](¬(gr/ye)/¬(ye/re)/¬(re/gr)/(gr/ye/re))
Correct change of color:
[]((grU ye)/(yeU re)/(reU gr))

37
Another kind of traffic light
GreenYellowRedYellow
First attempt:
[](((gr/re) U ye)/(ye U (gr/re)))
Correct specification:
[]( (gr(gr U (ye / ( ye U re ))))
/(re(re U (ye / ( ye U gr ))))
/(ye(ye U (gr / re))))
Needed only when we
can start with yellow

38
Properties of sequential
programs
 init-when the program starts and
satisfies the initial condition.
 finish-when the program terminates and
nothing is enabled.
 Partial correctness: init/[](finish)
 Termination: init/<>finish
 Total correctness: init/<>(finish/ )
 Invariant: init/[]

39
Automata over finite words
 A=<S, S, , I, F>
 S (finite) - the alphabet.
 S (finite) - the states.
   S x S x S - the transition relation.
 I  S - the starting states.
 F  S - the accepting states.
a
a
b
b
s0 s1

40
The transition relation
 (s0, a, s0)
 (s0, b, s1)
 (s1, a, s0)
 (s1, b, s1)
a
a
b
b
s0 s1

41
A run over a word
 A word over S, e.g., abaab.
 A sequence of states, e.g. s0 s0 s1 s0 s0 s1.
 Starts with an initial state.
 Follows the transition relation (si, ci , si+1).
 Accepting if ends at accepting state.
a
a
b
b
s0 s1

42
The language of an
automaton
 The words that are accepted by the
automaton.
 Includes aabbba, abbbba.
 Does not include abab, abbb.
 What is the language?
a
a
b
b
s0 s1

43
Nondeterministic automaton
 Transitions: (s0,a ,s0), (s0,b ,s0),
(s0,a ,s1),(s1,a ,s1).
 What is the language of this
automaton?
a,b a
a
s0
s1

44
Equivalent deterministic automaton
b
a
a
s0 s1
b
a,b a
a
s0 s1

45
Automata over infinite words
 Similar definition.
 Runs on infinite words over S.
 Accepts when an accepting state occurs
infinitely often in a run.
a
a
b
b
s0 s1

46
Automata over infinite words
 Consider the word abababab…
 There is a run s0s0s1s0s1s0s1 …
 This run in accepting, since s0
appears infinitely many times.
a
a
b
b
s0 s1

47
Other runs
 For the word bbbbb… the run is
s0 s1 s1 s1 s1… and is not accepting.
 For the word aaabbbbb …, the
run is s0 s0 s0 s0 s1 s1 s1 s1 …
 What is the run for ababbabbb …?
a
a
b
b
s0 s1

48
Nondeterministic automaton
 What is the language of this automaton?
 What is the LTL specification if
b -- PC0=CR0, a =¬b?
•Can you find a deterministic automaton with same language?
•Can you prove there is no such deterministic automaton?
a,b
a
a
s0 s1

49
No deterministic automaton
for (a+b)*aω
 In a deterministic automaton there is one run for
each word.
 After some sequence of a’s, i.e., aaa…a must reach
some accepting state.
 Now add b, obtaining aaa…ab.
 After some more a’s, i.e., aaa…abaaa…a must reach
some accepting state.
 Now add b, obtaining aaa…abaaa…ab.
 Continuing this way, one obtains a run that has
infinitely many b’s but reaches an accepting state
(in a finite automaton, at least one would repeat)
infinitely often.

50
Specification using Automata
 Let each letter correspond to some propositional
property.
 Example: a -- P0 enters critical section,
b -- P0 does not enter section.
 []<>PC0=CR0
a
a
b
b
s0 s1

51
Mutual Exclusion
 a -- PC0=CR0/PC1=CR1
 b -- ¬(PC0=CR0/PC1=CR1)
 c -- true
 []¬(PC0=CR0/PC1=CR1)
b a c
s0 s1

52
L0:While True do
NC0:wait(Turn=0);
CR0:Turn=1
endwhile ||
L1:While True do
NC1:wait(Turn=1);
CR1:Turn=0
endwhile
T0:PC0=L0PC0=NC0
PC0:=CR0
T2:PC0=CR0
(PC0,Turn):=(L0,1)
T3:PC1==L1PC1=NC1
PC1:=CR1
T5:PC1=CR1
(PC1,Turn):=(L1,0)
Apply now to our
program:

53
The state space
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
NC0,L1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=0
CR0,L1
Turn=1
L0,CR1
Turn=1
NC0,CR1
Turn=1
L0,NC1
Turn=1
NC0,NC1
Turn=1
NC0,L1
Turn=1
L0,L1

54
[]¬(PC0=CR0/PC1=CR1)
(Mutual exclusion)
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
NC0,L1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=0
CR0,L1
Turn=1
L0,CR1
Turn=1
NC0,CR1
Turn=1
L0,NC1
Turn=1
NC0,NC1
Turn=1
NC0,L1
Turn=1
L0,L1

55
[](Turn=0 <>Turn=1)
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
NC0,L1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=0
CR0,L1
Turn=1
L0,CR1
Turn=1
NC0,CR1
Turn=1
L0,NC1
Turn=1
NC0,NC1
Turn=1
NC0,L1
Turn=1
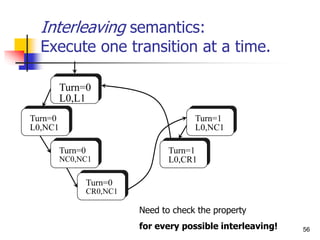
L0,L1

56
Interleaving semantics:
Execute one transition at a time.
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=1
L0,CR1
Turn=1
L0,NC1
Need to check the property
for every possible interleaving!

57
[](Turn=0  <>Turn=1)
Turn=0
L0,L1
Turn=0
L0,NC1
Turn=0
NC0,L1
Turn=0
CR0,NC1
Turn=0
NC0,NC1
Turn=0
CR0,L1
Turn=1
L0,CR1
Turn=1
NC0,CR1
Turn=1
L0,NC1
Turn=1
NC0,NC1
Turn=1
NC0,L1
Turn=1
L0,L1

58
Correctness condition
 We want to find a correctness condition
for a model to satisfy a specification.
 Language of a model: L(Model)
 Language of a specification: L(Spec).
 We need: L(Model)  L(Spec).

59
Correctness
All sequences
Sequences satisfying Spec
Program executions

60
Incorrectness
All sequences
Sequences satisfying Spec
Program executions
Counter
examples

61
Automatic Verification
(Book: Chapter 6)

62
How can we check the model?
 The model is a graph.
 The specification should refer the the
graph representation.
 Apply graph theory algorithms.

63
What properties can we check?
 Invariant: a property that needs to
hold in each state.
 Deadlock detection: can we reach a
state where the program is blocked?
 Dead code: does the program have
parts that are never executed.

lecture 10 formal methods in software enginnering.pptx

More Related Content

Similar to lecture 10 formal methods in software enginnering.pptx (20)

Recently uploaded (20)

lecture 10 formal methods in software enginnering.pptx