lecture 1(Fundamental of algorithms).pptx

Copyright © 2007 Pearson Addison-Wesley. All rights reserved. A. Levitin “Introduction to the Design & Analysis of Algorithms,” 2nd ed., Ch. 1
CSE408
Fundamentals of Algorithms
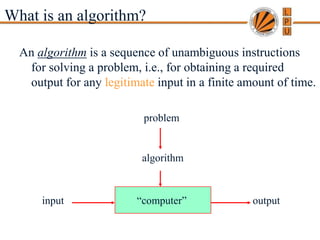
Lecture #1

What is an algorithm?
An algorithm is a sequence of unambiguous instructions
for solving a problem, i.e., for obtaining a required
output for any legitimate input in a finite amount of time.
“computer”
problem
algorithm
input output

Algorithm
 An algorithm is a sequence of unambiguous
instructions for solving a problem, i.e., for obtaining a
required output for any legitimate input in a finite
amount of time.
• Can be represented various forms
• Unambiguity/clearness
• Effectiveness
• Finiteness/termination
• Correctness

Historical Perspective
 Euclid’s algorithm for finding the greatest common divisor
 Muhammad ibn Musa al-Khwarizmi – 9th century
mathematician
www.lib.virginia.edu/science/parshall/khwariz.html

Notion of algorithm and problem
“computer”
algorithmic solution
(different from a conventional solution)
problem
algorithm
input
(or instance)
output

Example of computational problem: sorting
 Statement of problem:
• Input: A sequence of n numbers <a1, a2, …, an>
• Output: A reordering of the input sequence <a´
1, a´
2, …, a´
n> so that a´
i
≤ a´
j whenever i < j
 Instance: The sequence <5, 3, 2, 8, 3>
 Algorithms:
• Selection sort
• Insertion sort
• Merge sort
• (many others)

Selection Sort
 Input: array a[1],…,a[n]
 Output: array a sorted in non-decreasing order
 Algorithm:
for i=1 to n
swap a[i] with smallest of a[i],…,a[n]
• Is this unambiguous? Effective?
• See also pseudocode, section 3.1

Some Well-known Computational Problems
 Sorting
 Searching
 Shortest paths in a graph
 Minimum spanning tree
 Primality testing
 Traveling salesman problem
 Knapsack problem
 Chess
 Towers of Hanoi
 Program termination
Some of these problems don’t have efficient algorithms,
or algorithms at all!

Basic Issues Related to Algorithms
 How to design algorithms
 How to express algorithms
 Proving correctness
 Efficiency (or complexity) analysis
• Theoretical analysis
• Empirical analysis
 Optimality

Algorithm design strategies
 Brute force
 Divide and conquer
 Decrease and conquer
 Transform and conquer
 Greedy approach
 Dynamic programming
 Backtracking and branch-and-bound
 Space and time tradeoffs

Analysis of Algorithms
 How good is the algorithm?
• Correctness
• Time efficiency
• Space efficiency
 Does there exist a better algorithm?
• Lower bounds
• Optimality

What is an algorithm?
 Recipe, process, method, technique, procedure, routine,…
with the following requirements:
1. Finiteness
 terminates after a finite number of steps
2. Definiteness
 rigorously and unambiguously specified
3. Clearly specified input
 valid inputs are clearly specified
4. Clearly specified/expected output
 can be proved to produce the correct output given a valid input
5. Effectiveness
 steps are sufficiently simple and basic

Why study algorithms?
 Theoretical importance
• the core of computer science
 Practical importance
• A practitioner’s toolkit of known algorithms
• Framework for designing and analyzing algorithms for new problems
Example: Google’s PageRank Technology

Euclid’s Algorithm
Problem: Find gcd(m,n), the greatest common divisor of two
nonnegative, not both zero integers m and n
Examples: gcd(60,24) = 12, gcd(60,0) = 60, gcd(0,0) = ?
Euclid’s algorithm is based on repeated application of equality
gcd(m,n) = gcd(n, m mod n)
until the second number becomes 0, which makes the problem
trivial.
Example: gcd(60,24) = gcd(24,12) = gcd(12,0) = 12

Two descriptions of Euclid’s algorithm
Step 1 If n = 0, return m and stop; otherwise go to Step 2
Step 2 Divide m by n and assign the value of the remainder to r
Step 3 Assign the value of n to m and the value of r to n. Go to
Step 1.
while n ≠ 0 do
r ← m mod n
m← n
n ← r
return m

Fundamentals of Algorithmic Problem Solving

Two main issues related to algorithms
 How to design algorithms
 How to analyze algorithm efficiency

Algorithm design techniques/strategies
 Brute force
 Divide and conquer
 Decrease and conquer
 Transform and conquer
 Space and time tradeoffs
 Greedy approach
 Dynamic programming
 Iterative improvement
 Backtracking
 Branch and bound

Analysis of algorithms
 How good is the algorithm?
• time efficiency
• space efficiency
• correctness ignored in this course
 Does there exist a better algorithm?
• lower bounds
• optimality

Important problem types
 sorting
 searching
 string processing
 graph problems
 combinatorial problems
 geometric problems
 numerical problems

Sorting (I)
 Rearrange the items of a given list in ascending order.
• Input: A sequence of n numbers <a1, a2, …, an>
• Output: A reordering <a´
1, a´
2, …, a´
n> of the input sequence such that a´
1≤
a´
2 ≤ … ≤ a´
n.
 Why sorting?
• Help searching
• Algorithms often use sorting as a key subroutine.
 Sorting key
• A specially chosen piece of information used to guide sorting. E.g., sort
student records by names.

Sorting (II)
 Examples of sorting algorithms
• Selection sort
• Bubble sort
• Insertion sort
• Merge sort
• Heap sort …
 Evaluate sorting algorithm complexity: the number of key comparisons.
 Two properties
• Stability: A sorting algorithm is called stable if it preserves the relative order of any
two equal elements in its input.
• In place : A sorting algorithm is in place if it does not require extra memory,
except, possibly for a few memory units.

Selection Sort
Algorithm SelectionSort(A[0..n-1])
//The algorithm sorts a given array by selection sort
//Input: An array A[0..n-1] of orderable elements
//Output: Array A[0..n-1] sorted in ascending order
for i  0 to n – 2 do
min  i
for j  i + 1 to n – 1 do
if A[j] < A[min]
min  j
swap A[i] and A[min]

Searching
 Find a given value, called a search key, in a given set.
 Examples of searching algorithms
• Sequential search
• Binary search …
Input: sorted array a_i < … < a_j and key x;
m (i+j)/2;
while i < j and x != a_m do
if x < a_m then j  m-1
else i  m+1;
if x = a_m then output a_m;
Time: O(log n)

String Processing
 A string is a sequence of characters from an alphabet.
 Text strings: letters, numbers, and special characters.
 String matching: searching for a given word/pattern in a text.
Examples:
(i) searching for a word or phrase on WWW or in a
Word document
(ii) searching for a short read in the reference genomic
sequence

lecture 1(Fundamental of algorithms).pptx

More Related Content

Similar to lecture 1(Fundamental of algorithms).pptx (20)

Recently uploaded (20)

lecture 1(Fundamental of algorithms).pptx