Lecture 4 errors detection
- 1. Lecture 4 Error control. (2 hours) 01/01/04 1
- 2. Contents • Principle of error control • Detections • Corrections • Error detection algorithms – Single Parity – 2 Dimensional Parity – 1st compliment sum – Check sum 01/01/04 2
- 3. Coding and Error Control • Despite the modulation techniques used, it is possible that the data send through a medium is corrupted, by one of the distortion sources we discussed earlier. To recover from errors, network protocols provide mechanisms, usually implemented at the transport or data link layer in the ISO–model. • Error Detections: the protocol simply detects the occurrences of errors and requires then a retransmission using the time out or a negative acknowledgement. • Error Correction (Forward Error Correction FEC) are complex and costly algorithms that correct some of the errors reported in the transmission. • Although is subject is very complex and outside the scope of this course, we will highlight some basic principles for error detections and corrections 01/01/04 3
- 4. Recall!!! Binary addition: 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 Eg: 1001 + 1111 ----------- 11000 sum --------- 1111 carry Binary inverse: Inverse of 0 is 1 Inverse of 1 is 0 Eg: 100101101 011010010 Modulo-2 / XOR operation 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 Eg: 1001 1111 ----------- 0110 01/01/04 4
- 5. Parity checks (1) • Single parity: This scheme is simple and inexpensive. It can only be used for short communication, such as PC to a printer connections. It can only detects single errors, or an even or an odd number of errors (depending on the type of the parity). For instance, for an even parity check, an additional parity bit is used to report the number of even 1s in the signal. If the number of 1s is even the parity bit is set to 0. Obviously, an odd number of 1s will be detected. • Two-dimensional parity: In this scheme data is organised as a matrix and single parities are applied to columns and rows. With this approach, some errors can be corrected, in addition to detection. – Single errors can be detected and corrected – Double errors can be detected, but not necessarily corrected. – Triple Errors can not be necessarily detected and corrected 01/01/04 5
- 6. 01111011 Sender 01111011 0 Single dimensional Parity, example 01110011 0 Receiver 01110011 0 1 Single Error Detected 01/01/04 6
- 7. Two dimensional Parity, example 0111000110101011 Sender 0 1 1 1 1 0 0 0 1 1 1 0 1 0 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 0 0 1 1 1 1 0 1 0 0 1 0 1 1 1 0 1 1 1 1 Receiver 0 1 1 1 1 0 0 0 1 1 1 1 1 0 1 0 0 0 1 0 1 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 01/01/04 7
- 8. Two dimensional Parity, example 0111000110101011 Sender 0 1 1 1 1 0 0 0 1 1 1 0 1 0 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 0 0 1 1 1 1 1 1 0 0 1 0 1 1 1 0 1 1 1 1 Receiver 0 1 1 1 1 0 0 0 1 1 1 1 1 1 1 0 0 1 1 0 1 1 1 0 0 1 1 1 1 0 0 1 1 0 0 0 Detect two errors, but cannot correct 01/01/04 8
- 9. Two dimensional Parity, example 0111000110101011 Sender 0 1 1 1 1 0 0 0 1 1 1 0 1 0 0 1 0 1 1 1 0 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 0 1 1 1 0 1 1 1 1 Receiver 0 1 1 1 1 0 0 1 1 1 1 0 1 1 1 0 0 1 1 0 1 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 Cannot detect 3 errors 01/01/04 9
- 10. Check-summing methods (1) • These techniques involve performing some arithmetic operation on the m-bit message to produce the r-bit check sum. The receiver applied the same operation on the check sum and the original message to detect error. • 1’s compliment check sum (Internet Check Sum): Mainly used in the TCP/UDP protocols for it simplicity. • Message is divided into r-fields all fields are added together and the final sum is inverted. The same operation is applied at the receiver, where the new check sum is added to the received one, the result should be all 111111111, otherwise an error has occurred. A A 1 • The principle of the Arithmetic addition 01/01/04 10
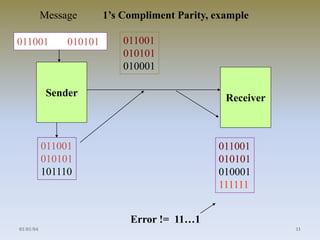
- 11. Message 1’s Compliment Parity, example 011001 010101 Sender 011001 010101 101110 011001 010101 010001 Receiver 011001 010101 010001 111111 Error != 11…1 01/01/04 11
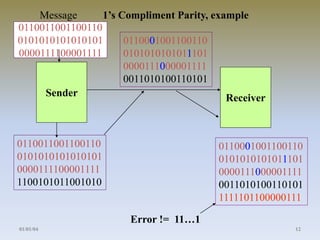
- 12. Message 1’s Compliment Parity, example 0110011001100110 0101010101010101 0000111100001111 Sender 0110011001100110 0101010101010101 0000111100001111 1100101011001010 0110001001100110 0101010101011101 0000111000001111 0011010100110101 Receiver 0110001001100110 0101010101011101 0000111000001111 0011010100110101 1111101100000111 Error != 11…1 01/01/04 12
- 13. Check-summing methods (2) • The most popular coding technique used in Ethernet, MAC layer is the cyclic redundancy check code (CRC) also known as the polynomial code. A generator code is used to divide the message, modulo 2 division, then the remainder of the division is used as the check sum. • The sender calculates r = m%g, using XOR operation, where m is the message, g is the polynomial, of degree n (the number of bits +1) and r is the reminder. It sends (m+r). • The receiver computes (m+r)%g = 0, no errors, otherwise errors have occurred. • The generator are specially chosen, for instance IEEE802 is a 32 bit code. 01/01/04 13
- 14. Check-summing methods (3) • It can be proven that the CRC scheme 1. Detect single and double errors. 2. Detect all odd number of errors. 3. Detect all burst errors <= than the number of bits +1 in the generator, n, (IEEE802, burst less 32 are detected) 4. Furthermore, the probability that a burst error greater than n is not detected is 2-n . For generator of 32 bits, this probability that an error is not detected is 2-31. 01/01/04 14
- 15. Example Message m = 1101011011, Generator g = 10011 degree n=4. r = m%g as follows. 10011 11010110110000 10011 010011 10011 0000010110 10011 0010100 10011 001110 Thus r = 1110, and the full packet will be 1101011011 1110 01/01/04 15
- 16. Animated Example 10011 110101101100 0 0 10011 010011 10011 0000010110 10011 00101 00 10011 00111 0 01/01/04 16
- 17. At the receiver, the remainder is zero, there are no errors. 11010110111110 10011 010011 10011 0000010111 10011 0010011 10011 000000 At the receiver, the remainder is not zero, there are errors. 10110100111110 10011 0010110 10011 0010101 10011 0011011 10011 010001 10011 0001010 01/01/04 17
- 18. Quiz – What happen when an error is detected by the sender? Discuss two possibilities. – How many errors can be corrected with 2Dimensional parity bits? – What is the chance of not detecting an error with a generator of 32-bits, in checksum algorithm? 01/01/04 18