Drawing Tools
- 1. A Lecture by Abdul Ghaffar on Drawing Tools Reference Chapter #3 of text book
- 2. World, Windows, Viewports World Coordinates are the usual certain xy-coordinates used in mathematics based on whatever units are convenient. World window specifies which rectangle part of world should be drawn, and which clipped away. Viewport defined in screen window mapping (scaling, shifting) between world window and viewport draw in world window; automatically mapped to viewport
- 3. 3.2.1 Window to viewport mapping World window and viewport
- 4. 3.2.1 Window to viewport mapping Borders of world window as left, top, right, bottom Likewise Viewport is described within the coordinate system of the screen measured in pixel.
- 5. 3.2.1 Window to viewport mapping World window can be of any size and shape Viewport can be of any size within the screen coordinate WW and VP may have different aspect ratios, which will cause distortion in the picture.
- 6. 3.2.1 Window to viewport mapping Window to viewport mapping If x is 40% of the way over from the left edge of the window then sx is 40% of the way over from the left edge of the viewport If y is some fraction f of the height of the window from the bottom, sy must be the same fraction f up from the bottom of the viewport. This proportionality forces the mapping to have the linear form sx = Ax + C sy = Bx + D The only task is to calculate the four constant A, B, C, D
- 7. 3.2.1 Window to viewport mapping From figure and similarly (x,y) W.t W.b W.l W.r (sx,sy) V.t V.b V.l V.r W V x sx y sy
- 8. Derivation for sx: Repeat same process for sy
- 9. 3.2.1 Window to viewport mapping After repeating same process for sy finally we get
- 10. Doing it in OpenGL void glOrtho2D (GLdouble left, GLdouble right, GLdouble bottom, GLdouble top) void glViewport (GLlint x, GLlint y, GLlint Width, GLlint Height)
- 11. Example:
- 12. 3.2.2 Setting the window and viewport automatically Find the extant
- 13. 3.2.2 Setting the window and viewport automatically Find the aspect ratio R If R > W / H then setViewport (0, W, 0, W / R); If R < W / H then setViewport ( 0. H * R, 0, H );
- 14. Self study and exercises: Example 3.2.1 , window and viewport exercise 3.2.1 , building the mapping example 3.2.2 , plotting sine function Ex. 3.2.3 Drawing polylines from a file Ex. 3.2.4 Tiling a window with a motif Ex. 3.2.5 Clipping, zooming and roaming Ex. 3.2.7 A tall window Ex 3.2.8 A short window
- 15. Chapter 3: Windows, viewports 3.3 Clipping lines Some possible situations Entire line lies within the window (trivial accept) Entire line lies outside the window (trivial reject) One point is inside and one is outside Both points are outside of the window and a segment lies inside the window.
- 16. Chapter 3: Windows, viewports 3.3.2 Cohen-Sutherland clipping Checks for trivial accept or trivial reject Construct Inside-outside code word for each endpoint Trivial accept: Both code words are FFFF Trivial reject: Code words have T in same position
- 17. 3.3.2 Cohen-Sutherland clipping Algorithm do { form the code word for p1 and p2 if ( trivial accept ) return 1; if ( trivial reject ) return 0; chop the line at the “next” window border; discard the “outside” part; } while (1);
- 18. 3.3.2 Cohen-Sutherland clipping Chopping (no trivial accept/reject) Example: if a point is to the right of the window Goal : Calculate the location of point A I.e A.x and A.y A.x = W.right A.y ? A.y = p1.y + d d = ? From figure e = W.right – P 1 .x delx = P 2 .x – P 1 .x dely = P 2 .y – P 1 .y To find d we set a relation as Therefore new P1 is p1,x = W.right p1.y = p1.y + d
- 19. 3.3.2 Cohen-Sutherland clipping Similarly if the point is to the left of the window then e = W.left – P 1 .x and d = e * m p1.x = W.left and p1.y = p1.y + d if the point is below the bottom of the window then e = W.bottom – P 1 .y and d = e / m p1.y = W.bottom and p1.x = p1.y + d if the point is below the top of the window then e = W.top – P 1 .y and d = e / m p1.y = W.top and p1.x = p1.y + d
- 20. 3.3.2 Cohen-Sutherland clipping Example : A segment that requires four clips
- 21. 3.3.2 Cohen-Sutherland clipping (Complete Algorithm:)
- 22. Chapter 3: Windows, viewports The Canvas Class: Self study. 3.4 Developing the canvas class Page 101 Structures , Point2 and Rect Page 102 Canvas class declaration Page 103 class constructor Page 104 MoveTo, LineTo, setwndow Page 105 Move and line relative Page 107 turnto, turn, forward
- 23. Chapter 3: Windows, viewports Page 106 Example 3.5.3 Polyspiral for ( …..) { forward(length, 1); turn(angle); length+=increment) }
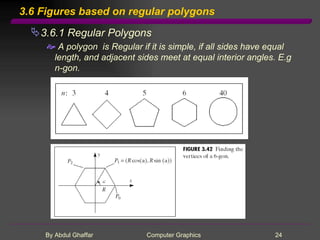
- 24. 3.6 Figures based on regular polygons 3.6.1 Regular Polygons A polygon is Regular if it is simple, if all sides have equal length, and adjacent sides meet at equal interior angles. E.g n-gon.
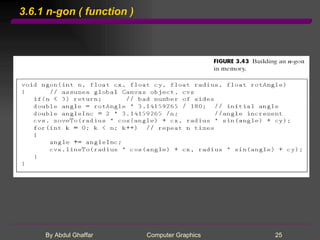
- 25. 3.6.1 n-gon ( function )
- 26. 3.6 Figures based on regular polygons Example 3.6.2 rosette (p.112) 3.7 Drawing circles and arcs
- 28. Chapter 3: Windows, viewports 3.8 Parametric forms of curves Implicit : Point on line if F(x,y) = 0 Line f ( x, y ) = ( y – y1 ) ( x2 - x1 ) - ( x - x1 ) ( y2 - y1 ) Circle f ( x, y ) = x 2 + y 2 –R 2 Parametric: Position at time t is given by x(t), y(t) Line x ( t ) = A x + ( B x – A x ) t y ( t ) = A y + ( B y – A y ) t Ellipse x ( t ) = W cos( t ) y ( t ) = H sine( t ) Circle x ( t ) = R cos( t ) y ( t ) = R sine( t )
- 29. Chapter 3: Windows, viewports Drawing parametric curves:
- 30. Chapter 3: Windows, viewports 3.8.3 Super-ellipses Implicit : (x/W) n + (y/H) n =1 Parametric: x(t) = W cos(t) |cos(t) 2/n-1 | y(t) = H sin(t) |sin(t) 2/n-1 | Super Ellipse: n=1 -> Square n<1 -a Inward n>1 -> outward
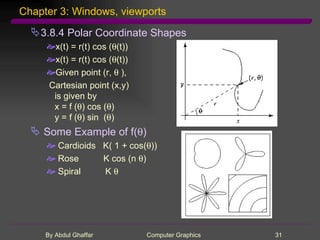
- 31. Chapter 3: Windows, viewports 3.8.4 Polar Coordinate Shapes x(t) = r(t) cos ( (t)) x(t) = r(t) cos ( (t)) Given point (r, ), Cartesian point (x,y) is given by x = f ( ) cos ( ) y = f ( ) sin ( ) Some Example of f( ) Cardioids K( 1 + cos( )) Rose K cos (n ) Spiral K