Lecture21
- 1. Physics 101: Lecture 21 Waves Today’s lecture will cover Textbook Chapter 11 Exam III
- 2. Preflight 5 Which concepts did you find the most difficult when preparing for this lecture? Standing waves was difficult to understand. What does it mean and can you give another explanation as to how to calculate it? Also, reflection was not explained enough. What is the difference between a fixed and a free boundary? Everything… Nothing… Overtones! harmonic waves. Longitudinal waves. there was alot of info Not paying attention
- 3. Waves Overview Types Speed Harmonic Superposition Standing
- 4. Types of Waves 8 Longitudinal: The medium oscillates in the same direction as the wave is moving Sound Slinky demo Transverse: The medium oscillates perpendicular to the direction the wave is moving. Water (more or less) Slinky demo
- 5. Slinky Preflight 3 Suppose that a longitudinal wave moves along a Slinky at a speed of 5 m/s. Does one coil of the slinky move through a distance of five meters in one second? 1. Yes 2. No the coil won't move, 5m/s is the speed for wave propagation 12 correct 5m
- 6. Velocity of Waves Act 17 A spring and slinky are attached and stretched. Compare the speed of the wave pulse in the slinky with the speed of the wave pulse in the spring. A) v slinky > v spring B) v slinky = v spring C) v slinky < v spring Slinky stretches more, so it has a smaller mass/length
- 7. Harmonic Waves Wavelength: The distance between identical points on the wave. Amplitude: The maximum displacement A of a point on the wave. 20 y(x,t) = A cos( t –kx) Angular Frequency : = 2 f x y Wave Number k: k = 2 / Recall: f = v / “ the weird/new symbols get me confused i never know what they represent “ Wavelength Amplitude A A
- 8. Period and Velocity 22 Period: The time T for a point on the wave to undergo one complete oscillation. Speed: The wave moves one wavelength in one period T so its speed is v = / T .
- 9. Harmonic Waves Exercise y(x,t) = A cos( t –kx) Label axis and tic marks if the graph shows a snapshot of the wave y(x,t) = 2 cos(4t –2x) at x=0. Recall: T = 2 / T = 2 25 t +2 -2 / 2 /4 /4
- 10. Preflight 1+2 Suppose a periodic wave moves through some medium. If the period of the wave is increased, what happens to the wavelength of the wave assuming the speed of the wave remains the same? 1. The wavelength increases 2. The wavelength remains the same 3. The wavelength decreases v = λ/ T 26 correct
- 11. ACT The wavelength of microwaves generated by a microwave oven is about 3 cm . At what frequency do these waves cause the water molecules in your burrito to vibrate ? (a) 1 GHz (b) 10 GHz (c) 100 GHz 1 GHz = 10 9 cycles/sec The speed of light is c = 3x10 8 m/s 29
- 12. ACT Solution Recall that v = f . 1 GHz = 10 9 cycles/sec The speed of light is c = 3x10 8 m/s 30 H H O Makes water molecules wiggle
- 13. Absorption coefficient of water as a function of frequency. 31 f = 10 GHz Visible “ water hole”
- 14. Interference and Superposition When two waves overlap, the amplitudes add. Constructive: increases amplitude Destructive : decreases amplitude 34
- 15. Reflection Act A slinky is connected to a wall at one end. A pulse travels to the right, hits the wall and is reflected back to the left. The reflected wave is A) Inverted B) Upright Fixed boundary reflected wave inverted Free boundary reflected wave upright 37
- 16. Standing Waves Fixed Endpoints Fundamental n=1 (2 nodes) n = 2L/n f n = n v / (2L) 44
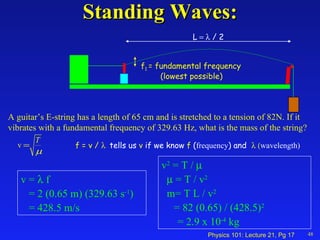
- 17. Standing Waves: 48 A guitar’s E-string has a length of 65 cm and is stretched to a tension of 82N. If it vibrates with a fundamental frequency of 329.63 Hz, what is the mass of the string? v = f = 2 (0.65 m) (329.63 s -1 ) = 428.5 m/s v 2 = T / = T / v 2 m= T L / v 2 = 82 (0.65) / (428.5) 2 = 2.9 x 10 -4 kg f 1 = fundamental frequency (lowest possible) L / 2 f = v / tells us v if we know f ( frequency ) and wavelength)
- 18. Summary Wave Types Transverse (eg pulse on string, water) Longitudinal (sound, slinky) Harmonic y(x,t) = A cos( t –kx) or A sin( t – kx) Superposition Just add amplitudes Reflection (fixed point inverts wave) Standing Waves (fixed ends) n = 2L/n f n = n v / 2L 50
Editor's Notes
- #2: 1
- #5: Stadium wave here, for fun.
- #7: Long Spring and slinky equal length (8 feet each) speeds up a LOT in slinky because mu is small and T is same.
- #8: Add stuff here
- #10: Students make plot at x=0, give them line, they mark tics
- #15: Do this with springs
- #16: Use large spring as demo here
- #17: Two people with large spring, can produce all of these as demo.
- #18: Calculate tension in guitar string given mass density and frequency. Ch 11 # 45