Lesson 25: Evaluating Definite Integrals (slides)
- 1. Sec on 5.3 Evalua ng Definite Integrals V63.0121.011: Calculus I Professor Ma hew Leingang New York University April 27, 2011 .
- 2. Announcements Today: 5.3 Thursday/Friday: Quiz on 4.1–4.4 Monday 5/2: 5.4 Wednesday 5/4: 5.5 Monday 5/9: Review and Movie Day! Thursday 5/12: Final Exam, 2:00–3:50pm
- 3. Objectives Use the Evalua on Theorem to evaluate definite integrals. Write an deriva ves as indefinite integrals. Interpret definite integrals as “net change” of a func on over an interval.
- 4. Outline Last me: The Definite Integral The definite integral as a limit Proper es of the integral Evalua ng Definite Integrals Examples The Integral as Net Change Indefinite Integrals My first table of integrals Compu ng Area with integrals
- 5. The definite integral as a limit Defini on If f is a func on defined on [a, b], the definite integral of f from a to b is the number ∫ b ∑n f(x) dx = lim f(ci ) ∆x a n→∞ i=1 b−a where ∆x = , and for each i, xi = a + i∆x, and ci is a point in n [xi−1 , xi ].
- 6. The definite integral as a limit Theorem If f is con nuous on [a, b] or if f has only finitely many jump discon nui es, then f is integrable on [a, b]; that is, the definite ∫ b integral f(x) dx exists and is the same for any choice of ci . a
- 7. Notation/Terminology ∫ b f(x) dx a ∫ — integral sign (swoopy S) f(x) — integrand a and b — limits of integra on (a is the lower limit and b the upper limit) dx — ??? (a parenthesis? an infinitesimal? a variable?) The process of compu ng an integral is called integra on
- 8. Example ∫ 1 4 Es mate dx using M4 . 0 1 + x2
- 9. Example ∫ 1 4 Es mate dx using M4 . 0 1 + x2 Solu on 1 1 3 We have x0 = 0, x1 = , x2 = , x3 = , x4 = 1. 4 2 4 1 3 5 7 So c1 = , c2 = , c3 = , c4 = . 8 8 8 8
- 10. Example ∫ 1 4 Es mate dx using M4 . 0 1 + x2 Solu on ( ) 1 4 4 4 4 M4 = 2 + 2 + 2 + 4 1 + (1/8) 1 + (3/8) 1 + (5/8) 1 + (7/8)2
- 11. Example ∫ 1 4 Es mate dx using M4 . 0 1 + x2 Solu on ( ) 1 4 4 4 4 M4 = + + + 4 1 + (1/8)2 1 + (3/8)2 1 + (5/8)2 1 + (7/8)2 ( ) 1 4 4 4 4 = + + + 4 65/64 73/64 89/64 113/64
- 12. Example ∫ 1 4 Es mate dx using M4 . 0 1 + x2 Solu on ( ) 1 4 4 4 4 M4 = + + + 4 1 + (1/8)2 1 + (3/8)2 1 + (5/8)2 1 + (7/8)2 ( ) 1 4 4 4 4 = + + + 4 65/64 73/64 89/64 113/64 64 64 64 64 = + + + ≈ 3.1468 65 73 89 113
- 13. Properties of the integral Theorem (Addi ve Proper es of the Integral) Let f and g be integrable func ons on [a, b] and c a constant. Then ∫ b 1. c dx = c(b − a) a ∫ b ∫ b ∫ b 2. [f(x) + g(x)] dx = f(x) dx + g(x) dx. a a a ∫ b ∫ b 3. cf(x) dx = c f(x) dx. ∫a b a ∫ b ∫ b 4. [f(x) − g(x)] dx = f(x) dx − g(x) dx. a a a
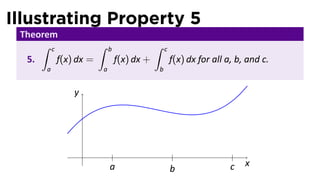
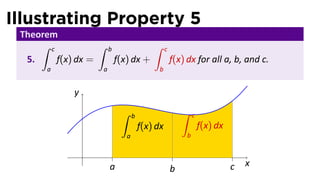
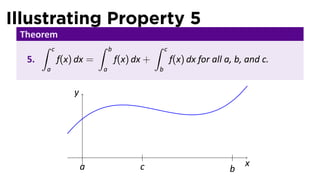
- 14. More Properties of the Integral Conven ons: ∫ ∫ a b f(x) dx = − f(x) dx b a ∫ a f(x) dx = 0 a This allows us to have Theorem ∫ c ∫ b ∫ c 5. f(x) dx = f(x) dx + f(x) dx for all a, b, and c. a a b
- 15. Illustrating Property 5 Theorem ∫ c ∫ b ∫ c 5. f(x) dx = f(x) dx + f(x) dx for all a, b, and c. a a b y . a c x b
- 16. Illustrating Property 5 Theorem ∫ c ∫ b ∫ c 5. f(x) dx = f(x) dx + f(x) dx for all a, b, and c. a a b y ∫ b f(x) dx a . a c x b
- 17. Illustrating Property 5 Theorem ∫ c ∫ b ∫ c 5. f(x) dx = f(x) dx + f(x) dx for all a, b, and c. a a b y ∫ b ∫ c f(x) dx f(x) dx a b . a c x b
- 18. Illustrating Property 5 Theorem ∫ c ∫ b ∫ c 5. f(x) dx = f(x) dx + f(x) dx for all a, b, and c. a a b y ∫ b ∫ c ∫ c f(x) dx f(x) dx f(x) dx a a b . a c x b
- 19. Illustrating Property 5 Theorem ∫ c ∫ b ∫ c 5. f(x) dx = f(x) dx + f(x) dx for all a, b, and c. a a b y . a c x b
- 20. Illustrating Property 5 Theorem ∫ c ∫ b ∫ c 5. f(x) dx = f(x) dx + f(x) dx for all a, b, and c. a a b y ∫ b f(x) dx a . a c x b
- 21. Illustrating Property 5 Theorem ∫ c ∫ b ∫ c 5. f(x) dx = f(x) dx + f(x) dx for all a, b, and c. a a b y ∫ c f(x) dx = b∫ b − f(x) dx . c a c x b
- 22. Illustrating Property 5 Theorem ∫ c ∫ b ∫ c 5. f(x) dx = f(x) dx + f(x) dx for all a, b, and c. a a b y ∫ ∫ c c f(x) dx f(x) dx = b∫ a b − f(x) dx . c a c x b
- 23. Definite Integrals We Know So Far If the integral computes an area and we know the area, we can use that. For instance, ∫ 1√ y π 1 − x2 dx = 0 4 By brute force we computed . ∫ 1 ∫ 1 x 2 1 1 x dx = x3 dx = 0 3 0 4
- 24. Comparison Properties of the Integral Theorem Let f and g be integrable func ons on [a, b].
- 25. Comparison Properties of the Integral Theorem Let f and g be integrable func ons on [a, b]. ∫ b 6. If f(x) ≥ 0 for all x in [a, b], then f(x) dx ≥ 0 a
- 26. Comparison Properties of the Integral Theorem Let f and g be integrable func ons on [a, b]. ∫ b 6. If f(x) ≥ 0 for all x in [a, b], then f(x) dx ≥ 0 a ∫ b ∫ b 7. If f(x) ≥ g(x) for all x in [a, b], then f(x) dx ≥ g(x) dx a a
- 27. Comparison Properties of the Integral Theorem Let f and g be integrable func ons on [a, b]. ∫ b 6. If f(x) ≥ 0 for all x in [a, b], then f(x) dx ≥ 0 a ∫ b ∫ b 7. If f(x) ≥ g(x) for all x in [a, b], then f(x) dx ≥ g(x) dx a a 8. If m ≤ f(x) ≤ M for all x in [a, b], then ∫ b m(b − a) ≤ f(x) dx ≤ M(b − a) a
- 28. Integral of a nonnegative function is nonnegative Proof. If f(x) ≥ 0 for all x in [a, b], then for any number of divisions n and choice of sample points {ci }: ∑ n ∑ n Sn = f(ci ) ∆x ≥ 0 · ∆x = 0 i=1 ≥0 i=1 . x Since Sn ≥ 0 for all n, the limit of {Sn } is nonnega ve, too: ∫ b f(x) dx = lim Sn ≥ 0 a n→∞ ≥0
- 29. The integral is “increasing” Proof. Let h(x) = f(x) − g(x). If f(x) ≥ g(x) for all x in [a, b], then h(x) ≥ 0 for all f(x) x in [a, b]. So by the previous h(x) g(x) property ∫ b h(x) dx ≥ 0 . x a This means that ∫ b ∫ b ∫ b ∫ b f(x) dx − g(x) dx = (f(x) − g(x)) dx = h(x) dx ≥ 0 a a a a
- 30. Bounding the integral Proof. If m ≤ f(x) ≤ M on for all x in [a, b], then by y the previous property ∫ b ∫ b ∫ b M m dx ≤ f(x) dx ≤ M dx a a a f(x) By Property 8, the integral of a constant func on is the product of the constant and m the width of the interval. So: ∫ b . x m(b − a) ≤ f(x) dx ≤ M(b − a) a b a
- 31. Example ∫ 2 1 Es mate dx using the comparison proper es. 1 x
- 32. Example ∫ 2 1 Es mate dx using the comparison proper es. 1 x Solu on Since 1 1 1 ≤ ≤ 2 x 1 for all x in [1, 2], we have ∫ 2 1 1 ·1≤ dx ≤ 1 · 1 2 1 x
- 33. Ques on ∫ 2 1 Es mate dx with L2 and R2 . Are your es mates overes mates? 1 x Underes mates? Impossible to tell?
- 34. Ques on ∫ 2 1 Es mate dx with L2 and R2 . Are your es mates overes mates? 1 x Underes mates? Impossible to tell? Answer Since the integrand is decreasing, ∫ 2 1 Rn < dx < Ln 1 x ∫ 2 7 1 5 for all n. So < dx < . 12 1 x 6
- 35. Outline Last me: The Definite Integral The definite integral as a limit Proper es of the integral Evalua ng Definite Integrals Examples The Integral as Net Change Indefinite Integrals My first table of integrals Compu ng Area with integrals
- 36. Socratic proof The definite integral of velocity measures displacement (net distance) The deriva ve of displacement is velocity So we can compute displacement with the definite integral or the an deriva ve of velocity But any func on can be a velocity func on, so . . .
- 37. Theorem of the Day Theorem (The Second Fundamental Theorem of Calculus) Suppose f is integrable on [a, b] and f = F′ for another func on F, then ∫ b f(x) dx = F(b) − F(a). a
- 38. Theorem of the Day Theorem (The Second Fundamental Theorem of Calculus) Suppose f is integrable on [a, b] and f = F′ for another func on F, then ∫ b f(x) dx = F(b) − F(a). a Note In Sec on 5.3, this theorem is called “The Evalua on Theorem”. Nobody else in the world calls it that.
- 39. Proving the Second FTC Proof. b−a Divide up [a, b] into n pieces of equal width ∆x = as n usual.
- 40. Proving the Second FTC Proof. b−a Divide up [a, b] into n pieces of equal width ∆x = as n usual. For each i, F is con nuous on [xi−1 , xi ] and differen able on (xi−1 , xi ). So there is a point ci in (xi−1 , xi ) with F(xi ) − F(xi−1 ) = F′ (ci ) = f(ci ) xi − xi−1
- 41. Proving the Second FTC Proof. b−a Divide up [a, b] into n pieces of equal width ∆x = as n usual. For each i, F is con nuous on [xi−1 , xi ] and differen able on (xi−1 , xi ). So there is a point ci in (xi−1 , xi ) with F(xi ) − F(xi−1 ) = F′ (ci ) = f(ci ) xi − xi−1 =⇒ f(ci )∆x = F(xi ) − F(xi−1 )
- 42. Proving the Second FTC Proof. Form the Riemann Sum:
- 43. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1
- 44. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 45. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 46. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 47. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 48. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 49. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 50. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 51. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 52. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 53. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 54. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 ))
- 55. Proving the Second FTC Proof. Form the Riemann Sum: ∑ n ∑ n Sn = f(ci )∆x = (F(xi ) − F(xi−1 )) i=1 i=1 = (F(x1 ) − F(x0 )) + (F(x2 ) − F(x1 )) + (F(x3 ) − F(x2 )) + · · · · · · + (F(xn−1 ) − F(xn−2 )) + (F(xn ) − F(xn−1 )) = F(xn ) − F(x0 ) = F(b) − F(a)
- 56. Proving the Second FTC Proof. We have shown for each n, Sn = F(b) − F(a) Which does not depend on n.
- 57. Proving the Second FTC Proof. We have shown for each n, Sn = F(b) − F(a) Which does not depend on n. So in the limit ∫ b f(x) dx = lim Sn = lim (F(b) − F(a)) = F(b) − F(a) a n→∞ n→∞
- 58. Computing area with the 2nd FTC Example Find the area between y = x3 and the x-axis, between x = 0 and x = 1. .
- 59. Computing area with the 2nd FTC Example Find the area between y = x3 and the x-axis, between x = 0 and x = 1. Solu on ∫ 1 1 3 x4 1 A= x dx = = 0 4 0 4 .
- 60. Computing area with the 2nd FTC Example Find the area between y = x3 and the x-axis, between x = 0 and x = 1. Solu on ∫ 1 1 3 x4 1 A= x dx = = 0 4 0 4 . Here we use the nota on F(x)|b or [F(x)]b to mean F(b) − F(a). a a
- 61. Computing area with the 2nd FTC Example Find the area enclosed by the parabola y = x2 and the line y = 1.
- 62. Computing area with the 2nd FTC Example Find the area enclosed by the parabola y = x2 and the line y = 1. 1 . −1 1
- 63. Computing area with the 2nd FTC Example Find the area enclosed by the parabola y = x2 and the line y = 1. Solu on ∫ 1 [ 3 ]1 x A=2− x dx = 2 − 2 1 3 −1 [−1 ( )] 1 1 4 =2− − − = . 3 3 3 −1 1
- 64. Computing an integral we estimated before Example ∫ 1 4 Evaluate the integral dx. 0 1 + x2
- 65. Example ∫ 1 4 Es mate dx using M4 . 0 1 + x2 Solu on ( ) 1 4 4 4 4 M4 = + + + 4 1 + (1/8)2 1 + (3/8)2 1 + (5/8)2 1 + (7/8)2 ( ) 1 4 4 4 4 = + + + 4 65/64 73/64 89/64 113/64 64 64 64 64 = + + + ≈ 3.1468 65 73 89 113
- 66. Computing an integral we estimated before Example ∫ 1 4 Evaluate the integral dx. 0 1 + x2 Solu on ∫ 1 ∫ 1 4 1 dx = 4 dx 0 1 + x2 0 1 + x2
- 67. Computing an integral we estimated before Example ∫ 1 4 Evaluate the integral dx. 0 1 + x2 Solu on ∫ 1 ∫ 1 4 1 dx = 4 dx = 4 arctan(x)|1 0 0 1 + x2 0 1 + x2
- 68. Computing an integral we estimated before Example ∫ 1 4 Evaluate the integral dx. 0 1 + x2 Solu on ∫ 1 ∫ 1 4 1 dx = 4 dx = 4 arctan(x)|1 0 0 1 + x2 0 1 + x2 = 4 (arctan 1 − arctan 0)
- 69. Computing an integral we estimated before Example ∫ 1 4 Evaluate the integral dx. 0 1 + x2 Solu on ∫ 1 ∫ 1 4 1 dx = 4 dx = 4 arctan(x)|1 0 1 + x2 0 1+x 2 0 (π ) = 4 (arctan 1 − arctan 0) = 4 −0 4
- 70. Computing an integral we estimated before Example ∫ 1 4 Evaluate the integral dx. 0 1 + x2 Solu on ∫ 1 ∫ 1 4 1 dx = 4 dx = 4 arctan(x)|1 0 1 + x2 0 1+x 2 0 (π ) = 4 (arctan 1 − arctan 0) = 4 −0 =π 4
- 71. Computing an integral we estimated before Example ∫ 2 1 Evaluate dx. 1 x
- 72. Example ∫ 2 1 Es mate dx using the comparison proper es. 1 x Solu on Since 1 1 1 ≤ ≤ 2 x 1 for all x in [1, 2], we have ∫ 2 1 1 ·1≤ dx ≤ 1 · 1 2 1 x
- 73. Computing an integral we estimated before Example ∫ 2 1 Evaluate dx. 1 x Solu on ∫ 2 1 dx 1 x
- 74. Computing an integral we estimated before Example ∫ 2 1 Evaluate dx. 1 x Solu on ∫ 2 1 dx = ln x|2 1 1 x
- 75. Computing an integral we estimated before Example ∫ 2 1 Evaluate dx. 1 x Solu on ∫ 2 1 dx = ln x|2 = ln 2 − ln 1 1 1 x
- 76. Computing an integral we estimated before Example ∫ 2 1 Evaluate dx. 1 x Solu on ∫ 2 1 dx = ln x|2 = ln 2 − ln 1 = ln 2 1 1 x
- 77. Outline Last me: The Definite Integral The definite integral as a limit Proper es of the integral Evalua ng Definite Integrals Examples The Integral as Net Change Indefinite Integrals My first table of integrals Compu ng Area with integrals
- 78. The Integral as Net Change Another way to state this theorem is: ∫ b F′ (x) dx = F(b) − F(a), a or the integral of a deriva ve along an interval is the net change over that interval. This has many interpreta ons.
- 79. The Integral as Net Change
- 80. The Integral as Net Change Corollary If v(t) represents the velocity of a par cle moving rec linearly, then ∫ t1 v(t) dt = s(t1 ) − s(t0 ). t0
- 81. The Integral as Net Change Corollary If MC(x) represents the marginal cost of making x units of a product, then ∫ x C(x) = C(0) + MC(q) dq. 0
- 82. The Integral as Net Change Corollary If ρ(x) represents the density of a thin rod at a distance of x from its end, then the mass of the rod up to x is ∫ x m(x) = ρ(s) ds. 0
- 83. Outline Last me: The Definite Integral The definite integral as a limit Proper es of the integral Evalua ng Definite Integrals Examples The Integral as Net Change Indefinite Integrals My first table of integrals Compu ng Area with integrals
- 84. A new notation for antiderivatives To emphasize the rela onship between an differen a on and integra on, we use the indefinite integral nota on ∫ f(x) dx for any func on whose deriva ve is f(x).
- 85. A new notation for antiderivatives To emphasize the rela onship between an differen a on and integra on, we use the indefinite integral nota on ∫ f(x) dx for any func on whose deriva ve is f(x). Thus ∫ x2 dx = 1 x3 + C. 3
- 86. My first table of integrals . ∫ ∫ ∫ [f(x) + g(x)] dx = f(x) dx + g(x) dx ∫ ∫ ∫ xn+1 xn dx = + C (n ̸= −1) cf(x) dx = c f(x) dx ∫ n+1 ∫ 1 ex dx = ex + C dx = ln |x| + C ∫ ∫ x ax sin x dx = − cos x + C ax dx = +C ∫ ln a ∫ cos x dx = sin x + C csc2 x dx = − cot x + C ∫ ∫ sec2 x dx = tan x + C csc x cot x dx = − csc x + C ∫ ∫ 1 sec x tan x dx = sec x + C √ dx = arcsin x + C ∫ 1 − x2 1 dx = arctan x + C 1 + x2
- 87. Outline Last me: The Definite Integral The definite integral as a limit Proper es of the integral Evalua ng Definite Integrals Examples The Integral as Net Change Indefinite Integrals My first table of integrals Compu ng Area with integrals
- 88. Computing Area with integrals Example Find the area of the region bounded by the lines x = 1, x = 4, the x-axis, and the curve y = ex .
- 89. Computing Area with integrals Example Find the area of the region bounded by the lines x = 1, x = 4, the x-axis, and the curve y = ex . Solu on The answer is ∫ 4 ex dx = ex |4 = e4 − e. 1 1
- 90. Computing Area with integrals Example Find the area of the region bounded by the curve y = arcsin x, the x-axis, and the line x = 1.
- 91. Computing Area with integrals Example Find the area of the region bounded by the curve y = arcsin x, the x-axis, and the line x = 1. Solu on y ∫ 1 The answer is arcsin x dx, but π/2 0 we do not know an an deriva ve for arcsin. . x 1
- 92. Computing Area with integrals Example Find the area of the region bounded by the curve y = arcsin x, the x-axis, and the line x = 1. Solu on y Instead compute the area as π/2 ∫ π/2 π − sin y dy 2 0 . x 1
- 93. Computing Area with integrals Example Find the area of the region bounded by the curve y = arcsin x, the x-axis, and the line x = 1. Solu on y Instead compute the area as π/2 ∫ π/2 π π π/2 − sin y dy = −[− cos x]0 2 0 2 . x 1
- 94. Computing Area with integrals Example Find the area of the region bounded by the curve y = arcsin x, the x-axis, and the line x = 1. Solu on y Instead compute the area as π/2 ∫ π/2 π π π/2 π − sin y dy = −[− cos x]0 = −1 2 0 2 2 . x 1
- 95. Example Find the area between the graph of y = (x − 1)(x − 2), the x-axis, and the ver cal lines x = 0 and x = 3.
- 96. Example Find the area between the graph of y = (x − 1)(x − 2), the x-axis, and the ver cal lines x = 0 and x = 3. Solu on No ce the func on y = (x − 1)(x − 2) is posi ve on [0, 1) y and (2, 3], and nega ve on (1, 2). . x 1 2 3
- 97. Example Find the area between the graph of y = (x − 1)(x − 2), the x-axis, and the ver cal lines x = 0 and x = 3. Solu on ∫ 1 A= (x2 − 3x + 2) dx y 0 ∫ 2 − (x2 − 3x + 2) dx 1 ∫ 3 . x + (x2 − 3x + 2) dx 1 2 3 2
- 98. Example Find the area between the graph of y = (x − 1)(x − 2), the x-axis, and the ver cal lines x = 0 and x = 3. Solu on ∫ 1 A= (x − 1)(x − 2) dx y 0 ∫ 2 − (x − 1)(x − 2) dx 1 ∫ 3 . x + (x − 1)(x − 2) dx 1 2 3 2
- 99. Example Find the area between the graph of y = (x − 1)(x − 2), the x-axis, and the ver cal lines x = 0 and x = 3. Solu on [1 ]1 y A= 3 x − 3 x2 + 2x 0 3 2 [1 3 3 2 ]2 − 3x − 2x + 2x 1 [ ]3 + 1 x3 − 3 x2 + 3 2 2x 2 . x 11 1 2 3 = 6
- 100. Interpretation of “negative area” in motion There is an analog in rectlinear mo on: ∫ t1 v(t) dt is net distance traveled. t0 ∫ t1 |v(t)| dt is total distance traveled. t0
- 101. What about the constant? It seems we forgot about the +C when we say for instance ∫ 1 1 x4 1 1 3 x dx = = −0= 0 4 0 4 4 But no ce [ 4 ]1 ( ) x 1 1 1 +C = + C − (0 + C) = + C − C = 4 0 4 4 4 no ma er what C is. So in an differen a on for definite integrals, the constant is immaterial.
- 102. Summary The second Fundamental Theorem of Calculus: ∫ b f(x) dx = F(b) − F(a) a where F′ = f. Definite integrals represent net change of a func on over an interval. ∫ We write an deriva ves as indefinite integrals f(x) dx





![The definite integral as a limit
Defini on
If f is a func on defined on [a, b], the definite integral of f from a to
b is the number
∫ b ∑n
f(x) dx = lim f(ci ) ∆x
a n→∞
i=1
b−a
where ∆x = , and for each i, xi = a + i∆x, and ci is a point in
n
[xi−1 , xi ].](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-5-320.jpg)
![The definite integral as a limit
Theorem
If f is con nuous on [a, b] or if f has only finitely many jump
discon nui es, then f is integrable on [a, b]; that is, the definite
∫ b
integral f(x) dx exists and is the same for any choice of ci .
a](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-6-320.jpg)






![Properties of the integral
Theorem (Addi ve Proper es of the Integral)
Let f and g be integrable func ons on [a, b] and c a constant. Then
∫ b
1. c dx = c(b − a)
a
∫ b ∫ b ∫ b
2. [f(x) + g(x)] dx = f(x) dx + g(x) dx.
a a a
∫ b ∫ b
3. cf(x) dx = c f(x) dx.
∫a b a
∫ b ∫ b
4. [f(x) − g(x)] dx = f(x) dx − g(x) dx.
a a a](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-13-320.jpg)







![Comparison Properties of the Integral
Theorem
Let f and g be integrable func ons on [a, b].](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-24-320.jpg)
![Comparison Properties of the Integral
Theorem
Let f and g be integrable func ons on [a, b].
∫ b
6. If f(x) ≥ 0 for all x in [a, b], then f(x) dx ≥ 0
a](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-25-320.jpg)
![Comparison Properties of the Integral
Theorem
Let f and g be integrable func ons on [a, b].
∫ b
6. If f(x) ≥ 0 for all x in [a, b], then f(x) dx ≥ 0
a
∫ b ∫ b
7. If f(x) ≥ g(x) for all x in [a, b], then f(x) dx ≥ g(x) dx
a a](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-26-320.jpg)
![Comparison Properties of the Integral
Theorem
Let f and g be integrable func ons on [a, b].
∫ b
6. If f(x) ≥ 0 for all x in [a, b], then f(x) dx ≥ 0
a
∫ b ∫ b
7. If f(x) ≥ g(x) for all x in [a, b], then f(x) dx ≥ g(x) dx
a a
8. If m ≤ f(x) ≤ M for all x in [a, b], then
∫ b
m(b − a) ≤ f(x) dx ≤ M(b − a)
a](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-27-320.jpg)
![Integral of a nonnegative function is nonnegative
Proof.
If f(x) ≥ 0 for all x in [a, b], then for
any number of divisions n and choice
of sample points {ci }:
∑
n ∑
n
Sn = f(ci ) ∆x ≥ 0 · ∆x = 0
i=1 ≥0 i=1
. x
Since Sn ≥ 0 for all n, the limit of {Sn } is nonnega ve, too:
∫ b
f(x) dx = lim Sn ≥ 0
a n→∞
≥0](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-28-320.jpg)
![The integral is “increasing”
Proof.
Let h(x) = f(x) − g(x). If f(x) ≥ g(x)
for all x in [a, b], then h(x) ≥ 0 for all f(x)
x in [a, b]. So by the previous h(x) g(x)
property
∫ b
h(x) dx ≥ 0 . x
a
This means that
∫ b ∫ b ∫ b ∫ b
f(x) dx − g(x) dx = (f(x) − g(x)) dx = h(x) dx ≥ 0
a a a a](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-29-320.jpg)
![Bounding the integral
Proof.
If m ≤ f(x) ≤ M on for all x in [a, b], then by
y
the previous property
∫ b ∫ b ∫ b M
m dx ≤ f(x) dx ≤ M dx
a a a f(x)
By Property 8, the integral of a constant
func on is the product of the constant and m
the width of the interval. So:
∫ b . x
m(b − a) ≤ f(x) dx ≤ M(b − a) a b
a](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-30-320.jpg)

![Example
∫ 2
1
Es mate dx using the comparison proper es.
1 x
Solu on
Since
1 1 1
≤ ≤
2 x 1
for all x in [1, 2], we have
∫ 2
1 1
·1≤ dx ≤ 1 · 1
2 1 x](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-32-320.jpg)




![Theorem of the Day
Theorem (The Second Fundamental Theorem of Calculus)
Suppose f is integrable on [a, b] and f = F′ for another func on F,
then ∫ b
f(x) dx = F(b) − F(a).
a](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-37-320.jpg)
![Theorem of the Day
Theorem (The Second Fundamental Theorem of Calculus)
Suppose f is integrable on [a, b] and f = F′ for another func on F,
then ∫ b
f(x) dx = F(b) − F(a).
a
Note
In Sec on 5.3, this theorem is called “The Evalua on Theorem”.
Nobody else in the world calls it that.](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-38-320.jpg)
![Proving the Second FTC
Proof.
b−a
Divide up [a, b] into n pieces of equal width ∆x = as
n
usual.](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-39-320.jpg)
![Proving the Second FTC
Proof.
b−a
Divide up [a, b] into n pieces of equal width ∆x = as
n
usual.
For each i, F is con nuous on [xi−1 , xi ] and differen able on
(xi−1 , xi ). So there is a point ci in (xi−1 , xi ) with
F(xi ) − F(xi−1 )
= F′ (ci ) = f(ci )
xi − xi−1](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-40-320.jpg)
![Proving the Second FTC
Proof.
b−a
Divide up [a, b] into n pieces of equal width ∆x = as
n
usual.
For each i, F is con nuous on [xi−1 , xi ] and differen able on
(xi−1 , xi ). So there is a point ci in (xi−1 , xi ) with
F(xi ) − F(xi−1 )
= F′ (ci ) = f(ci )
xi − xi−1
=⇒ f(ci )∆x = F(xi ) − F(xi−1 )](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-41-320.jpg)


















![Computing area with the 2nd FTC
Example
Find the area between y = x3 and the x-axis, between x = 0 and
x = 1.
Solu on
∫ 1 1
3 x4 1
A= x dx = =
0 4 0 4 .
Here we use the nota on F(x)|b or [F(x)]b to mean F(b) − F(a).
a a](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-60-320.jpg)


![Computing area with the 2nd FTC
Example
Find the area enclosed by the parabola y = x2 and the line y = 1.
Solu on
∫ 1 [ 3 ]1
x
A=2− x dx = 2 −
2
1
3 −1
[−1 ( )]
1 1 4
=2− − − = .
3 3 3
−1 1](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-63-320.jpg)








![Example
∫ 2
1
Es mate dx using the comparison proper es.
1 x
Solu on
Since
1 1 1
≤ ≤
2 x 1
for all x in [1, 2], we have
∫ 2
1 1
·1≤ dx ≤ 1 · 1
2 1 x](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-72-320.jpg)













![My first table of integrals
.
∫ ∫ ∫
[f(x) + g(x)] dx = f(x) dx + g(x) dx
∫ ∫ ∫
xn+1
xn dx = + C (n ̸= −1) cf(x) dx = c f(x) dx
∫ n+1 ∫
1
ex dx = ex + C dx = ln |x| + C
∫ ∫ x
ax
sin x dx = − cos x + C ax dx = +C
∫ ln a
∫
cos x dx = sin x + C csc2 x dx = − cot x + C
∫ ∫
sec2 x dx = tan x + C csc x cot x dx = − csc x + C
∫ ∫
1
sec x tan x dx = sec x + C √ dx = arcsin x + C
∫ 1 − x2
1
dx = arctan x + C
1 + x2](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-86-320.jpg)






![Computing Area with integrals
Example
Find the area of the region bounded by the curve y = arcsin x, the
x-axis, and the line x = 1.
Solu on
y
Instead compute the area as π/2
∫ π/2
π π π/2
− sin y dy = −[− cos x]0
2 0 2
.
x
1](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-93-320.jpg)
![Computing Area with integrals
Example
Find the area of the region bounded by the curve y = arcsin x, the
x-axis, and the line x = 1.
Solu on
y
Instead compute the area as π/2
∫ π/2
π π π/2 π
− sin y dy = −[− cos x]0 = −1
2 0 2 2
.
x
1](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-94-320.jpg)

![Example
Find the area between the graph of y = (x − 1)(x − 2), the x-axis,
and the ver cal lines x = 0 and x = 3.
Solu on
No ce the func on
y = (x − 1)(x − 2) is posi ve on [0, 1) y
and (2, 3], and nega ve on (1, 2).
. x
1 2 3](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-96-320.jpg)


![Example
Find the area between the graph of y = (x − 1)(x − 2), the x-axis,
and the ver cal lines x = 0 and x = 3.
Solu on
[1 ]1 y
A= 3 x − 3 x2 + 2x 0
3
2
[1 3 3 2 ]2
− 3x − 2x + 2x 1
[ ]3
+ 1 x3 − 3 x2 +
3 2 2x 2 . x
11 1 2 3
=
6](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-99-320.jpg)

![What about the constant?
It seems we forgot about the +C when we say for instance
∫ 1 1
x4 1 1
3
x dx = = −0=
0 4 0 4 4
But no ce
[ 4 ]1 ( )
x 1 1 1
+C = + C − (0 + C) = + C − C =
4 0 4 4 4
no ma er what C is.
So in an differen a on for definite integrals, the constant is
immaterial.](https://image.slidesharecdn.com/lesson25-evaluatingdefiniteintegrals011slides-110501232322-phpapp02/85/Lesson-25-Evaluating-Definite-Integrals-slides-101-320.jpg)
