![linear programing
BUILDING ENGINEERING AND MANAGEMENT
Quantitative Methods and Operation Research [MBEM -112]
Deepak Pradhan
1210900048](https://image.slidesharecdn.com/linearprograming-211227143752/85/Linear-programing-1-320.jpg)
![FORMS of Linear Programing
The canonical form
• Objective function is of maximum type
• All decision variables are non negative
The Standard Form
• All variables are non negative
• The right hand side of each constraint is non negative.
• All constraints are expressed in equations.
• Objective function may be of maximization or minimization
type.
Important Definitions in Linear Programming
Solution:
A set of variables [X1 ,X2,...,Xn+m] is called a
solution to L.P. Problem if it satisfies its constraints.
Feasible Solution:
A set of variables [X1 ,X2,...,Xn+m] is called a
feasible solution to L.P. Problem if it satisfies its
constraints as well as non-negativity restrictions.
Optimal Feasible Solution:
The basic feasible solution that optimises the
objective function.
Unbounded Solution:
If the value of the objective function can be
increased or decreased indefinitely, the solution is called
an unbounded solution.](https://image.slidesharecdn.com/linearprograming-211227143752/85/Linear-programing-7-320.jpg)
Linear programing
- 1. linear programing BUILDING ENGINEERING AND MANAGEMENT Quantitative Methods and Operation Research [MBEM -112] Deepak Pradhan 1210900048
- 2. INTRODUCTION LINEAR PROGRAMMING • Linear programming uses a mathematical model to describe the problem of concern. • The word linear means the relationship which can be represented by a straight line .i.e the relation is of the form • ax +by=c. In other words it is used to describe the relationship between two or more variables which are proportional to each other. The word "programming" is concerned with the optimal allocation of limited resources. Linear programming is a way to handle certain types of optimization problems Linear programming is a mathematical method for determining a way to achieve the best outcome. Linear programing planning • A mathematical technique used to obtain an optimum solution in resource allocation problems, such as production planning. • It is a mathematical model or technique for efficient and effective utilization of limited recourses to achieve organization objectives (Maximize profits or Minimize cost). • When solving a problem using linear programming the program is put into a number of linear inequalities and then an attempt is made to maximize (or minimize) the inputs. REQUIREMENTS • There must be well defined objective function. • There must be a constraint on the amount. • There must be alternative course of action. • The decision variables should be interrelated and non negative. • The resource must be limited in supply. ASSUMPTIONS Proportionality Additivity Continuity Certainty Finite Choices
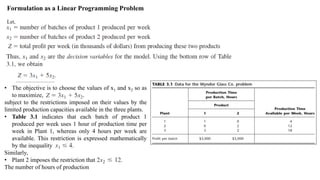
- 3. Formulation as a Linear Programming Problem Let, • The objective is to choose the values of x1 and x2 so as to maximize, subject to the restrictions imposed on their values by the limited production capacities available in the three plants. • Table 3.1 indicates that each batch of product 1 produced per week uses 1 hour of production time per week in Plant 1, whereas only 4 hours per week are available. This restriction is expressed mathematically by the inequality Similarly, • Plant 2 imposes the restriction that The number of hours of production
- 4. • Time used per week in Plant 3 by choosing x1 and x2 as the new products’ production rates would be . Therefore, the mathematical statement of the Plant 3 restriction is • Finally, since production rates cannot be negative, it is necessary to restrict the decision variables to be non-negative: • To summarize, in the mathematical language of linear programming, the problem is to choose values of x1 and x2 so as to Graphical Solution The final step is to pick out the point in this feasible region that maximizes the value of Z = 3x1 + 5x2.
- 5. To discover how to perform this step efficiently, begin by trial and error. Try, • for example, Z =10 = 3x1 + 5x2 to see if there are in the permissible region any values of (x1, x2) that yield a value of Z as large as 10. • next try a larger arbitrary value of Z, say, Z =20 = 3x1 + 5x2 . Again This last equation, called the slope-intercept form The value of (x1, x2) that maximizes 3x1 + 5x2 is (2, 6). Indicating that the optimal solution is x1 = 2 and x2 = 6. The equation of this line is 3x1 + 5x2 = 3(2) + 5(6) = 36 = Z, indicating that the optimal value of Z is Z = 36
- 6. The linear programming MODEL • The model poses the problem in terms of making decisions about the levels of the activities, so x1, x2, . . . , xn are called the Decision variables. A Standard Form of the Model Z = value of overall measure of performance. xj = level of activity j (for j = 1, 2, . . . , n). cj = increase in Z that would result from each unit increase in level of activity j. bi = amount of resource i that is available for allocation to activities (for i = 1, 2, . . . , m). aij = amount of resource i consumed by each unit of activity j.
- 7. FORMS of Linear Programing The canonical form • Objective function is of maximum type • All decision variables are non negative The Standard Form • All variables are non negative • The right hand side of each constraint is non negative. • All constraints are expressed in equations. • Objective function may be of maximization or minimization type. Important Definitions in Linear Programming Solution: A set of variables [X1 ,X2,...,Xn+m] is called a solution to L.P. Problem if it satisfies its constraints. Feasible Solution: A set of variables [X1 ,X2,...,Xn+m] is called a feasible solution to L.P. Problem if it satisfies its constraints as well as non-negativity restrictions. Optimal Feasible Solution: The basic feasible solution that optimises the objective function. Unbounded Solution: If the value of the objective function can be increased or decreased indefinitely, the solution is called an unbounded solution.
- 8. ADVANTAGES . • By converting a primal problem into dual computation becomes easier , as the no. of rows(constraints) reduces in comparison with the no. of columns( variables). • Gives additional information as to how the optimal solution changes as a result of the changes in the coefficients. This is the basis for sensitivity analysis. • Economic interpretation of dual helps the management in making future decisions. • Duality is used to solve L.P. problems in which the initial solution in infeasible. SENSITIVITY ANALYSIS . (POST OPTIMALITY TEST) Two situations: • In formulation , it is assumed that the parameters such as market demand, equipment capacity, resource consumption, costs, profits etc., do not change but in real time it is not possible. • After attaining the optimal solution, one may discover that a wrong value of a cost coefficient was used or a particular variable or constraint was omitted etc., • Changes in the parameters of the problem may be discrete or continuous. • The study of effect of discrete changes in parameters on the optimal solution is called as "Sensitivity analysis". • The study of effect of continuous changes in parameters • on the optimal solution is called as "Parametric Programming." • The objective of the sensitivity analysis is to determine how sensitive is the optimal solution to the changes in the parameters.
- 9. AREAS OF APPLICATION OF LINEAR PROGRAMMING Industrial Application • Product Mix Problem • Blending Problems • Production Scheduling Problem • Assembly Line Balancing • Make-Or-Buy Problems • Management Applications Media Selection Problems • Portfolio Selection Problems • Profit Planning Problems • Transportation Problems • Miscellaneous Applications Diet Problems • Agriculture Problems • Flight Scheduling Problems • Facilities Location Problems Advantages of linear programming • It helps in attaining optimum use of productive factors. • It improves the quality of the decisions. • It provides better tools for meeting the changing conditions. • It highlights the bottleneck in the production process. Limitation of linear programming • For large problems the computational difficulties are enormous. • It may yield fractional value answers to decision variables. • It is applicable to only static situation. • LP deals with the problems with single objective.
- 10. Thank you