Linear Regression
8 likes•1,126 views
This document is an introduction to statistical machine learning presented by Christfried Webers from NICTA and The Australian National University. It discusses linear basis function models and how to perform maximum likelihood and least squares estimation. Specifically, it shows that maximizing the likelihood is equivalent to minimizing the sum-of-squares error, and that the maximum likelihood solution is given by the pseudo-inverse of the design matrix. It also examines the geometry of least squares and the bias-variance decomposition.
![Introduction to Statistical
Maximum Likelihood and Least Squares Machine Learning
c 2011
Christfried Webers
NICTA
Found a critical point wML for ln p(t | w, β). Is it a maximum, The Australian National
University
a minimum, or a saddle point?
Calculate the second directional derivative
D2 ln p(t | w, β)(ξ, ξ) = −β ξ T ΦT Φξ
= −β (Φξ)T Φξ Linear Basis Function
Models
2
= −β Φξ ≤0 Maximum Likelihood and
Least Squares
Geometry of Least
We found a maximum. Squares
(Is it enough to check the second directional derivative in Sequential Learning
two directions ξ which are the same? Yes, because for any Regularized Least
Squares
bilinear function g(ξ, η), symmetric in its arguments, Multiple Outputs
Loss Function for
1 Regression
[g(ξ, ξ) + g(η, η) − g(ξ − η, ξ − η)]
2 The Bias-Variance
Decomposition
1
= [g(ξ, ξ) + g(η, η) − g(ξ, ξ) − g(η, η) + g(ξ, η) + g(η, ξ)]
2
1
= [g(ξ, η) + g(η, ξ)] = g(ξ, η)
2
172of 197](https://image.slidesharecdn.com/linear-regression4566-120929062550-phpapp01/85/Linear-Regression-15-320.jpg)
![Introduction to Statistical
Loss Function for Regression Machine Learning
c 2011
Christfried Webers
NICTA
The Australian National
University
Choose an estimator y(x) to estimate the target value t for
each input x.
Choose a loss function L(t, y(x)) which measures the
difference between the target t and the estimate y(x).
Linear Basis Function
The expected loss is then Models
Maximum Likelihood and
Least Squares
E [L] = L(t, y(x)) p(x, t) dx dt Geometry of Least
Squares
Sequential Learning
Common choice: Squared Loss Regularized Least
Squares
2
L(t, y(x)) = {y(x) − t} . Multiple Outputs
Loss Function for
Regression
Expected loss for squared loss function The Bias-Variance
Decomposition
2
E [L] = {y(x) − t} p(x, t) dx dt.
184of 197](https://image.slidesharecdn.com/linear-regression4566-120929062550-phpapp01/85/Linear-Regression-27-320.jpg)
![Introduction to Statistical
Loss Function for Regression Machine Learning
c 2011
Christfried Webers
NICTA
The Australian National
University
Expected loss for squared loss function
Linear Basis Function
2 Models
E [L] = {y(x) − t} p(x, t) dx dt.
Maximum Likelihood and
Least Squares
Minimise E [L] by choosing the regression function Geometry of Least
Squares
Sequential Learning
t p(x, t) dt Regularized Least
y(x) = = t p(t | x) dt = Et [t | x] Squares
p(x)
Multiple Outputs
Loss Function for
(use calculus of variations to derive this result). Regression
The Bias-Variance
Decomposition
185of 197](https://image.slidesharecdn.com/linear-regression4566-120929062550-phpapp01/85/Linear-Regression-28-320.jpg)
![Introduction to Statistical
Loss Function for Regression Machine Learning
c 2011
Christfried Webers
NICTA
The Australian National
University
Analyse the expected loss
2
E [L] = {y(x) − t} p(x, t) dx dt.
Linear Basis Function
Models
Rewrite the squared loss Maximum Likelihood and
Least Squares
2 2
{y(x) − t} = {y(x) − E [t | x] + E [t | x] − t} Geometry of Least
Squares
2 2
= {y(x) − E [t | x]} + {E [t | x] − t} Sequential Learning
Regularized Least
+ 2 {y(x) − E [t | x]} {E [t | x] − t} Squares
Multiple Outputs
Claim Loss Function for
Regression
The Bias-Variance
{y(x) − E [t | x]} {E [t | x] − t} p(x, t) dx dt = 0. Decomposition
187of 197](https://image.slidesharecdn.com/linear-regression4566-120929062550-phpapp01/85/Linear-Regression-30-320.jpg)
![Introduction to Statistical
Loss Function for Regression Machine Learning
c 2011
Christfried Webers
NICTA
The Australian National
University
Claim
{y(x) − E [t | x]} {E [t | x] − t} p(x, t) dx dt = 0.
Seperate functions depending on t from function Linear Basis Function
Models
depending on x Maximum Likelihood and
Least Squares
Geometry of Least
{y(x) − E [t | x]} {E [t | x] − t} p(x, t) dt dx Squares
Sequential Learning
Regularized Least
Calculate the integral over t Squares
Multiple Outputs
t p(x, t) Loss Function for
{E [t | x] − t} p(x, t) dt = E [t | x] p(x) − p(x) dt Regression
p(x) The Bias-Variance
Decomposition
= E [t | x] p(x) − p(x)E [t | x]
=0
188of 197](https://image.slidesharecdn.com/linear-regression4566-120929062550-phpapp01/85/Linear-Regression-31-320.jpg)
![Introduction to Statistical
Loss Function for Regression Machine Learning
c 2011
Christfried Webers
NICTA
The Australian National
University
The expected loss is now
Linear Basis Function
Models
2
E [L] = {y(x) − E [t | x]} p(x) dx + var[t | x] p(x) dx Maximum Likelihood and
Least Squares
Geometry of Least
Squares
Minimise first term by choosing appropriate y(x).
Sequential Learning
Second term represents the intrinsic variability of the Regularized Least
Squares
target data (can be regarded as noise). Independent of the
Multiple Outputs
choice y(x), can not be reduced by learning a better y(x).
Loss Function for
Regression
The Bias-Variance
Decomposition
189of 197](https://image.slidesharecdn.com/linear-regression4566-120929062550-phpapp01/85/Linear-Regression-32-320.jpg)
![Introduction to Statistical
The Bias-Variance Decomposition Machine Learning
c 2011
Christfried Webers
NICTA
The Australian National
University
Consider now the dependency on the data set D.
Prediction function now y(x; D).
Consider again squared loss for which the optimal Linear Basis Function
Models
prediction is given by the conditional expectation h(x) Maximum Likelihood and
Least Squares
Geometry of Least
h(x) = E [t | x] = t p(t | x) dt. Squares
Sequential Learning
Regularized Least
BUT: we can not know h(x) exactly, as we would need an Squares
infinite number of training data to learn it accurately. Multiple Outputs
Loss Function for
Evaluate performance of algorithm by taking the Regression
expectation ED [L] over all data sets D The Bias-Variance
Decomposition
190of 197](https://image.slidesharecdn.com/linear-regression4566-120929062550-phpapp01/85/Linear-Regression-33-320.jpg)
![Introduction to Statistical
The Bias-Variance Decomposition Machine Learning
c 2011
Christfried Webers
NICTA
The Australian National
University
Taking the expectation over all data sets D
ED [E [L]] = ED {y(x; D) − h(x)}2 p(x) dx
Linear Basis Function
Models
+ {h(x) − t}2 p(x, t) dx dt Maximum Likelihood and
Least Squares
Geometry of Least
Squares
Again, add and subtract the expectation ED [y(x; D)] Sequential Learning
Regularized Least
{y(x; D) − h(x)}2 = { y(x; D) − ED [y(x; D)] Squares
Multiple Outputs
+ ED [y(x; D)] − h(x)}2 Loss Function for
Regression
and show that the mixed term does vanish under the The Bias-Variance
Decomposition
expectation ED [. . .].
191of 197](https://image.slidesharecdn.com/linear-regression4566-120929062550-phpapp01/85/Linear-Regression-34-320.jpg)
![Introduction to Statistical
The Bias-Variance Decomposition Machine Learning
c 2011
Christfried Webers
NICTA
The Australian National
University
Expected loss ED [L] over all data sets D
expected loss = (bias)2 + variance + noise.
where Linear Basis Function
Models
2
(bias)2 = {ED [y(x; D)] − h(x)} p(x) dx Maximum Likelihood and
Least Squares
Geometry of Least
Squares
2
variance = ED {y(x; D) − ED [y(x; D)]} p(x) dx Sequential Learning
Regularized Least
Squares
noise = {h(x) − t}2 p(x, t) dx dt. Multiple Outputs
Loss Function for
Regression
squared bias : how much does the average prediction over
The Bias-Variance
all data sets differ from the desired regression function ? Decomposition
variance : how much do solutions for individual data sets
vary around their average ?
192of 197](https://image.slidesharecdn.com/linear-regression4566-120929062550-phpapp01/85/Linear-Regression-35-320.jpg)
Linear Regression
- 1. Introduction to Statistical Machine Learning c 2011 Christfried Webers NICTA The Australian National University Introduction to Statistical Machine Learning Christfried Webers Statistical Machine Learning Group NICTA and College of Engineering and Computer Science The Australian National University Canberra February – June 2011 (Many figures from C. M. Bishop, "Pattern Recognition and Machine Learning") 1of 197
- 2. Introduction to Statistical Machine Learning c 2011 Christfried Webers NICTA The Australian National University Part V Linear Basis Function Models Maximum Likelihood and Linear Regression 1 Least Squares Geometry of Least Squares Sequential Learning Regularized Least Squares Multiple Outputs Loss Function for Regression The Bias-Variance Decomposition 159of 197
- 3. Introduction to Statistical Regression Machine Learning c 2011 Christfried Webers NICTA The Australian National University Given a training data set of N observations {xn } and target values tn . Goal : Learn to predict the value of one ore more target values t given a new value of the input x. Linear Basis Function Models Example: Polynomial curve fitting (see Introduction). Maximum Likelihood and Least Squares t Geometry of Least Squares Sequential Learning Regularized Least Squares Multiple Outputs ? Loss Function for Regression The Bias-Variance Decomposition x 160of 197
- 4. Introduction to Statistical Supervised Learning Machine Learning c 2011 Christfried Webers NICTA The Australian National Training Phase University training model with adjustable data x parameter w Linear Basis Function Models training Maximum Likelihood and targets Least Squares t Geometry of Least Squares Sequential Learning fix the most appropriate w* Regularized Least Squares Test Phase Multiple Outputs Loss Function for Regression test test model with fixed target The Bias-Variance data x parameter w* Decomposition t 161of 197
- 5. Introduction to Statistical Linear Basis Function Models Machine Learning c 2011 Christfried Webers NICTA The Australian National University Linear combination of fixed nonlinear basis functions M−1 Linear Basis Function Models y(x, w) = wj φj (x) = wT φ(x) Maximum Likelihood and Least Squares j=0 Geometry of Least Squares T parameter w = (w0 , . . . , wM−1 ) Sequential Learning basis functions φ = (φ0 , . . . , φM−1 )T Regularized Least Squares convention φ0 (x) = 1 Multiple Outputs w0 is the bias parameter Loss Function for Regression The Bias-Variance Decomposition 162of 197
- 6. Introduction to Statistical Polynomial Basis Functions Machine Learning c 2011 Christfried Webers NICTA Scalar input variable x The Australian National University φj (x) = xj Limitation : Polynomials are global functions of the input variable x. Extension: Split the input space into regions and fit a Linear Basis Function different polynomial to each region (spline functions). Models Maximum Likelihood and Least Squares 1 Geometry of Least Squares Sequential Learning 0.5 Regularized Least Squares Multiple Outputs 0 Loss Function for Regression −0.5 The Bias-Variance Decomposition −1 −1 0 1 163of 197
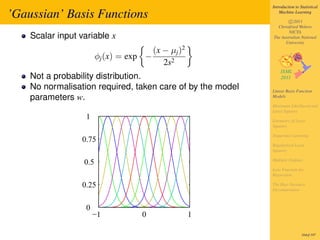
- 7. Introduction to Statistical ’Gaussian’ Basis Functions Machine Learning c 2011 Christfried Webers NICTA Scalar input variable x The Australian National University (x − µj )2 φj (x) = exp − 2s2 Not a probability distribution. No normalisation required, taken care of by the model Linear Basis Function parameters w. Models Maximum Likelihood and Least Squares 1 Geometry of Least Squares Sequential Learning 0.75 Regularized Least Squares Multiple Outputs 0.5 Loss Function for Regression 0.25 The Bias-Variance Decomposition 0 −1 0 1 164of 197
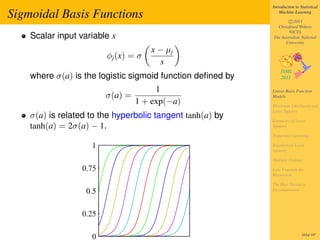
- 8. Introduction to Statistical Sigmoidal Basis Functions Machine Learning c 2011 Christfried Webers NICTA Scalar input variable x The Australian National University x − µj φj (x) = σ s where σ(a) is the logistic sigmoid function defined by 1 Linear Basis Function σ(a) = Models 1 + exp(−a) Maximum Likelihood and Least Squares σ(a) is related to the hyperbolic tangent tanh(a) by Geometry of Least tanh(a) = 2σ(a) − 1. Squares Sequential Learning 1 Regularized Least Squares Multiple Outputs 0.75 Loss Function for Regression The Bias-Variance 0.5 Decomposition 0.25 0 165of 197
- 9. Introduction to Statistical Other Basis Functions Machine Learning c 2011 Christfried Webers NICTA The Australian National University Fourier Basis : each basis function represents a specific Linear Basis Function Models frequency and has infinite spatial extent. Maximum Likelihood and Least Squares Wavelets : localised in both space and frequency (also Geometry of Least mutually orthogonal to simplify appliciation). Squares Sequential Learning Splines (polynomials restricted to regions of the input Regularized Least space). Squares Multiple Outputs Loss Function for Regression The Bias-Variance Decomposition 166of 197
- 10. Introduction to Statistical Maximum Likelihood and Least Squares Machine Learning c 2011 Christfried Webers NICTA The Australian National University No special assumption about the basis functions φj (x). In the simplest case, one can think of φj (x) = x. Linear Basis Function Assume target t is given by Models Maximum Likelihood and t = y(x, w) + Least Squares Geometry of Least deterministic noise Squares Sequential Learning where is a zero-mean Gaussian random variable with Regularized Least Squares precision (inverse variance) β. Multiple Outputs Thus Loss Function for Regression p(t | x, w, β) = N (t | y(x, w), β −1 ) The Bias-Variance Decomposition 167of 197
- 11. Introduction to Statistical Maximum Likelihood and Least Squares Machine Learning c 2011 Christfried Webers NICTA The Australian National Likelihood of one target t given the data x University p(t | x, w, β) = N (t | y(x, w), β −1 ) Set of inputs X with corresponding target values t. Linear Basis Function Assume data are independent and identically distributed Models (i.i.d.) (means : data are drawn independent and from the Maximum Likelihood and Least Squares same distribution). The likelihood of the target t is then Geometry of Least Squares N Sequential Learning p(t | X, w, β) = N (tn | y(xn , w), β −1 ) Regularized Least Squares n=1 Multiple Outputs N T −1 Loss Function for = N (tn | w φ(xn ), β ) Regression n=1 The Bias-Variance Decomposition From now on drop the conditioning variable X from the notation, as with supervised learning we do not seek to model the distribution of the input data. 168of 197
- 12. Introduction to Statistical Maximum Likelihood and Least Squares Machine Learning c 2011 Christfried Webers NICTA The Australian National Consider the logarithm of the likelihood p(t | w, β) (the University logarithm is a monoton function! ) N ln p(t | w, β) = ln N (tn | wT φ(xn ), β −1 ) Linear Basis Function n=1 Models N β β Maximum Likelihood and = ln exp − (tn − wT φ(xn ))2 Least Squares 2π 2 Geometry of Least n=1 Squares N N Sequential Learning = ln β − ln(2π) − βED (w) 2 2 Regularized Least Squares Multiple Outputs where the sum-of-squares error function is Loss Function for Regression N 1 The Bias-Variance ED (w) = {tn − wT φ(xn )}2 . Decomposition 2 n=1 arg maxw ln p(t | w, β) → arg minw ED (w) 169of 197
- 13. Introduction to Statistical Maximum Likelihood and Least Squares Machine Learning c 2011 Christfried Webers NICTA The Australian National University Rewrite the Error Function N 1 1 ED (w) = {tn − wT φ(xn )}2 = (t − Φw)T (t − Φw) Linear Basis Function 2 2 Models n=1 Maximum Likelihood and Least Squares T where t = (t1 , . . . , tN ) , and Geometry of Least Squares φ0 (x1 ) φ1 (x1 ) ... φM−1 (x1 ) Sequential Learning φ0 (x2 ) φ1 (x2 ) ... φM−1 (x2 ) Regularized Least Squares Φ= . . .. . . . . Multiple Outputs . . . . Loss Function for Regression φ0 (xN ) φ1 (xN ) ... φM−1 (xN ) The Bias-Variance Decomposition 170of 197
- 14. Introduction to Statistical Maximum Likelihood and Least Squares Machine Learning c 2011 Christfried Webers NICTA The log likelihood is now The Australian National University N N ln p(t | w, β) =ln β − ln(2π) − βED (w) 2 2 N N 1 = ln β − ln(2π) − β (t − Φw)T (t − Φw) 2 2 2 Linear Basis Function Models Find critical points of ln p(t | w, β). Maximum Likelihood and Least Squares Directional derivative in direction ξ Geometry of Least Squares D ln p(t | w, β)(ξ) = βξ T (ΦT t − ΦT Φw) Sequential Learning Regularized Least shall be zero in all directions ξ. Therefore Squares Multiple Outputs 0 = ΦT t − ΦT Φw, Loss Function for Regression which results in The Bias-Variance Decomposition wML = (ΦT Φ)−1 ΦT t = Φ† t where Φ† is the Moore-Penrose pseudo-inverse of the matrix Φ. 171of 197
- 15. Introduction to Statistical Maximum Likelihood and Least Squares Machine Learning c 2011 Christfried Webers NICTA Found a critical point wML for ln p(t | w, β). Is it a maximum, The Australian National University a minimum, or a saddle point? Calculate the second directional derivative D2 ln p(t | w, β)(ξ, ξ) = −β ξ T ΦT Φξ = −β (Φξ)T Φξ Linear Basis Function Models 2 = −β Φξ ≤0 Maximum Likelihood and Least Squares Geometry of Least We found a maximum. Squares (Is it enough to check the second directional derivative in Sequential Learning two directions ξ which are the same? Yes, because for any Regularized Least Squares bilinear function g(ξ, η), symmetric in its arguments, Multiple Outputs Loss Function for 1 Regression [g(ξ, ξ) + g(η, η) − g(ξ − η, ξ − η)] 2 The Bias-Variance Decomposition 1 = [g(ξ, ξ) + g(η, η) − g(ξ, ξ) − g(η, η) + g(ξ, η) + g(η, ξ)] 2 1 = [g(ξ, η) + g(η, ξ)] = g(ξ, η) 2 172of 197
- 16. Introduction to Statistical Maximum Likelihood and Least Squares Machine Learning c 2011 Christfried Webers NICTA The Australian National The log likelihood is now University ln p(t | wML , β) N N 1 = ln β − ln(2π) − β (t − ΦwML )T (t − ΦwML ) 2 2 2 Linear Basis Function Models Find critical points of ln p(t | w, β) Maximum Likelihood and Least Squares ∂ ln p(t | wML , β) Geometry of Least Squares =0 ∂β Sequential Learning Regularized Least Squares results in Multiple Outputs 1 1 Loss Function for = (t − ΦwML )T (t − ΦwML ) Regression βML N The Bias-Variance Decomposition Note: We can first find the maximum likelihood for w as this does not depend on β. Then we can use wML to find the maximum likelihood solution for β. 173of 197
- 17. Introduction to Statistical Geometry of Least Squares Machine Learning c 2011 Christfried Webers NICTA The Australian National University Target vector t = (t1 , . . . , tN )T ∈ RN Basis vectors ϕj = (Φj1 , . . . , ΦjN )T = (φj (x1 ), . . . , φj (xN ))T ∈ RN span a subspace S Linear Basis Function Find w such that y = (y(x1 , w), . . . , y(xN , w))T ∈ S is closest Models Maximum Likelihood and to t. Least Squares Geometry of Least Squares S Sequential Learning t Regularized Least Squares ϕ2 Multiple Outputs ϕ1 y Loss Function for Regression The Bias-Variance Decomposition 174of 197
- 18. Introduction to Statistical Sequential Learning - Stochastic Gradient Machine Learning c 2011 Descent Christfried Webers NICTA The Australian National University For large data sets, calculating the maximum likelihood parameters wML and βML may be costly. Linear Basis Function For real-time applications, never all data in memory. Models Maximum Likelihood and Use a sequential algorithms (online algorithm). Least Squares Geometry of Least If the error function is a sum over data points E = n En , Squares then Sequential Learning 1 initialise w(0) to some starting value Regularized Least Squares 2 update the parameter vector at iteration τ + 1 by Multiple Outputs (τ +1) (τ ) Loss Function for w =w − η En , Regression The Bias-Variance where En is the error function after presenting the nth data Decomposition set, and η is the learning rate. 175of 197
- 19. Introduction to Statistical Sequential Learning - Stochastic Gradient Machine Learning c 2011 Descent Christfried Webers NICTA The Australian National University For the sum-of-squares error function, stochastic gradient Linear Basis Function Models descent results in Maximum Likelihood and Least Squares (τ +1) (τ ) (τ )T w =w − η tn − w φ(xn ) φ(xn ) Geometry of Least Squares Sequential Learning The value for the learning rate must be chosen carefully. A Regularized Least Squares too large learning rate may prevent the algorithm from Multiple Outputs converging. A too small learning rate does follow the data Loss Function for too slowly. Regression The Bias-Variance Decomposition 176of 197
- 20. Introduction to Statistical Regularized Least Squares Machine Learning c 2011 Christfried Webers NICTA The Australian National University Add regularisation in order to prevent overfitting ED (w) + λEW (w) Linear Basis Function Models with regularisation coefficient λ. Maximum Likelihood and Least Squares Simple quadratic regulariser Geometry of Least Squares 1 T Sequential Learning EW (w) = w w 2 Regularized Least Squares Multiple Outputs Maximum likelihood solution Loss Function for Regression T −1 T w = λI + Φ Φ Φ t The Bias-Variance Decomposition 177of 197
- 21. Introduction to Statistical Regularized Least Squares Machine Learning c 2011 Christfried Webers NICTA The Australian National University More general regulariser M 1 EW (w) = |wj |q 2 Linear Basis Function j=1 Models Maximum Likelihood and q = 1 (lasso) leads to a sparse model if λ large enough. Least Squares Geometry of Least Squares Sequential Learning Regularized Least Squares Multiple Outputs Loss Function for Regression The Bias-Variance Decomposition q = 0.5 q=1 q=2 q=4 178of 197
- 22. Introduction to Statistical Comparison of Quadratic and Lasso Regulariser Machine Learning c 2011 Christfried Webers NICTA The Australian National University Assume a sufficiently large regularisation coefficient λ. Quadratic regulariser Lasso regulariser M M 1 1 Linear Basis Function w2 j |wj | Models 2 2 Maximum Likelihood and j=1 j=1 Least Squares w2 w2 Geometry of Least Squares Sequential Learning Regularized Least Squares Multiple Outputs Loss Function for Regression w w The Bias-Variance Decomposition w1 w1 179of 197
- 23. Introduction to Statistical Multiple Outputs Machine Learning c 2011 Christfried Webers NICTA The Australian National University More than 1 target variable per data point. y becomes a vector instead of a scalar. Each dimension can be treated with a different set of basis functions (and that may be necessary if the data in the different target Linear Basis Function Models dimensions represent very different types of information.) Maximum Likelihood and Least Squares Here we restrict ourselves to the SAME basis functions Geometry of Least Squares y(x, w) = WT φ(x) Sequential Learning Regularized Least Squares where y is a K-dimensional column vector, WT is an M × K Multiple Outputs matrix of model parameters, and Loss Function for φ(x) = (φ0 (x), . . . , φM−1 (x), φ0 (x) = 1, as before. Regression The Bias-Variance Define target matrix T containing the target vector tT in the n Decomposition nth row. 180of 197
- 24. Introduction to Statistical Multiple Outputs Machine Learning c 2011 Christfried Webers NICTA The Australian National University Suppose the conditional distribution of the target vector is an isotropic Gaussian of the form Linear Basis Function p(t | x, W, β) = N (t | WT φ(x), β −1 I). Models Maximum Likelihood and Least Squares The log likelihood is then Geometry of Least Squares N Sequential Learning ln p(T | X, W, β) = ln N (tn | WT φ(xn ), β −1 VI) Regularized Least Squares n=1 Multiple Outputs N NK β β T 2 Loss Function for = ln − tn − W φ(xn ) Regression 2 2π 2 n=1 The Bias-Variance Decomposition 181of 197
- 25. Introduction to Statistical Multiple Outputs Machine Learning c 2011 Christfried Webers NICTA The Australian National University Maximisation with respect to W results in WML = (ΦT Φ)−1 ΦT T. For each target variable tk , we get Linear Basis Function Models Maximum Likelihood and wk = (ΦT Φ)−1 ΦT tk = Φ† tk . Least Squares Geometry of Least Squares The solution between the different target variables Sequential Learning decouples. Regularized Least Squares Holds also for a general Gaussian noise distribution with Multiple Outputs arbitrary covariance matrix. Loss Function for Regression Why? W defines the mean of the Gaussian noise The Bias-Variance distribution. And the maximum likelihood solution for the Decomposition mean of a multivariate Gaussian is independent of the covariance. 182of 197
- 26. Introduction to Statistical Loss Function for Regression Machine Learning c 2011 Christfried Webers NICTA The Australian National University Over-fitting results from a large number of basis functions Linear Basis Function Models and a relatively small training set. Maximum Likelihood and Least Squares Regularisation can prevent overfitting, but how to find the Geometry of Least correct value for the regularisation constant λ ? Squares Sequential Learning Frequentists viewpoint of the model complexity is the Regularized Least bias-variance trade-off. Squares Multiple Outputs Loss Function for Regression The Bias-Variance Decomposition 183of 197
- 27. Introduction to Statistical Loss Function for Regression Machine Learning c 2011 Christfried Webers NICTA The Australian National University Choose an estimator y(x) to estimate the target value t for each input x. Choose a loss function L(t, y(x)) which measures the difference between the target t and the estimate y(x). Linear Basis Function The expected loss is then Models Maximum Likelihood and Least Squares E [L] = L(t, y(x)) p(x, t) dx dt Geometry of Least Squares Sequential Learning Common choice: Squared Loss Regularized Least Squares 2 L(t, y(x)) = {y(x) − t} . Multiple Outputs Loss Function for Regression Expected loss for squared loss function The Bias-Variance Decomposition 2 E [L] = {y(x) − t} p(x, t) dx dt. 184of 197
- 28. Introduction to Statistical Loss Function for Regression Machine Learning c 2011 Christfried Webers NICTA The Australian National University Expected loss for squared loss function Linear Basis Function 2 Models E [L] = {y(x) − t} p(x, t) dx dt. Maximum Likelihood and Least Squares Minimise E [L] by choosing the regression function Geometry of Least Squares Sequential Learning t p(x, t) dt Regularized Least y(x) = = t p(t | x) dt = Et [t | x] Squares p(x) Multiple Outputs Loss Function for (use calculus of variations to derive this result). Regression The Bias-Variance Decomposition 185of 197
- 29. Introduction to Statistical Loss Function for Regression Machine Learning c 2011 Christfried Webers NICTA The Australian National University The regression function which minimises the expected squared loss, is given by the mean of the conditional distribution p(t | x). Linear Basis Function Models t Maximum Likelihood and Least Squares y(x) Geometry of Least Squares Sequential Learning y(x0 ) Regularized Least p(t|x0 ) Squares Multiple Outputs Loss Function for Regression The Bias-Variance x0 x Decomposition 186of 197
- 30. Introduction to Statistical Loss Function for Regression Machine Learning c 2011 Christfried Webers NICTA The Australian National University Analyse the expected loss 2 E [L] = {y(x) − t} p(x, t) dx dt. Linear Basis Function Models Rewrite the squared loss Maximum Likelihood and Least Squares 2 2 {y(x) − t} = {y(x) − E [t | x] + E [t | x] − t} Geometry of Least Squares 2 2 = {y(x) − E [t | x]} + {E [t | x] − t} Sequential Learning Regularized Least + 2 {y(x) − E [t | x]} {E [t | x] − t} Squares Multiple Outputs Claim Loss Function for Regression The Bias-Variance {y(x) − E [t | x]} {E [t | x] − t} p(x, t) dx dt = 0. Decomposition 187of 197
- 31. Introduction to Statistical Loss Function for Regression Machine Learning c 2011 Christfried Webers NICTA The Australian National University Claim {y(x) − E [t | x]} {E [t | x] − t} p(x, t) dx dt = 0. Seperate functions depending on t from function Linear Basis Function Models depending on x Maximum Likelihood and Least Squares Geometry of Least {y(x) − E [t | x]} {E [t | x] − t} p(x, t) dt dx Squares Sequential Learning Regularized Least Calculate the integral over t Squares Multiple Outputs t p(x, t) Loss Function for {E [t | x] − t} p(x, t) dt = E [t | x] p(x) − p(x) dt Regression p(x) The Bias-Variance Decomposition = E [t | x] p(x) − p(x)E [t | x] =0 188of 197
- 32. Introduction to Statistical Loss Function for Regression Machine Learning c 2011 Christfried Webers NICTA The Australian National University The expected loss is now Linear Basis Function Models 2 E [L] = {y(x) − E [t | x]} p(x) dx + var[t | x] p(x) dx Maximum Likelihood and Least Squares Geometry of Least Squares Minimise first term by choosing appropriate y(x). Sequential Learning Second term represents the intrinsic variability of the Regularized Least Squares target data (can be regarded as noise). Independent of the Multiple Outputs choice y(x), can not be reduced by learning a better y(x). Loss Function for Regression The Bias-Variance Decomposition 189of 197
- 33. Introduction to Statistical The Bias-Variance Decomposition Machine Learning c 2011 Christfried Webers NICTA The Australian National University Consider now the dependency on the data set D. Prediction function now y(x; D). Consider again squared loss for which the optimal Linear Basis Function Models prediction is given by the conditional expectation h(x) Maximum Likelihood and Least Squares Geometry of Least h(x) = E [t | x] = t p(t | x) dt. Squares Sequential Learning Regularized Least BUT: we can not know h(x) exactly, as we would need an Squares infinite number of training data to learn it accurately. Multiple Outputs Loss Function for Evaluate performance of algorithm by taking the Regression expectation ED [L] over all data sets D The Bias-Variance Decomposition 190of 197
- 34. Introduction to Statistical The Bias-Variance Decomposition Machine Learning c 2011 Christfried Webers NICTA The Australian National University Taking the expectation over all data sets D ED [E [L]] = ED {y(x; D) − h(x)}2 p(x) dx Linear Basis Function Models + {h(x) − t}2 p(x, t) dx dt Maximum Likelihood and Least Squares Geometry of Least Squares Again, add and subtract the expectation ED [y(x; D)] Sequential Learning Regularized Least {y(x; D) − h(x)}2 = { y(x; D) − ED [y(x; D)] Squares Multiple Outputs + ED [y(x; D)] − h(x)}2 Loss Function for Regression and show that the mixed term does vanish under the The Bias-Variance Decomposition expectation ED [. . .]. 191of 197
- 35. Introduction to Statistical The Bias-Variance Decomposition Machine Learning c 2011 Christfried Webers NICTA The Australian National University Expected loss ED [L] over all data sets D expected loss = (bias)2 + variance + noise. where Linear Basis Function Models 2 (bias)2 = {ED [y(x; D)] − h(x)} p(x) dx Maximum Likelihood and Least Squares Geometry of Least Squares 2 variance = ED {y(x; D) − ED [y(x; D)]} p(x) dx Sequential Learning Regularized Least Squares noise = {h(x) − t}2 p(x, t) dx dt. Multiple Outputs Loss Function for Regression squared bias : how much does the average prediction over The Bias-Variance all data sets differ from the desired regression function ? Decomposition variance : how much do solutions for individual data sets vary around their average ? 192of 197
- 36. Introduction to Statistical The Bias-Variance Decomposition Machine Learning c 2011 Christfried Webers NICTA The Australian National University Dependence of bias and variance on the model complexity Linear Basis Function Models 1 1 ln λ = 2.6 Maximum Likelihood and t t Least Squares 0 0 Geometry of Least Squares Sequential Learning −1 −1 Regularized Least Squares 0 1 0 1 Multiple Outputs x x Loss Function for Left: Result of fitting the model to 100 data sets, only 25 shown. Regression Right: Average of the 100 fits in red, the sinusoidal function The Bias-Variance Decomposition from where the data were created in green. 193of 197
- 37. Introduction to Statistical The Bias-Variance Decomposition Machine Learning c 2011 Christfried Webers NICTA The Australian National University Dependence of bias and variance on the model complexity Linear Basis Function Models 1 1 ln λ = −0.31 t t Maximum Likelihood and Least Squares 0 0 Geometry of Least Squares Sequential Learning −1 −1 Regularized Least Squares 0 1 0 1 Multiple Outputs x x Loss Function for Left: Result of fitting the model to 100 data sets, only 25 shown. Regression Right: Average of the 100 fits in red, the sinusoidal function The Bias-Variance Decomposition from where the data were created in green. 194of 197
- 38. Introduction to Statistical The Bias-Variance Decomposition Machine Learning c 2011 Christfried Webers NICTA The Australian National University Dependence of bias and variance on the model complexity Linear Basis Function Models 1 1 ln λ = −2.4 t t Maximum Likelihood and Least Squares 0 0 Geometry of Least Squares Sequential Learning −1 −1 Regularized Least Squares 0 1 0 1 Multiple Outputs x x Loss Function for Left: Result of fitting the model to 100 data sets, only 25 shown. Regression Right: Average of the 100 fits in red, the sinusoidal function The Bias-Variance Decomposition from where the data were created in green. 195of 197
- 39. Introduction to Statistical The Bias-Variance Decomposition Machine Learning c 2011 Christfried Webers NICTA The Australian National Squared bias, variance, their sum, and test data University The minimum for (bias)2 + variance occurs close to the value that gives the minimum error 0.15 Linear Basis Function Models (bias)2 Maximum Likelihood and 0.12 variance Least Squares (bias)2 + variance Geometry of Least Squares 0.09 test error Sequential Learning Regularized Least 0.06 Squares Multiple Outputs 0.03 Loss Function for Regression The Bias-Variance 0 Decomposition −3 −2 −1 0 1 2 ln λ 196of 197
- 40. Introduction to Statistical The Bias-Variance Decomposition Machine Learning c 2011 Christfried Webers NICTA The Australian National University Tradeoff between bias and variance Linear Basis Function Models simple models have high bias and low variance Maximum Likelihood and complex models have low bias and high variance Least Squares The sum of bias and variance has a minimum at some Geometry of Least Squares model complexity. Sequential Learning The bias-variance decomposition needs many data sets, Regularized Least Squares which are not always available. Multiple Outputs Loss Function for Regression The Bias-Variance Decomposition 197of 197