Machine Learning Notes for beginners ,Step by step
- 1. INDIAN INSTITUTE OF TECHNOLOGY ROORKEE [email protected] https://faculty.iitr.ac.in/cs/bala/ CSN-382 (Lecture 10) Dr. R. Balasubramanian Professor Department of Computer Science and Engineering Mehta Family School of Data Science and Artificial Intelligence Indian Institute of Technology Roorkee Roorkee 247 667 Machine Learning
- 2. 2 ● Signal – all valid values for a variable (shows between max and min values for x axis and y axis). Represents a valid data. ● Noise – The spread of data points across the best fit line. For a given value of x, there are multiple values of y (some on line and some around the line). This spread is due to random factors. ● Signal to Noise Ratio – Variance of signal / variance in noise. ● Greater the SNR the better the model will be. X min X max Signal Y max Y min + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + PCA (Signal to noise ratio)
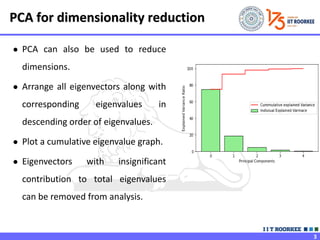
- 3. 3 ● PCA can also be used to reduce dimensions. ● Arrange all eigenvectors along with corresponding eigenvalues in descending order of eigenvalues. ● Plot a cumulative eigenvalue graph. ● Eigenvectors with insignificant contribution to total eigenvalues can be removed from analysis. PCA for dimensionality reduction
- 4. 4 Advantages Disadvantages ● Helps is reducing dimensions ● Correlated features are removed ● Improves performance of an algorithm ● Low noise sensitivity ● Assumes that feature set is correlated ● Sensitive to outliers ● High variance axis is treated as PC, and low variance axes are treated as noise ● Covariance matrix are difficult to be evaluated in an accurate manner Advantages and disadvantages
- 5. 5 ● Dimensionality reduction ● Improving signal to noise ratio ● Helps in removing correlation between variables ● To speed up the convergence of Neural networks ● Computer vision (Face recognition) Applications of PCA
- 6. 6 Feature Selection ► Instance based learning (kNN, last class) Not useful if the number of features is large. ► Feature Reduction Features contain information about the target. ► More features means better information or more information, and better discriminative power or better classification power. But this may not be true always
- 8. 8 Curse of Dimensionality ► Irrelevant features In algorithm such as k nearest neighbor these irrelevant features introduce noise and they fool the learning algorithm. ► Redundant features If you have a fixed number of training examples and redundant features which do not contribute additional information they may lead to degradation in performance of the learning algorithm. ► These irrelevant features and redundant features can confuse learner, especially when you have limited training examples and limited computational resources. ► Large number of features and limited training examples Overfitting
- 9. 9 To overcome Curse of Dimensionality ► Feature Selection ► Feature Extraction
- 10. 10 Feature Selection ► Given Set of initial features 𝐹 = {𝑥1, 𝑥2, 𝑥3, … , 𝑥𝑛} ► we can find 𝐹′ = {𝑥1′, 𝑥2′, 𝑥3′, … , 𝑥𝑚′}⊂ 𝐹 ► We want to find a subset 𝐹′ of those features in 𝐹 so that it optimizes certain criteria. ► How feature selection is differing from feature extraction. ► Feature selection in problems like hyperspectral imaging. ► From 𝑛 features set, we can have 2𝑛 possible feature subsets. Optimized algorithm in polynomial time Heuristic Greedy algorithm Randomized algorithm
- 11. 11 Feature Subset Evaluation ► Unsupervised (Filter method) ► Supervised (Wrapper method)
- 12. 12 Feature Selection Steps ► Feature Selection is an optimization problem: ► Step 1: Search the space of possible feature subsets. ► Step 2: Pick the subset that is optimal or near optimal w.r.t some optimal function.
- 13. 13 Feature Selection Steps ► Search Strategies Optimum Heuristic Randomized ► Evaluation Methods Filter methods Wrapper methods
- 14. 14 Evaluating Feature Subset ► Supervised (Wrapper method) Train using selected subset Estimate error on validation dataset ► Unsupervised (Filter method) Look at input only Select the subset that has most input
- 16. 16 Two different frameworks of feature selection ► Find uncorrelated features in the reduced features ► Heuristic algorithms Forward Selection Algorithm Backward Selection Algorithm ► Forward Selection Algorithm Start with empty feature set and then you add features one by one ► Backward Selection Algorithm In backward search you start with the full feature set. Then you try removing features from the features that you have.
- 17. 17 Feature Selection ► Univariate (looks at each feature independently of others) Pearson correlation coefficient F-Score Chi-Square Signal to noise ratio ► Rank features by importance ► Ranking cut-off determined by user ► Univariate methods measure some type of correlation between two random variables. ► The label 𝑦𝑖 and a fixed feature, 𝑥𝑖𝑗 for fixed 𝑗
- 18. 18 Pearson correlation coefficient ► Please refer lecture 4 slides
- 19. 19 ● Signal – all valid values for a variable (shows between max and min values for x axis and y axis). Represents a valid data. ● Noise – The spread of data points across the best fit line. For a given value of x, there are multiple values of y (some on line and some around the line). This spread is due to random factors. ● Signal to Noise Ratio – Variance of signal / variance in noise. ● Greater the SNR the better the model will be. X min X max Signal Y max Y min + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + Signal to noise ratio
- 20. 20 Multivariate Feature Selection ► Multivariate (consider all features simultaneously). ► Consider the vector 𝑤 for any linear classifier. ► Classification of point 𝑥 is given by 𝑤𝑇𝑥 + 𝑤0. ► Small entries of 𝑤 will have little effect on dot product and hence those features are less relevant. ► For example if 𝑤 = (10, 0.01, −9) then features 0 and 2 are contributing more to a dot product than feature 1. A ranking of features given by this 𝑤 are 0,2 and 1. ► The 𝑤 can be obtained any of linear classifiers.
- 21. 21 Multivariate Feature Selection ► A variant of this approach is called recursive feature elimination Compute 𝑤 on all features Remove features with smallest 𝑤𝑖 Precompute 𝑤 on reduced data Goto step 2 if stopping criteria doesn’t meet.
- 23. 23 ● Linear Discriminant Analysis is a supervised learning algorithm for classification. ● Similar to PCA, it can be used for dimensionality reduction, by projecting the input data to a linear subspace consisting of the directions which maximize the separation between classes. ● It is a linear transformation technique. ● It can be used as a pre-processing stage for pattern-classification. ● The purpose of LDA is to lower the dimension space with a good separability between the classes. ● It assumes that the features are normally distributed. Linear Discriminant Analysis
- 25. 25 ● Fisher’s LDA aims to maximise equation (1), maximize the distance between means and minimize the variance within classes ● Equation-1 can be rewritten with two new terms: ○ Between class matrix (SB) ○ Within class matrix (SW) Here, W is a unit vector onto which the data points are to be projected. Objective of LDA
- 26. 26 ● Upon differentiating the equation (2) w.r.t W and equating with 0, we get a generalized eigenvalue- eigenvector problem ○ SBW = vSwW ○ Sw -1SBW = vW ■ Where v = eigenvalue ■ W = eigenvector Objective of LDA
- 27. 27 LDA Matrix ● SB represents how precisely the data is scattered across the classes ● Goal is to maximize SB. i.e. the distance between the two classes should be higher Between Class Matrix(SB) Step:2 ● SW captures how precisely the data is scattered within the class ● Goal is to minimize SW. i.e. the distance between the elements of the class should be minimum Within Class Matrix(SW) LDA Matrix
- 28. 28 Linear Discriminant Analysis - Procedure
- 29. 29 Thank You!