Minimum Spanning Tree (MST), Kruskal's algorithm and Prim's Algorithm, and their Java codes

Minimum Spanning Tree (MST) - Kruskal’s algorithm
and Prim’s algorithm, and their Java codes
by
Dr.Animesh Chaturvedi
Assistant Professor: LNMIIT Jaipur
Post Doctorate: King’s College London &TheAlanTuring Institute
PhD: IIT Indore

Adjacency Matrix Representation of Graph

Adjacency List Representation of Graph

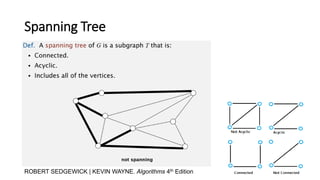
Spanning Tree
• A tree T is said to be a spanning tree of a
connected graph G, if T is a subgraph of G and T
contains all vertices of G.
• A graph G is said to be connected if there is at least
one path between every pair of vertices in G.
Otherwise, G is disconnected.
• A disconnected graph with k components has a
spanning forest consist of k spanning trees.
• All spanning trees have exactly |V| - 1 edges.

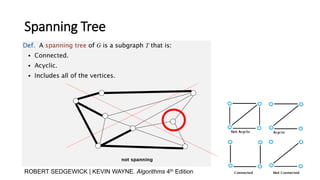
Spanning Tree
ROBERT SEDGEWICK | KEVIN WAYNE. Algorithms 4th Edition

Spanning Tree Properties
• Every connected graph has at least one spanning tree.
• An edge in a spanning tree T is called a branch of T.
• A pendant edge in a graph G is contained in every spanning tree of G.

Spanning tree and Cut set
• In a connected graph G, a cut-set is a set of edges whose removal
from G leaves G disconnected, provided removal of no proper subset
of these edges disconnects G.
• Same is a true for a Spanning Tree as it is also a connected graph

Spanning tree and Cut set
• Every cut-set in a connected graph G must contain
atleast one branch of every spanning tree of G, the
converse is also true.
• In a connected graph G, any minimal set of edges
containing at least one branch of every spanning
tree of G is a cut-set.

Design of Electronic circuitry
• In the Design of Electronic circuitry,
pins of several components electrically equivalent
by wiring them together.
• To interconnect a set of n pins,
• we can use an arrangement of n - 1 wires,
• each connecting two pins
• The one that uses the least amount of wire is usually the most
desirable.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms (Vol. 3,
pp. 624-642). Cambridge: MIT press.

Design of Electronic circuitry
Model this wiring problem with a connected,
undirected graph G = (V, E),
where V is the set of pins, E is the set of possible interconnections
between pairs of pins.
Find an acyclic subset that connects all the vertices and whose total
weight is minimized the cost (amount of wire needed).
This forms a tree T as a acyclic and connects all of the vertices, which
we call the minimum-spanning-tree

Minimum Spanning Tree
• “minimum spanning tree” is a shortened form of the phrase
“minimum-weight spanning tree.”
• Minimizing the number of edges in T,
• Graph is connected and Edge weights are distinct. Then, MST exists
and is unique.
• All spanning trees have exactly
|V| - 1 edges

• The weights on edges and the edges in a minimum spanning tree are
shaded. The total weight of the tree is 37.
• This minimum spanning tree is not unique: removing the edge (b, c)
and replacing it with the edge (a, h ) yields another spanning tree
with weight 37.

Minimum Spanning Tree and Cut-sets
• A cut in a graph is a partition of its vertices
into two (nonempty) sets.
• A crossing edge connects a vertex in one set
with a vertex in the other.
• Cut property. Given any cut, the crossing
edge of min weight is in the MST.

Minimum Spanning Tree and Cut-sets
• Suppose min-weight crossing edge e is not in the MST.
• Adding e to the MST creates a cycle.
• Some other edge f in cycle must be a crossing edge.
• Removing f and adding e is also a spanning tree.
• Since weight of e is less than the weight of f, that spanning tree is
lower weight.
• Contradiction

GENERIC-MST
• Safe edge for A, since it can be safely added to A while maintaining
the invariant (MST do not form loop or cycle).
• Initialization: line 1 the set A trivially satisfies the invariant.
• Maintenance: The loop in lines 2-4 maintains the invariant by adding
only safe edges
• Termination: All edges (|V|-1) added to A are in a MST, and so the
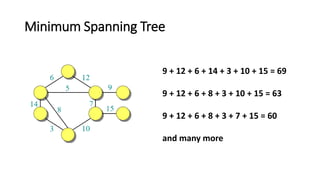
set A is returned in line 5 must be a minimum spanning tree.

9 + 12 + 6 + 14 + 3 + 10 + 15 = 69
9 + 12 + 6 + 8 + 3 + 10 + 15 = 63
9 + 12 + 6 + 8 + 3 + 7 + 15 = 60
and many more

9 + 5 + 6 + 8 + 3 + 7 + 15 = 53

24 + 4 + 6 + 8 + 10 + 11 + 7 = 70
9 + 4 + 6 + 8 + 10 + 11 + 7 = 55
and many more

Minimum Spanning Tree Applications
• Cluster analysis.
• Max bottleneck paths.
• Real-time face verification.
• Find road networks in satellite and aerial imagery.
• Reducing data storage in sequencing amino acids in a protein.
• Model locality of particle interactions in turbulent fluid flows.
• Autoconfig protocol for Ethernet bridging to avoid cycles in a network.
• Approximation algorithms for NP-hard problems (e.g., TSP).
• Network design (communication, electrical, hydraulic, computer, road).

Kruskal’s algorithm and Prim’s algorithm

• Two algorithms for solving the minimum spanning-tree problem:
• Kruskal’s algorithm
• Prim’s algorithm
• The two algorithms are
• greedy algorithms

• At each step of an algorithm, one of several possible choices. Then,
• Greedy strategy: make the choice that is the best at the moment
• Not generally guaranteed to find globally optimal solutions to
problems.
• Certain greedy do yield a spanning tree with minimum weight.

• An edge is a light edge crossing a cut if its weight is the minimum of
any edge crossing the cut.
• Light edge = minimum-weight crossing edge
• Light edge satisfy MST properties, and its weight is the minimum of
any other edges satisfying the MST properties.
• more than one light edge crossing a cut in the case of ties.

Kruskal’s algorithm
• Both Kruskal’s algorithm and Prim’s algorithm elaborate the
generic algorithm because they uses a specific rule to determine a
safe edge in line 3 of GENERIC-MST.
• In Kruskal’s algorithm,
• the set A is a forest.
• the safe edge added to A is always a least-weight edge in the graph that
connects two distinct components.
• Greedy algorithm because it adds an edge of least possible weight to
the forest.

• In Kruskal’s algorithm,
• the set A is a forest.
• the safe edge added to A is always a least-weight edge in the graph that
connects two distinct components.
• A tree is a connected, acyclic, undirected graph.
• A forest is a set of trees (non necessarily connected)

• Shaded edges belong to the
forest A being grown.
• The edges are considered by
the algorithm in sorted order
by weight.
• An arrow points to the edge
under consideration at each
step of the algorithm.
• If the edge joins two distinct
trees in the forest, it is added
to the forest, thereby
merging the two trees.

• It uses a disjoint-set data structure to maintain several disjoint sets of
elements.
• A disjoint-set data structure keeps track of a set of elements
partitioned into a number of disjoint (non-overlapping) subsets.
• A union-find data structure performs three useful operations
• Making a new set containing a new element.
• Find: Determine which subset a particular element. This can be used
for determining whether two elements are in the same subset.
• Union: Join two subsets into a single set.
https://en.wikipedia.org/wiki/Disjoint-set_data_structure

• Each set contains the vertices in a tree of the current forest. The
operation FIND-SET(u) returns a representative element from the set
that contains u.
• Thus, we can determine whether two vertices u and v belong to the
same tree by testing whether FIND-SET(u) equals FIND-SET(v).
• The combining of trees is accomplished by the UNION procedure.

• Lines 1-3: initialize the set A to the empty set and create trees, one
containing each vertex.
• Line 4: The edges in E are sorted into non-decreasing order by weight.

• The for loop in lines 5-8 checks, for each edge (u, v), whether the
endpoints u and v belong to the same tree.
• If they do, then the edge (u, v) cannot be added to the forest because it
create a cycle, thus the edge is discarded.
• Otherwise, the two vertices belong to different trees.
• In this case, the edge (u, v ) is added to A in line 7, and the vertices in
the two trees are merged in line 8.

• Running time depends on
the implementation of
the disjoint set data structure
• the set A in line 1 takes O(1) time,
• MAKE-SET operations in the for loop of lines 2–3 takes O(V),
• the time to sort the edges in line 4 is O(E lg E),
• the for loop of lines 5–8 performs O(E) FIND-SET and UNION operations on
the disjoint-set forest.
• Observing that |E| < |V|2, we have lg|E| = O(lg V), and so we can restate
the running time of Kruskal’s algorithm as O(E lg V).

Prim’s algorithm
• Both Kruskal’s algorithm and Prim’s algorithm elaborate the generic
algorithm because they uses a specific rule to determine a safe edge
in line 3 of GENERIC-MST.
• In Prim’s algorithm,
• the set A forms a single tree.
• the safe edge added to A is always a least-weight edge connecting the tree to
a vertex not in the tree.
• Greedy algorithm because the tree is augmented at each step with an
edge that contributes the minimum amount possible to the tree’s
weight.

Prim’s Algorithm
• Prim’s algorithm operates much like Dijkstra’s algorithm for finding
shortest paths in a graph.
• The edges in the set A always form a single tree.
• The tree starts from an arbitrary vertex and grows until the tree spans
all the vertices in V.
• At each step, a light edge is added to the tree A, that connects A to an
isolated vertex.

Prim’s Algorithm
• The root vertex is a. Shaded edges
are in the tree being grown, and
the vertices in the tree are shown
in black.
• The vertices in the tree determine
a cut of the graph, and a light edge
crossing
the cut is added to the tree.
• the algorithm has a choice of
adding either edge (b, c) or edge (a,
h) to the tree since both are light
edges crossing the cut.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to Algorithms (Vol. 3, pp. 624-642). Cambridge: MIT press.

Prim’s Algorithm
Lines 1-5 set the key of each vertex to ∞ (except for the root r, whose
key is set to 0 so that it will be the first vertex processed).
Set the parent of each vertex to NIL, and initialize the min-priority
queue Q to contain all the vertices.
• v.key is the minimum weight of any edge
connecting v to a vertex in the tree
• v.∏ is the names the parent of v in the tree
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009).
Introduction to Algorithms (Vol. 3, pp. 624-642). Cambridge: MIT press.

Prim’s Algorithm

Prim’s Algorithm
The for loop of lines 8-11 update the key and ∏ fields of every vertex v
adjacent to u but not in the tree. The updating maintains the third part
of the loop invariant.

Prim’s Algorithm
• the BUILD-MIN-HEAP procedure to perform lines
1–5 in O(V) time.
• while loop executes |V| times, and each EXTRACT-
MIN operation takes O(lg V) time, the total time is
O(V lg V).
• The for loop in lines 8–11 executes O(E) times, and
line 11 involves in O(lg V) time, the total time is
O(E lg V).
• The total time is O(V lg V + E lg V) = O(E lg V),
which is asymptotically the same as for Kruskal’s
algorithm.
• The running time of Prim’s algorithm depends on how min-priority
queue Q is implemented. Implement Q as a binary min-heap,

Prim’s Algorithm
• while loop executes |V| times, and each
EXTRACT-MIN operation takes O(lg V), the
total time is O(V lg V).
• The for loop in lines 8–11 executes O(E)
times, and line 11 takes O(1), the total time
is O(E).
• the running time of Prim’s algorithm
improves to O(E + V lg V).
• The running time of Prim’s algorithm depends on how min-priority
queue Q is implemented. Implement Q as a Fibonacci heap,

Minimum Spanning Tree (MST), Kruskal's algorithm and Prim's Algorithm, and their Java codes

Applications

Java code Implementation of

Java Implementation

Java Implementation – Kruskal’s Algorithm
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction
to Algorithms (Vol. 3, pp. 624-642). Cambridge: MIT press.

Java Implementation – Prim’s Algorithm
Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction
to Algorithms (Vol. 3, pp. 624-642). Cambridge: MIT press.

Thank You
Japanese
Hebrew
English
Merci
French
Russian
Danke
German
Grazie
Italian
Gracias
Spanish
Obrigado
Portuguese
Arabic
Simplified
Chinese
Traditional
Chinese
Tamil
Thai
Korean
https://sites.google.com/site/animeshchaturvedi07

Minimum Spanning Tree (MST), Kruskal's algorithm and Prim's Algorithm, and their Java codes

More Related Content

What's hot (20)

Similar to Minimum Spanning Tree (MST), Kruskal's algorithm and Prim's Algorithm, and their Java codes (20)

More from Animesh Chaturvedi (20)

Recently uploaded (20)

Minimum Spanning Tree (MST), Kruskal's algorithm and Prim's Algorithm, and their Java codes