![ F(x) = [F1(x), F2(x),...,Fm(x)],
Min F(x), subject to Gi(x)=0, i=1,...,ke; Gi(x)≤0, i=ke+1,...,k; l≤x≤u.
Simple car design example: two objectives - cost and accident rate –
both of which are to be minimized.
7
MOOP MATHS
A, B, D - One objective
can only be improved at
the expense of at least
one other objective!](https://image.slidesharecdn.com/multiobjectiveoptimizationandparetomultiobjectiveoptimizationwithcasestudy-190402034906/85/Multi-Objective-Optimization-and-Pareto-Multi-Objective-Optimization-with-case-study-7-320.jpg)
![ STEPS
1. Define Rosen brock function in editor…….. save
2. Define constraint in other editor window……..save
Here, use [ ] blank to add equality
3. Use optimization app>>>>fmincon-constrained nonlinear minimization
4. Give objective function, starting point, constraint function
START………………
FIND FINAL POINT WITH MINIMUM OB. FUNCTION
19
MOOP IN MATLAB (ROSEN BROCK FUNCTION)](https://image.slidesharecdn.com/multiobjectiveoptimizationandparetomultiobjectiveoptimizationwithcasestudy-190402034906/85/Multi-Objective-Optimization-and-Pareto-Multi-Objective-Optimization-with-case-study-19-320.jpg)
Multi Objective Optimization and Pareto Multi Objective Optimization with case study
- 1. CHAPTER-5 MULTI OBJECTIVE OPTIMIZATION AND PARETO MULTI OBJECTIVE OPTIMIZATION OPTIMIZATION TECHNIQUES AND OPERATIONS RESEARCH PRESENTED BY: ADITYA DESHPANDE (S-42) GUIDED BY: PROF. G. N. KOTWAL SIR
- 2. Involve more than one objective function that are to be minimized or maximized Answer is set of solutions that define the best trade off between competing objectives Basic difference is in the single-objective optimization problem, the superiority of a solution over other solutions easily determined by comparing their objective function values. 2 CONCEPT OF MOOP
- 3. In multi-objective optimization problem, the goodness of a solution is determined by the dominance Real-world problems have more than one objective function, each of which may have a different individual optimal solution. Different in the optimal solutions corresponding to different objectives because the objective functions are often conflicting (competing) to each other. Set of trade-off optimal solutions instead of one optimal solution, generally known as “Pareto-Optimal” solutions (named after Italian economist Vilfredo Pareto (1906)). No one solution can be considered to be better than any other with respect to all objective functions. The non-dominant solution concept. 3 CONCEPT OF MOOP(cont…)
- 5. Other example fields: 1. Economics 2. Optimal control and design 3. Process optimization 4. Radio resource management 5. Electric power systems 5 MOOP EXAMPLES
- 6. Non-dominated - given two objectives, a non-dominated solution is when none of both solution are better than the other with respect to two objectives. Both objectives are equally important. e.g. speed and price. Dominated: when solution a is no worse than b in all objectives, and solution a is strictly better than b in at least one objective, then solution a dominate solution b. 6 Non Dominated & Dominated Solutions
- 7. F(x) = [F1(x), F2(x),...,Fm(x)], Min F(x), subject to Gi(x)=0, i=1,...,ke; Gi(x)≤0, i=ke+1,...,k; l≤x≤u. Simple car design example: two objectives - cost and accident rate – both of which are to be minimized. 7 MOOP MATHS A, B, D - One objective can only be improved at the expense of at least one other objective!
- 8. Need to save money Or Have shortest flying time If we compare tickets A & B, we can’t say that either is superior without knowing the relative importance of Travel Time vs. Price. comparing tickets B & C shows that C is better than B in both objectives, so we can say that C “dominates” B. as long as C is a feasible option, there is no reason we would choose B. 8 Ticket Travel Time (hrs) Ticket Price (Rs) A 10 17000 B 9 20000 C 8 18000 D 7.5 23000 E 6 22000 Flying Example
- 9. D is dominated by E rest of the options (A, C, & E) have a trade-off associated with Time vs. Price, so none is clearly superior to the others 9 Flying Example Plane Ticket Options 0 1000 2000 3000 4000 5000 0 5 10 15 20 25 Flight Time (hrs) Price($) AE D C B Feasible Region
- 10. Solutions that lie along the line are non-dominated solutions those lie inside the line are dominated because there is always another solution on the line that has at least one objective that is better. The line is called- Pareto front and solutions on it are Pareto-optimal. All Pareto-optimal solutions are non-dominated. Imp to find the solutions as close as possible to the Pareto front & as far along it as possible. 10 f1 f2 Feasible RegionPareto Front
- 11. 1. Traditional Approach A.Aggregating approaches i. Weighting Method ii. Constraint Method iii.Goal Programming iv.Minmax Approach B. VEGA (Vector Evaluated Genetic Algorithm) 2. Pareto Techniques B. Genetic Algorithm (GA) C. Multi-Objective Evolutionary Algorithm (MOEA) 11 Two approaches for MOOP
- 12. 12 RESPONSE SURFACE OPTIMIZATION MOOP IN ANSYS
- 13. 13 MOOP IN ANSYS
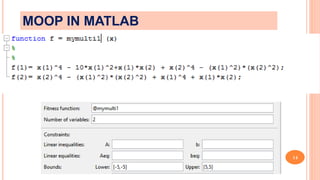
- 15. 15 The gamultiobj solver attempts to create a set of Pareto optima for a multiobjective minimization. You may optionally set bounds or other constraints on variables. gamultiobjuses the genetic algorithm for finding local Pareto optima. As in the ga function, you may specify an initial population, or have the solver generate one automatically. Multiobjective optimization is, therefore, concerned with the generation and selection of noninferior solution points. Noninferior solutions are called Pareto optima. A general goal in multiobjective optimization is constructing the Pareto optima using GAMULTIOBJ MOOP IN MATLAB
- 16. 16
- 17. 17
- 18. The function f(x) is called the objective function. This is the function you wish to minimize The inequality x1 2+x2 2≤1 is called a constraint. Constraints limit the set of x over which you may search for a minimum. Non linear problem only using inequality So need to add equality by ourselves 18 MOOP IN MATLAB (ROSEN BROCK FUNCTION)
- 19. STEPS 1. Define Rosen brock function in editor…….. save 2. Define constraint in other editor window……..save Here, use [ ] blank to add equality 3. Use optimization app>>>>fmincon-constrained nonlinear minimization 4. Give objective function, starting point, constraint function START……………… FIND FINAL POINT WITH MINIMUM OB. FUNCTION 19 MOOP IN MATLAB (ROSEN BROCK FUNCTION)
- 20. THANK YOU20