Neural Network Back Propagation Algorithm
- 1. for recognizing handwritten digits "It's artificial intelligence until you know how it works"
- 2. • Process input to output • How good did the network do? • Train the network to perform better • Use algorithm to recognize digits
- 3. Dot Product 𝑎 𝑏 𝑐 𝑑 ∙ 𝑒 𝑓 𝑔 ℎ = (𝑎 ∙ 𝑒 + 𝑏 ∙ 𝑔) (𝑎 ∙ 𝑓 + 𝑏 ∙ ℎ) (𝑐 ∙ 𝑒 + 𝑑 ∙ 𝑔) (𝑐 ∙ 𝑓 + 𝑑 ∙ ℎ) Multiply by scalar 𝑎 𝑏 𝑐 × 𝑑 = 𝑎 ∙ 𝑑 𝑏 ∙ 𝑑 𝑐 ∙ 𝑑 Pointwise multiply 𝑎 𝑏 𝑐 × 𝑑 𝑒 𝑓 = 𝑎 ∙ 𝑑 𝑏 ∙ 𝑒 𝑐 ∙ 𝑓 Outer Product 𝑎 𝑏 𝑐 ⨂ 𝑑 𝑒 = 𝑎 ∙ 𝑑 𝑎 ∙ 𝑒 𝑏 ∙ 𝑑 𝑐 ∙ 𝑑 𝑏 ∙ 𝑒 𝑐 ∙ 𝑒
- 4. Slope of a function at each point ↓ Shows how sensitive the function is to changes in its parameters f(x)
- 5. Slope of a function at each point ↓ Shows how sensitive the function is to changes in its parameters f’(x) = derivative of f(x) f(x)
- 6. Slope of a function at each point ↓ Shows how sensitive the function is to changes in its parameters f’(x) = derivative of f(x) f(x) f’(x)high f(x)is sensitive to changes in X
- 7. Slope of a function at each point ↓ Shows how sensitive the function is to changes in its parameters f’(x) = derivative of f(x) f(x) f’(x)high f(x)is sensitive to changes in X f’(x)low f(x)is not sensitive to changes in X
- 14. w1 w2 w3 𝑖=1 𝑚 (𝑤𝑖∙ 𝑎𝑖) Sum up the weighted inputbias a1 a2 a3
- 15. w1 w2 w3 𝑖=1 𝑚 (𝑤𝑖∙ 𝑎𝑖) + 𝑏𝑖𝑎𝑠 Sum up the weighted input Add the node’s bias bias a1 a2 a3
- 16. w1 w2 w3 𝑖=1 𝑚 (𝑤𝑖∙ 𝑎𝑖) + 𝑏𝑖𝑎𝑠𝑧 = Sum up the weighted input Add the node’s bias bias a1 a2 a3 Input Sum
- 17. w1 w2 w3 𝑖=1 𝑚 (𝑤𝑖∙ 𝑎𝑖) a = 𝑓(𝑧)+ 𝑏𝑖𝑎𝑠𝑧 = Sum up the weighted input Add the node’s bias Apply activation function bias a1 a2 a3 Input Sum Activation
- 18. w1 w2 w3 𝑖=1 𝑚 (𝑤𝑖∙ 𝑎𝑖) a = 𝑓(𝑧)+ 𝑏𝑖𝑎𝑠𝑧 = Sum up the weighted input Add the node’s bias Apply activation function bias = 0.1 = 0.2 = 0.3 = 0.06 a1 = 0.1 a2 = 0.2 a3 = 0.3 Input Sum Activation
- 19. w1 w2 w3 𝑖=1 𝑚 (𝑤𝑖∙ 𝑎𝑖) a = 𝑓(𝑧)+ 𝑏𝑖𝑎𝑠𝑧 = Sum up the weighted input Add the node’s bias Apply activation function bias = 0.1 = 0.2 = 0.3 = 0.06 a1 = 0.1 a2 = 0.2 a3 = 0.3 𝟎. 𝟏 ∙ 𝟎. 𝟏 𝟎. 𝟐 ∙ 𝟎. 𝟐 𝟎. 𝟑 ∙ 𝟎. 𝟑 ----------- + 0.14 Input Sum Activation
- 20. w1 w2 w3 𝑖=1 𝑚 (𝑤𝑖∙ 𝑎𝑖) a = 𝑓(𝑧)+ 𝑏𝑖𝑎𝑠𝑧 = Sum up the weighted input Add the node’s bias Apply activation function bias = 0.1 = 0.2 = 0.3 = 0.06 a1 = + 0.06 = 0.20 = 0.1 a2 = 0.2 a3 = 0.3 0.14 Input Sum Activation
- 21. w1 w2 w3 𝑖=1 𝑚 (𝑤𝑖∙ 𝑎𝑖) a = 𝑓(𝑧)+ 𝑏𝑖𝑎𝑠𝑧 = Sum up the weighted input Add the node’s bias Apply activation function bias = 0.1 = 0.2 = 0.3 = 0.06 a1 = + 0.06 = 0.20 = 0.1 a2 = 0.2 a3 = 0.3 𝜎 0.20 𝟎. 𝟓𝟒𝟗𝟖 0.14 Input Sum
- 22. 𝜎 𝑧 = 1 1 + 𝑒−𝑧 𝜎′ 𝑧 = 𝜎 𝑧 ∙ (1 − 𝜎 𝑧 ) 𝑧 𝐴ctivation
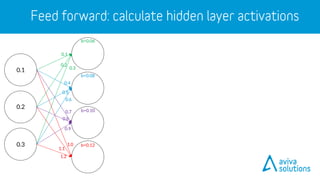
- 26. 0.1 0.2 0.3 1.0 1.1 1.2 0.4 0.5 0.6 0.7 0.8 0.9 b=0.06 b=0.08 b=0.10 b=0.12 𝐳 = 𝑖=1 𝑚 (𝑤𝑖∙ 𝑖𝑛𝑝𝑢𝑡) + 𝑏𝑖𝑎𝑠 0.1 0.2 0.3
- 27. 0.1 0.2 0.3 1.0 1.1 1.2 0.4 0.5 0.6 0.7 0.8 0.9 b=0.06 b=0.08 b=0.10 b=0.12 𝐳 = 𝑖=1 𝑚 (𝑤𝑖∙ 𝑖𝑛𝑝𝑢𝑡) + 𝑏𝑖𝑎𝑠 𝐚 = 𝜎 𝑧 0.1 0.2 0.3
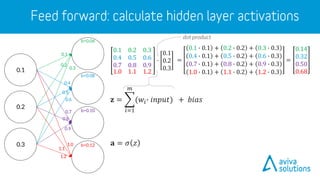
- 28. 0.1 0.2 0.3 1.0 1.1 1.2 0.4 0.5 0.6 0.7 0.8 0.9 0.1 0.4 0.7 0.2 0.5 0.8 0.3 0.6 0.9 1.0 1.1 1.2 b=0.06 b=0.08 b=0.10 b=0.12 𝐳 = 𝑖=1 𝑚 (𝑤𝑖∙ 𝑖𝑛𝑝𝑢𝑡) + 𝑏𝑖𝑎𝑠 𝐚 = 𝜎 𝑧 0.1 0.2 0.3 ∙ 0.1 0.2 0.3
- 29. 0.1 0.2 0.3 1.0 1.1 1.2 0.4 0.5 0.6 0.7 0.8 0.9 0.1 0.4 0.7 0.2 0.5 0.8 0.3 0.6 0.9 1.0 1.1 1.2 dot product b=0.06 b=0.08 b=0.10 b=0.12 𝐳 = 𝑖=1 𝑚 (𝑤𝑖∙ 𝑖𝑛𝑝𝑢𝑡) + 𝑏𝑖𝑎𝑠 𝐚 = 𝜎 𝑧 = 0.1 ∙ 0.1 + 0.2 ∙ 0.2 + 0.3 ∙ 0.3 0.4 ∙ 0.1 + 0.5 ∙ 0.2 + 0.6 ∙ 0.3 0.7 ∙ 0.1 + 0.8 ∙ 0.2 + 0.9 ∙ 0.3 1.0 ∙ 0.1 + 1.1 ∙ 0.2 + 1.2 ∙ 0.3 = 0.14 0.32 0.50 0.680.1 0.2 0.3 ∙ 0.1 0.2 0.3
- 30. 0.1 0.2 0.3 1.0 1.1 1.2 0.4 0.5 0.6 0.7 0.8 0.9 0.1 0.4 0.7 0.2 0.5 0.8 0.3 0.6 0.9 1.0 1.1 1.2 dot product b=0.06 b=0.08 b=0.10 b=0.12 z = 0.20 z = 0.40 z = 0.60 z = 0.80 𝐳 = 𝑖=1 𝑚 (𝑤𝑖∙ 𝑖𝑛𝑝𝑢𝑡) + 𝑏𝑖𝑎𝑠 𝐚 = 𝜎 𝑧 = 0.1 ∙ 0.1 + 0.2 ∙ 0.2 + 0.3 ∙ 0.3 0.4 ∙ 0.1 + 0.5 ∙ 0.2 + 0.6 ∙ 0.3 0.7 ∙ 0.1 + 0.8 ∙ 0.2 + 0.9 ∙ 0.3 1.0 ∙ 0.1 + 1.1 ∙ 0.2 + 1.2 ∙ 0.3 = 0.14 0.32 0.50 0.68 = 0.14 0.32 0.50 0.68 + 0.06 0.08 0.10 0.12 = 𝟎. 𝟐𝟎 𝟎. 𝟒𝟎 𝟎. 𝟔𝟎 𝟎. 𝟖𝟎 0.1 0.2 0.3 ∙ 0.1 0.2 0.3
- 31. 0.1 0.2 0.3 1.0 1.1 1.2 0.4 0.5 0.6 0.7 0.8 0.9 0.1 0.4 0.7 0.2 0.5 0.8 0.3 0.6 0.9 1.0 1.1 1.2 dot product b=0.06 b=0.08 b=0.10 b=0.12 z = 0.20 z = 0.40 z = 0.60 z = 0.80 𝐳 = 𝑖=1 𝑚 (𝑤𝑖∙ 𝑖𝑛𝑝𝑢𝑡) + 𝑏𝑖𝑎𝑠 𝐚 = 𝜎 𝑧 = 0.1 ∙ 0.1 + 0.2 ∙ 0.2 + 0.3 ∙ 0.3 0.4 ∙ 0.1 + 0.5 ∙ 0.2 + 0.6 ∙ 0.3 0.7 ∙ 0.1 + 0.8 ∙ 0.2 + 0.9 ∙ 0.3 1.0 ∙ 0.1 + 1.1 ∙ 0.2 + 1.2 ∙ 0.3 = 0.14 0.32 0.50 0.68 = 0.14 0.32 0.50 0.68 = σ 0.20 0.40 0.60 0.80 + 0.06 0.08 0.10 0.12 = 𝟎. 𝟐𝟎 𝟎. 𝟒𝟎 𝟎. 𝟔𝟎 𝟎. 𝟖𝟎 0.1 0.2 0.3 ∙ 0.1 0.2 0.3
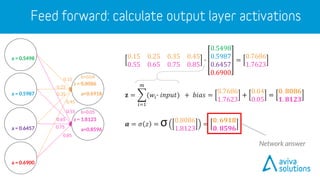
- 32. 0.1 0.2 0.3 1.0 1.1 1.2 0.4 0.5 0.6 0.7 0.8 0.9 0.1 0.4 0.7 0.2 0.5 0.8 0.3 0.6 0.9 1.0 1.1 1.2 dot product b=0.06 b=0.08 b=0.10 b=0.12 z = 0.20 a = 0.5498 z = 0.40 a = 0.5987 z = 0.60 a = 0.6457 z = 0.80 a = 0.6900 𝐳 = 𝑖=1 𝑚 (𝑤𝑖∙ 𝑖𝑛𝑝𝑢𝑡) + 𝑏𝑖𝑎𝑠 𝐚 = 𝜎 𝑧 = 0.1 ∙ 0.1 + 0.2 ∙ 0.2 + 0.3 ∙ 0.3 0.4 ∙ 0.1 + 0.5 ∙ 0.2 + 0.6 ∙ 0.3 0.7 ∙ 0.1 + 0.8 ∙ 0.2 + 0.9 ∙ 0.3 1.0 ∙ 0.1 + 1.1 ∙ 0.2 + 1.2 ∙ 0.3 = 0.14 0.32 0.50 0.68 = 0.14 0.32 0.50 0.68 = σ 0.20 0.40 0.60 0.80 + 0.06 0.08 0.10 0.12 = 𝟎. 𝟐𝟎 𝟎. 𝟒𝟎 𝟎. 𝟔𝟎 𝟎. 𝟖𝟎 0.1 0.2 0.3 = 𝟎. 𝟓𝟒𝟗𝟖 𝟎. 𝟓𝟗𝟖𝟕 𝟎. 𝟔𝟒𝟓𝟕 𝟎. 𝟔𝟗𝟎𝟎 ∙ 0.1 0.2 0.3
- 33. 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 ∙ 0.5498 0.5987 0.6457 0.6900 = 0.7686 1.7623 𝐳 = 𝑖=1 𝑚 (𝑤𝑖∙ 𝑖𝑛𝑝𝑢𝑡) + 𝑏𝑖𝑎𝑠 = 0.7686 1.7623 + 0.04 0.05 = 𝟎. 𝟖𝟎𝟖𝟔 𝟏. 𝟖𝟏𝟐𝟑 𝒂 = 𝜎 𝑧 = σ 0.8086 1.8123 = 𝟎. 𝟔𝟗𝟏𝟖 𝟎. 𝟖𝟓𝟗𝟔 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 b=0.04 b=0.05 z = 0.8086 a=0.6918 z = 1.8123 a=0.8596 a = 0.5498 a = 0.5987 a = 0.6457 a = 0.6900 Network answer
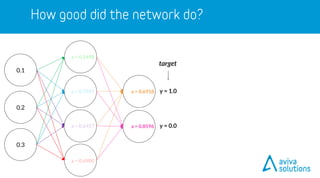
- 35. a = 0.5498 a = 0.5987 a = 0.6457 a = 0.6900 a = 0.6918 a = 0.8596 0.2 0.3 0.1
- 36. target y = 1.0 y = 0.0 a = 0.5498 a = 0.5987 a = 0.6457 a = 0.6900 a = 0.6918 a = 0.8596 0.2 0.3 0.1
- 37. target y = 1.0 y = 0.0 Quadratic Cost Function: (output - target) 2 a = 0.5498 a = 0.5987 a = 0.6457 a = 0.6900 a = 0.6918 a = 0.8596 0.2 0.3 0.1
- 38. target y = 1.0 y = 0.0 Quadratic Cost Function: (output - target) 2 Cost (0.6918 - 1.0)2 = 0.09498 (0.8596 - 0.0)2 = 0.7390 a = 0.5498 a = 0.5987 a = 0.6457 a = 0.6900 a = 0.6918 a = 0.8596 0.2 0.3 0.1
- 39. target y = 1.0 y = 0.0 Quadratic Cost Function: (output - target) 2 Total cost for this example = 0.83395 + Cost (0.6918 - 1.0)2 = 0.09498 (0.8596 - 0.0)2 = 0.7390 a = 0.5498 a = 0.5987 a = 0.6457 a = 0.6900 a = 0.6918 a = 0.8596 0.2 0.3 0.1
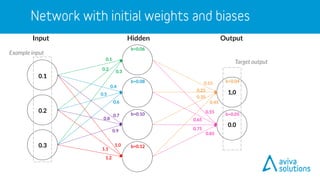
- 43. 3x4 + 4x2 = 20 weights 4 + 2 = 6 biases ↓ 0.1 0.2 0.3 1.0 1.1 1.2 0.4 0.5 0.6 0.7 0.8 0.9 b=0.06 b=0.08 b=0.10 b=0.12 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 b=0.04 b=0.05 Input OutputHidden 26 parameters
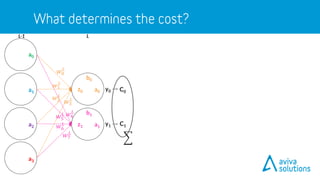
- 48. 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0a0z0 a0 LL-1 y0 b0 𝑤0 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 y0 y1a1z1 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿
- 49. 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0a0z0 a0 LL-1 y0 b0 𝑤0 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 y0 y1a1z1 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿
- 50. 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝑎 𝐿−2 𝑧 𝐿−1 𝑏 𝐿−1 𝑤 𝐿−1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0a0z0 a0 LL-1 y0 b0 𝑤0 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 y0 y1a1z1 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿
- 51. 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝑎 𝐿−2 𝑧 𝐿−1 𝑏 𝐿−1 𝑤 𝐿−1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0a0z0 a0 LL-1 y0 b0 𝑤0 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 y0 y1a1z1 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿
- 52. 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0a0z0 a0 LL-1 y0 b0 𝑤0 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 y0 y1a1z1 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿
- 53. LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 54. LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
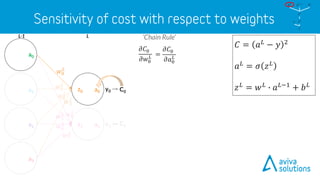
- 55. 𝜕𝐶0 𝜕𝑤0 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 = ‘Chain Rule’ y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 56. 𝜕𝐶0 𝜕𝑎0 𝐿 𝜕𝐶0 𝜕𝑤0 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 = ‘Chain Rule’ y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 57. 𝜕𝐶0 𝜕𝑎0 𝐿 𝜕𝐶0 𝜕𝑤0 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 = ∙ ‘Chain Rule’ y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 58. 𝜕𝐶0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝜕𝑤0 𝐿 𝜕𝐶0 𝜕𝑤0 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 = ∙ ∙ ‘Chain Rule’ y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 59. 𝜕𝐶0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝜕𝑤0 𝐿 𝜕𝐶0 𝜕𝑤0 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 = ∙ ∙ 𝜕𝐶0 𝜕𝑎0 𝐿 = 2 𝑎0 𝐿 − 𝑦y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 60. 𝜕𝐶0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝜕𝑤0 𝐿 𝜕𝐶0 𝜕𝑤0 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 = ∙ ∙ 𝜕𝐶0 𝜕𝑎0 𝐿 = 2 𝑎0 𝐿 − 𝑦 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 = 𝜎′ 𝑧0 𝐿 y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 61. 𝜕𝐶0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝜕𝑤0 𝐿 𝜕𝐶0 𝜕𝑤0 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 = ∙ ∙ 𝜕𝐶0 𝜕𝑎0 𝐿 = 2 𝑎0 𝐿 − 𝑦 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 = 𝜎′ 𝑧0 𝐿 y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝜎′ 𝑧 = 𝜎 𝑧 ∙ (1 − 𝜎 𝑧 )
- 62. 𝜕𝐶0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝜕𝑤0 𝐿 𝜕𝐶0 𝜕𝑤0 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 = ∙ ∙ 𝜕𝐶0 𝜕𝑎0 𝐿 = 2 𝑎0 𝐿 − 𝑦 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 = 𝜎′ 𝑧0 𝐿 𝜕𝑧0 𝐿 𝜕𝑤0 𝐿 = 𝑎0 𝐿−1 y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 63. 𝜕𝐶0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝜕𝑤0 𝐿 𝜕𝐶0 𝜕𝑤0 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝜕𝑎0 𝐿 𝜕𝑧0 𝐿 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 = ∙ ∙ 𝜕𝐶0 𝜕𝑤0 𝐿 = 2 𝑎0 𝐿 − 𝑦0 ∙ 𝜎′ 𝑧0 𝐿 ∙ 𝑎0 𝐿−1 y0 y1a1z1 a0 a1 a2 a3 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
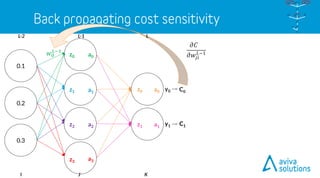
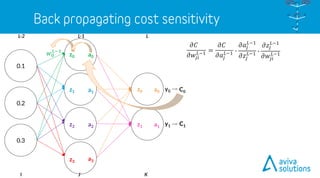
- 64. LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝐿 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 𝑤2 𝐿 𝑤1 𝐿 𝑤0 𝐿 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑎𝑗 𝐿−1 𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑤 𝑘𝑗 𝐿 𝑤3 𝐿 𝑤6 𝐿 𝑤5 𝐿 𝑤4 𝐿 𝑤7 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 65. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0=1.0 y1=0.0 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑎𝑗 𝐿−1𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑤 𝑘𝑗 𝐿 → a1=0.8596 Z1=1.8123 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85
- 66. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0=1.0 y1=0.0 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑎𝑗 𝐿−1𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑤 𝑘𝑗 𝐿 → a1=0.8596 Z1=1.8123 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 𝑤00 𝐿 → 2(0.6918 − 1.0) ∙ 𝜎′(0.8086) ∙ 0.5498 𝑤01 𝐿 → 2(0.6918 − 1.0) ∙ 𝜎′(0.8086) ∙ 0.5987 𝑤02 𝐿 → 2(0.6918 − 1.0) ∙ 𝜎′(0.8086) ∙ 0.6457 𝑤03 𝐿 → 2(0.6918 − 1.0) ∙ 𝜎′(0.8086) ∙ 0.6900 𝑤10 𝐿 → 2(0.8596 − 0.0) ∙ 𝜎′(1.8123) ∙ 0.5498 𝑤11 𝐿 → 2(0.8596 − 0.0) ∙ 𝜎′(1.8123) ∙ 0.5987 𝑤12 𝐿 → 2(0.8596 − 0.0) ∙ 𝜎′(1.8123) ∙ 0.6457 𝑤13 𝐿 → 2(0.8596 − 0.0) ∙ 𝜎′(1.8123) ∙ 0.6900
- 67. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0=1.0 y1=0.0 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑎𝑗 𝐿−1𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑤 𝑘𝑗 𝐿 → = 2 ∙ 0.6918 − 1 0.8596 − 0 × 𝜎′(0.8086) 𝜎′(1.8123) ⊗ 0.5498 0.5987 0.6457 0.6900 a1=0.8596 Z1=1.8123 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85
- 68. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0=1.0 y1=0.0 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑎𝑗 𝐿−1𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑤 𝑘𝑗 𝐿 → = −0.616 1.719 × 0.213 0.121 ⊗ 0.5498 0.5987 0.6457 0.6900 = 2 ∙ 0.6918 − 1 0.8596 − 0 × 𝜎′(0.8086) 𝜎′(1.8123) ⊗ 0.5498 0.5987 0.6457 0.6900 a1=0.8596 Z1=1.8123 Pointwise Multiply 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85
- 69. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0=1.0 y1=0.0 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑎𝑗 𝐿−1𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑤 𝑘𝑗 𝐿 → = −0.616 1.719 × 0.213 0.121 ⊗ 0.5498 0.5987 0.6457 0.6900 = −0.131 0.207 ⊗ 0.5498 0.5987 0.6457 0.6900 = 2 ∙ 0.6918 − 1 0.8596 − 0 × 𝜎′(0.8086) 𝜎′(1.8123) ⊗ 0.5498 0.5987 0.6457 0.6900 a1=0.8596 Z1=1.8123 Outer Product 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85
- 70. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0=1.0 y1=0.0 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑎𝑗 𝐿−1𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑤 𝑘𝑗 𝐿 → = −0.616 1.719 × 0.213 0.121 ⊗ 0.5498 0.5987 0.6457 0.6900 = −0.131 ∙ 0.5498 −0.131 ∙ 0.5987 −0.131 ∙ 0.6457 −0.131 ∙ 0.6900 0.207 ∙ 0.5498 0.207 ∙ 0.5987 0.207 ∙ 0.6457 0.207 ∙ 0.6900 = −0.131 0.207 ⊗ 0.5498 0.5987 0.6457 0.6900 = 2 ∙ 0.6918 − 1 0.8596 − 0 × 𝜎′(0.8086) 𝜎′(1.8123) ⊗ 0.5498 0.5987 0.6457 0.6900 a1=0.8596 Z1=1.8123 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85
- 71. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0=1.0 y1=0.0 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑎𝑗 𝐿−1𝜕𝐶 𝜕𝑤 𝑘𝑗 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑤 𝑘𝑗 𝐿 → = −0.616 1.719 × 0.213 0.121 ⊗ 0.5498 0.5987 0.6457 0.6900 = −0.131 ∙ 0.5498 −0.131 ∙ 0.5987 −0.131 ∙ 0.6457 −0.131 ∙ 0.6900 0.207 ∙ 0.5498 0.207 ∙ 0.5987 0.207 ∙ 0.6457 0.207 ∙ 0.6900 = −0.131 0.207 ⊗ 0.5498 0.5987 0.6457 0.6900 = −0.0723 −0.0787 −0.0848 −0.0907 0.1141 0.1242 0.1339 0.1431 = 2 ∙ 0.6918 − 1 0.8596 − 0 × 𝜎′(0.8086) 𝜎′(1.8123) ⊗ 0.5498 0.5987 0.6457 0.6900 a1=0.8596 Z1=1.8123 Weight Gradients 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85
- 72. LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 b0 b1 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 73. 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 𝜕𝐶 𝜕𝑎 𝑘 𝐿 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 b0 b1 = 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 74. 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 𝜕𝐶 𝜕𝑎 𝑘 𝐿 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 b0 b1 𝛿 𝑘 𝐿 ∙= ‘node delta’ = 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 75. 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 ∙ b0 b1 𝛿 𝑘 𝐿 = 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝛿 𝑘 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿
- 76. 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 ∙ b0 b1 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 = 1 𝛿 𝑘 𝐿 = 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝛿 𝑘 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿
- 77. 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 ∙ b0 b1 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 = 1 𝛿 𝑘 𝐿 = 𝜕𝐶 𝜕𝑏 𝑘 𝐿 = 𝛿 𝑘 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝛿 𝑘 𝐿 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿
- 78. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0 y1 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 = 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 → a1=0.8596 Z1=1.8123 𝜕𝐶 𝜕𝑏 𝑘 𝐿 = 𝛿 𝑘 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 b0 =0.04 b1 =0.05 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 79. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0 y1 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 = 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 → a1=0.8596 Z1=1.8123 = 2 ∙ 0.6918 − 1 0.8596 − 0 × 𝜎′(0.8086) 𝜎′(1.8123) 𝜕𝐶 𝜕𝑏 𝑘 𝐿 = 𝛿 𝑘 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 b0 =0.04 b1 =0.05 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 80. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0 y1 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 = 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 → = −0.616 1.719 × 0.213 0.121 a1=0.8596 Z1=1.8123 = 2 ∙ 0.6918 − 1 0.8596 − 0 × 𝜎′(0.8086) 𝜎′(1.8123) 𝜕𝐶 𝜕𝑏 𝑘 𝐿 = 𝛿 𝑘 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 b0 =0.04 b1 =0.05 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 81. LL-1 C0 C1 a0=0.6918 Z0=0.8086 y0 y1 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 KJ 𝜕𝐶 𝜕𝑏 𝑘 𝐿 = 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑏 𝑘 𝐿 → = −0.616 1.719 × 0.213 0.121 = −0.1314 0.2075 a1=0.8596 Z1=1.8123 Bias Gradients = 2 ∙ 0.6918 − 1 0.8596 − 0 × 𝜎′(0.8086) 𝜎′(1.8123) 𝜕𝐶 𝜕𝑏 𝑘 𝐿 = 𝛿 𝑘 𝐿 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 b0 =0.04 b1 =0.05 = 𝜹 𝒌 𝑳 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 82. Calculating output layer gradients
- 83. LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑤0 𝐿 𝑤4 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 84. ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝜕𝐶 𝜕𝑎 𝑘 𝐿 ∙ 𝜕𝑎 𝑘 𝐿 𝜕𝑧 𝑘 𝐿 𝑤0 𝐿 𝑤4 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 85. ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑤0 𝐿 𝑤4 𝐿 𝛿 𝑘 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 86. ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 = 𝑤 𝑘𝑗 𝐿 𝑤0 𝐿 𝑤4 𝐿 𝛿 𝑘 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 87. ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 = 𝑤 𝑘𝑗 𝐿 𝑤0 𝐿 𝑤4 𝐿 𝛿 𝑘 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 88. ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 = 𝑤 𝑘𝑗 𝐿 𝑤0 𝐿 𝑤4 𝐿 𝛿 𝑘 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 89. ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 = 𝑤 𝑘𝑗 𝐿 𝑤0 𝐿 𝑤4 𝐿 𝛿 𝑘 𝐿 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
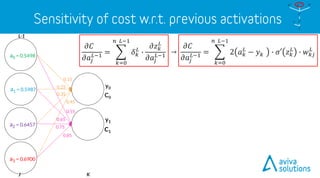
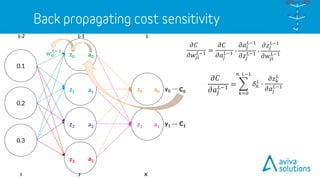
- 90. LL-1 𝐶 = 𝑎 𝐿 − 𝑦 2 𝑎 𝐿 = 𝜎 𝑧 𝑧 𝐿 = 𝑤 𝐿 ∙ 𝑎 𝐿−1 + 𝑏 𝐿 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 KJ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 = 𝑤 𝑘𝑗 𝐿 𝑤0 𝐿 𝑤4 𝐿 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦
- 91. L-1 C0 C1 y0 y1 KJ → 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900
- 92. L-1 C0 C1 𝜹 𝟎 = -0,131 y0 y1 KJ → 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 = −0.131 0.207 𝜹 𝒌 𝑳 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 𝜹 𝟏 = 0,207 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900
- 93. L-1 C0 C1 𝜹 𝟎 = -0,131 y0 y1 KJ → 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 = −0.131 0.207 𝜹 𝒌 𝑳 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 𝜹 𝟏 = 0,207 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 𝑎1 𝐿−1 → (−0.131 ∙ 0.25 + 0.207 ∙ 0.65) 𝑎2 𝐿−1 → (−0.131 ∙ 0.35 + 0.207 ∙ 0.75) 𝑎3 𝐿−1 → (−0.131 ∙ 0.45 + 0.207 ∙ 0.85) 𝑎0 𝐿−1 → (−0.131 ∙ 0.15 + 0.207 ∙ 0.55)
- 94. L-1 C0 C1 𝜹 𝟎 = -0,131 y0 y1 KJ → 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 = −0.131 0.207 −0.131 0.207 𝜹 𝒌 𝑳 ∙ 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = dot product 𝜹 𝟏 = 0,207 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900
- 95. L-1 C0 C1 𝜹 𝟎 = -0,131 y0 y1 KJ → 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 = −0.131 0.207 −0.131 0.207 𝜹 𝒌 𝑳 ∙ 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝜹 𝟏 = 0,207 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900 (−0.131 ∙ 0.15 + 0.207 ∙ 0.55) (−0.131 ∙ 0.25 + 0.207 ∙ 0.65) (−0.131 ∙ 0.35 + 0.207 ∙ 0.75) (−0.131 ∙ 0.45 + 0.207 ∙ 0.85)
- 96. L-1 C0 C1 𝜹 𝟎 = -0,131 y0 y1 KJ → = 0.0944 0.1020 0.1096 0.1172Previous Activation Gradients 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 ∙ 𝑤 𝑘𝑗 𝐿 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 = 2 𝑎 𝑘 𝐿 − 𝑦 𝑘 ∙ 𝜎′ 𝑧 𝑘 𝐿 = −0.131 0.207 −0.131 0.207 𝜹 𝒌 𝑳 = (−0.131 ∙ 0.15 + 0.207 ∙ 0.55) (−0.131 ∙ 0.25 + 0.207 ∙ 0.65) (−0.131 ∙ 0.35 + 0.207 ∙ 0.75) (−0.131 ∙ 0.45 + 0.207 ∙ 0.85) ∙ 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = 𝜹 𝟏 = 0,207 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 a0 = 0.5498 a1 = 0.5987 a2 = 0.6457 a3 = 0.6900
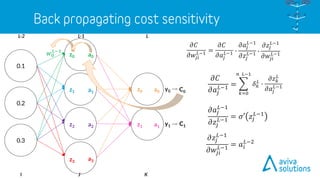
- 97. L-1 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 𝑤0 𝐿−1 0.2 0.3 0.1 L-2 z0 z1 z2 z3 𝜕𝐶 𝜕𝑤𝑗𝑖 𝐿−1 KJI 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝑎 𝐿−2 𝑧 𝐿 𝑏 𝐿−1 𝑤 𝐿−1 L
- 98. L-1 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 𝑤0 𝐿−1 0.2 0.3 0.1 L-2 z0 z1 z2 z3 𝜕𝐶 𝜕𝑤𝑗𝑖 𝐿−1 = 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 ∙ 𝜕𝑎𝑗 𝐿−1 𝜕𝑧𝑗 𝐿−1 ∙ 𝜕𝑧𝑗 𝐿−1 𝜕𝑤𝑗𝑖 𝐿−1 KJI 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝑎 𝐿−2 𝑧 𝐿 𝑏 𝐿−1 𝑤 𝐿−1 L
- 99. L-1 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 𝑤0 𝐿−1 0.2 0.3 0.1 L-2 z0 z1 z2 z3 𝜕𝐶 𝜕𝑤𝑗𝑖 𝐿−1 = 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 ∙ 𝜕𝑎𝑗 𝐿−1 𝜕𝑧𝑗 𝐿−1 ∙ 𝜕𝑧𝑗 𝐿−1 𝜕𝑤𝑗𝑖 𝐿−1 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = KJI 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝑎 𝐿−2 𝑧 𝐿 𝑏 𝐿−1 𝑤 𝐿−1 L 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1
- 100. L-1 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 𝑤0 𝐿−1 0.2 0.3 0.1 L-2 z0 z1 z2 z3 𝜕𝐶 𝜕𝑤𝑗𝑖 𝐿−1 = 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 ∙ 𝜕𝑎𝑗 𝐿−1 𝜕𝑧𝑗 𝐿−1 ∙ 𝜕𝑧𝑗 𝐿−1 𝜕𝑤𝑗𝑖 𝐿−1 𝜕𝑎𝑗 𝐿−1 𝜕𝑧𝑗 𝐿−1 = 𝜎′ 𝑧𝑗 𝐿−1 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = KJI 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝑎 𝐿−2 𝑧 𝐿 𝑏 𝐿−1 𝑤 𝐿−1 L 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1
- 101. L-1 C0 C1 a0z0 y0 y1a1z1 a0 a1 a2 a3 𝑤0 𝐿−1 0.2 0.3 0.1 L-2 z0 z1 z2 z3 𝜕𝐶 𝜕𝑤𝑗𝑖 𝐿−1 = 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 ∙ 𝜕𝑎𝑗 𝐿−1 𝜕𝑧𝑗 𝐿−1 ∙ 𝜕𝑧𝑗 𝐿−1 𝜕𝑤𝑗𝑖 𝐿−1 𝜕𝑎𝑗 𝐿−1 𝜕𝑧𝑗 𝐿−1 = 𝜎′ 𝑧𝑗 𝐿−1 𝜕𝑧𝑗 𝐿−1 𝜕𝑤𝑗𝑖 𝐿−1 = 𝑎𝑖 𝐿−2 𝜕𝐶 𝜕𝑎𝑗 𝐿−1 = KJI 𝑎 𝐿−1 𝑧 𝐿 𝑏 𝐿 𝑤 𝐿 𝑎 𝐿 𝐶 𝑦 𝑎 𝐿−2 𝑧 𝐿 𝑏 𝐿−1 𝑤 𝐿−1 L 𝑘=0 𝑛 𝐿−1 𝛿 𝑘 𝐿 ∙ 𝜕𝑧 𝑘 𝐿 𝜕𝑎𝑗 𝐿−1
- 102. Calculating previous activation gradients
- 104. 𝐃𝐞𝐥𝐭𝐚𝐖𝐞𝐢𝐠𝐡𝐭 = LearningRate ∙ WeightGradient 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 b=0.04 b=0.05 −0.0723 −0.0787 −0.0848 −0.0907 0.1141 0.1242 0.1339 0.1431 = −0.0361 −0.0393 −0.0424 −0.0453 0.057 0.062 0.0670 0.0716 a0 a1 a2 a3 = 0.5 ×
- 105. 𝐃𝐞𝐥𝐭𝐚𝐖𝐞𝐢𝐠𝐡𝐭 = LearningRate ∙ WeightGradient 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 b=0.04 b=0.05 𝐍𝐞𝐰𝐖𝐞𝐢𝐠𝐡𝐭 = Weight − DeltaWeight −0.0723 −0.0787 −0.0848 −0.0907 0.1141 0.1242 0.1339 0.1431 = −0.0361 −0.0393 −0.0424 −0.0453 0.057 0.062 0.0670 0.0716 = 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 = 0.1861 0.2893 0.3924 0.4953 0.4930 0.5879 0.6830 0.7784 − −0.0361 −0.0393 −0.0424 −0.0453 0.057 0.062 0.0670 0.0716 a0 a1 a2 a3 = 0.5 ×
- 106. 𝐃𝐞𝐥𝐭𝐚𝐁𝐢𝐚𝐬 = LearningRate ∙ BiasGradient 0.15 0.25 0.35 0.45 0.55 0.65 0.75 0.85 b=0.04 b=0.05 𝐍𝐞𝐰𝐁𝐢𝐚𝐬 = Bias − DeltaBias −0.1314 0.2075 = −0.0657 0.1037 = 0.04 0.05 = 0.1057 −0.0537 − −0.0657 0.1037 a0 a1 a2 a3 = 0.5 ×
- 107. Updating weights and biases
- 110. http://yann.lecun.com/exdb/mnist/ Modified National Institute of Standards and Technology database