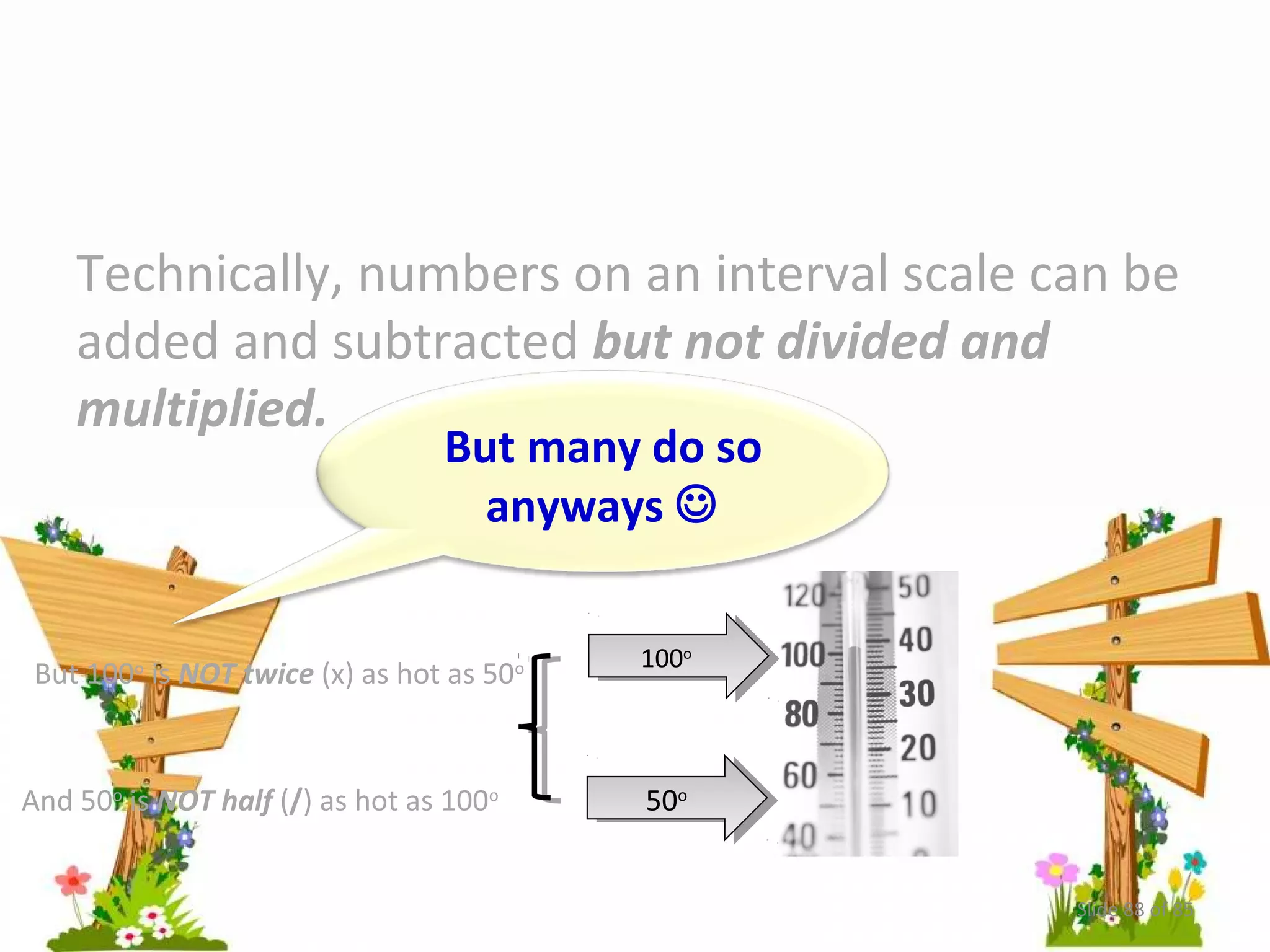
The document discusses different types of measurement scales used in quantitative research. Nominal scales use numbers as labels for categories with no implied order or quantity. Ordinal scales represent relative amounts of an attribute, where higher numbers indicate more of the attribute, but intervals between points are undefined. Interval and ratio scales also represent quantities, with interval scales having equal intervals and ratio scales having a meaningful zero point.