PCA_2022-In_and_out.pptx zxczxczxczxczxcxzczx
- 1. Principal Component Analysis (PCA) – In vs. Out of Model 1 Rodolfo J. Romañach, Ph.D. QUIM 6835 Chemometrcs February 23, 2022
- 2. “a database is not a vault, it is a garden.“ Rene Marie Pacella 2
- 3. Scores Provide a MAP of Samples Loadings Provide a MAP of Variable Interrelationships Esbensen KH (2012) Multivariate Data Analysis- in practice. 5th edn. CAMO Software, page 44. Scores cannot be interpreted without loadings; loadings cannot be interpreted without scores.
- 4. “Loadings describe the data structure in terms of variable contributions and correlations. Every variable analyzed has a loading on each PC, which reflects how much the individual variable contributes to that PC, and how well the PC takes into account the variation contained in a variable.” Loadings Score Plots Loadings Line Plots
- 5. “Loadings describe the data structure in terms of variable contributions and correlations. Every variable analyzed has a loading on each PC, which reflects how much the individual variable contributes to that PC, and how well the PC takes into account the variation contained in a variable.”
- 6. Loadings • Loadings – map of variables. • “The PCs are in fact nothing but linear combinations of the original variables (unit vectors). Returning to a previous definition, the loadings provide a “weighting” of each variable’s contribution to a PC direction. When a weighting is high for a variable, i.e. the variable has a high loading (numerically), this variable contributes significantly to the variance expressed by that PC.” • X = TPT + E • TPT describes the model. E is not the model, it is the residual variation that is not included in the model. Esbensen, K. E.; Swarbrick, B., Multivariate Data Analysis – in practice. An Introduction. 6th ed.; IMPublishing: 2018. page 78.
- 7. If the spectral noise is known to be 0.1%, then how many principal components should be used to explain the data ? Here we have the opportunity to filter or reduce the spectral noise since we do not have to keep the eight factors. Principal Components Analysis (PCA)
- 8. Principal Component Analysis • X = TPT + E • TPT describes the model. E is not the model, it is the residual variation that is not included in the model. • This is a description of PCA, but more importantly it follows: Data structure is correlated with the property of interest, while noise is everything else, such as instrumental noise (high frequency, low frequency noise, etc). Noise is what is not included within the model (data structure) – unexplained Esbensen KH (2012) Multivariate Data Analysis- in practice. 5th edn. CAMO Software,
- 9. 95% Confidence Interval The distance from the multivariate mean, commonly referred to as the Mahalanobis distance (MD), is computed with the scores. In Hotelling’s T2 test, the squared MD values are called Hotelling’s T2 values which are compared with a table of critical values. De Maesschalck, R.; Jouan-Rimbaud, D.; Massart, D. L., The Mahalanobis distance. Chemometrics Intellig. Lab. Syst. 2000, 50 (1), 1-18.
- 10. Understanding Hotelling’s T2 Test • In univariate statistics the t-test is used to estimate confidence interval for one variable. • This is the estimation of confidence interval for a multivariate system. • Confidence limits are built using the training set which would contain measurements that represent the normal (in control) situation. • The computed MD (the so-called T2 value) of each value is compared to a critical T2 value. • Used to build multivariate process control charts using the original variables or PCs.
- 11. Euclidean & Mahalonobis Distance The Euclidean distance would tell us the distance traveled. However, if there is bad weather or there are many airplanes trying to land the distance traveled would be greater. The distance traveled would not be the same for every flight. In that case we could calculate a Mahalanobis distance based on the standard deviations of the actual travel distances. The Mahalanobis distance is thus a statistical distance.
- 12. Projection of Samples Into Model • Once the PCA model is developed you can project samples into this model. • “Projection is the method of taking a new object and “transforming” it through the loadings of an existing model to produce a new score value in multivariate space.”-Esbensen page 151. • “a new object can be projected onto an existing model and the position of the new object can be determined as being part of the model population, or as being distinctly different. Esbensen page 151” Esbensen, K. E.; Swarbrick, B., Multivariate Data Analysis – in practice. An Introduction. 6th ed.; IMPublishing: 2018.
- 13. PCA Score Plot The calibration set (Red points, 0-14.46 %w/w) was used to predict blends of 20% w/w with a different API (Blue) and excipients under the same spectral acquisition parameters. These are outside the 95% CI of model.
- 14. What are Outliers? • Outliers are unusual samples that have a different pattern that the rest of the samples, and could require an extra factor to describe them. – Pirouette • “Any observation that does not fit a pattern” - Miller • Outliers may be measurement errors, for example when there is no sample in front of Raman or NIR probe, and it just sees air. • “Some packages include elaborate diagnostics for so- called outliers, which may in many cases be perfectly good samples but ones whose correlation structure differs from that of the training set.” - Brereton Pirouette Manual, page 5-23 . Chemometrics. Data Analysis for the Laboratory and Chemical Plant. Richard G. Brereton, Wiley, 2003, Page 72. Miller, Chemometrics in Process Analytical Chemistry. 14
- 15. PCA and outliers • PCA is a good tool for visualization of outliers in the X data. Visualizing spectra or samples that do not follow the same pattern as the rest. • If a sample’s score is separated from others it may be an outlier. We may not know the reason for the outlier, but if we pin-point it that’s a start. Later on we can determine a physical or chemical reason for the outlier. • The score and error contributes indicate which variables may cause the sample to be different. • PCA model can be used as a benchmark for future samples. Pirouette Manual. 5-14, and 5-19. Infometrix. 15
- 16. In Model vs. Out of Model
- 17. In-Model vs. Out of Model • Hotelling’s T2 test indicates whether a sample is an outlier based on scores (variation captured by model). • The X-residuals provides an “out of model” – assessment of outliers. The Q statistic flags samples with unusual outliers. • These are two complementary views, and often used in real time process measurements. 17 Pirouette Manual 4.02, Infometrix, page 5-25 *- The Q statistic is also referred to as the square prediction error (squared residual variance) . The value of Q can be obtained from its approximate distribution. Pirouette manual 5-24.
- 18. Real Time Latent Variable Predictor YES Spectrum similar to calib.model predict blend conc. Other calib model Outlier (inst. malfunction or process change) Analytical methods are not applicable to all materials, they are applicable to a certain formulation or product. First test with PCA determines applicability of method.
- 19. Process Control Application – using the Calib. Model
- 20. Control hardware and software integration Computers and Chemical Engineering 66 (2014) 186–200 Step 2 – Method for RT analysis Step 3 – sensors integrated into plant Step 4 – signal to Control platform Step 1 - Design
- 21. Industrial Application • Software like SIMCA, Unscrambler, Pirouette, PLS Tool Box, PLS IQ, etc are used to develop the calibration model. • This is another software that is just for “use” of the calibration model and provide the information to a distributed control system or plant manufacturing data system. • A number of companies sell software for real time predictions. Software that enable the use of the regression equation in the production environment. • Significant opportunity for quality improvement and process knowledge.
- 22. Principal Component Analysis (PCA) – In vs. Out of Model – Importance of Residuals 22 Rodolfo J. Romañach, Ph.D. QUIM 6835 Chemometrcs March 4, 2022
- 23. Projection of Samples Into Model • Use an existing model to predict unknown samples. • Once the PCA model is developed you can project samples into this model. • “Projection is the method of taking a new object and “transforming” it through the loadings of an existing model to produce a new score value in multivariate space.”-Esbensen page 151. • “a new object can be projected onto an existing model and the position of the new object can be determined as being part of the model population, or as being distinctly different.” Esbensen page 151, section 6.7. Esbensen, K. E.; Swarbrick, B., Multivariate Data Analysis – in practice. An Introduction. 6th ed.; IMPublishing: 2018.
- 24. Projection to 2-Factor PCA Model (in within Mahalanobis, but out in terms of residuals) 0 4 8 12 16 Mahalanobis Distance 0.01 0.02 0.03 0.04 0.05 Sample Residual 3
- 25. X-Residuals after 2Factors and Projection to PCA model Plot of variation that is not included in the model.
- 26. X-Residuals after 3 Factors and Projection to PCA model Plot of variation that is not included in the model.
- 27. Projection of Samples Into Model • You used an existing model (0 -14.46% w/w samples) to predict unknown samples. • Once the PCA model is developed you can project samples into this model. • “Projection is the method of taking a new object and “transforming” it through the loadings of an existing model to produce a new score value in multivariate space.”-Esbensen page 151. • “a new object can be projected onto an existing model and the position of the new object can be determined as being part of the model population, or as being distinctly different.” Esbensen page 151, section 6.7. Esbensen, K. E.; Swarbrick, B., Multivariate Data Analysis – in practice. An Introduction. 6th ed.; IMPublishing: 2018.
- 28. Prediction of 2 samples Two spectra were predicted as unknowns: 1. the 7.29% (w/w) spectrum that is already in the calibration model. 2. Noise spectrum + 7.29% (w/w) spectrum that is already in the calibration model. They were predicted by 0 – 14.46% (w/w) calibration model developed in the laboratory session. The Prediction command was used to predict with a stored model.
- 29. Projection of Unknown Samples into PCA Model Scores 3D
- 31. Predict Scores 2D Zoomed
- 32. In and Out PCA Model – 1 Factor
- 33. In and Out PCA Model – 2 Factors
- 34. In and Out PCA Model – 3 Factors
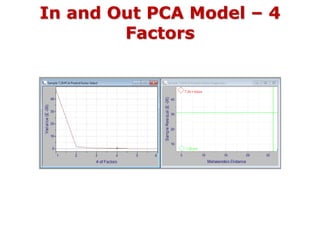
- 35. In and Out PCA Model – 4 Factors
- 36. Sample Residual in PCA • X = TPT + E • TPT describes the model. E is not the model, it is the residual variation that is not included in the model. In model – scores based. • A sample could have a large distance to the center of the model described by TPT, be far away from the center. Exceed the 95% confidence interval. Out model – residuals based. • A sample could also have a E larger than the 95% CI of the model. The sample residual exceeds the residual variation calculated with all the samples in the model. This is what happened to the 7.29% (w/w) sample + noise. Esbensen KH (2012) Multivariate Data Analysis- in practice. 5th edn. CAMO Software, and equation 5-23 in Pirouette manual.
- 37. Sample Residual in PCA If a particular sample residual exceeds the residual of the model, it could be considered an outlier, “it might not belong to the same population as the other samples in the training set.” Pirouette manual, Sample Residual topic (5.23 – 5.28) An F-test is used (si is for the sample, s0 for the variance of model. A threshold is then calculated as shown in the plot
- 38. Q-Statistic • This is referred to the squared prediction error. Q is related to the sample residual variance but without normalization. • Also used to evaluate whether a sample might be an outlier. The critical value of Q can be calculated from its approximate distribution. Pirouette manual, Chapter 5, Q-Statistic, equation 5.29
- 39. Probability • Consider a probability cutoff of 95%. The null hypothesis is that the variances are equal. If the probability value corresponding to the F value exceeds 95% then the hypothesis is rejected, and it is inferred that the sample was not drawn from the same population. • As the samples probability approaches 1, then the chance that it is an outlier increases. Pirouette chapter 5, Probability (page 5-24)
- 40. Mahalanobis Distance in PCA Pirouette manual, Chapter 5, page 5-25 Calculated for each sample, as a measure of variability. This is the distance from the multivariate mean. If a sample’s distance excees MDcrit, it may be an outlier.
- 41. Understanding Hotelling’s T2 Test • In univariate statistics the t-test is used to estimate confidence interval for one variable. • This is the estimation of confidence interval for a multivariate system. • Confidence limits are built using the training set which would contain measurements that represent the normal (in control) situation. • The computed MD (the so-called T2 value) of each value is compared to a critical T2 value. • Used to build multivariate process control charts using the original variables or PCs.
- 42. Principal Component Analysis (PCA)- Preamble to Quantitative Methods 42 Rodolfo J. Romañach, Ph.D. QUIM 6835 Chemometrcs February =------- 2022
- 43. A.U. Vanarase, M. Alcalà, J.I. Jerez Rozo, F.J. Muzzio and R.J. Romañach, “Real-time monitoring of drug concentration in a continuous powder mixing process using NIR spectroscopy, Chemical Engineering Science, 2010, 65(21), 5728 – 5733. PCA Scores Plot-The Transition from Qualitative to Quantitative The first PC shows that concentration is the main source of variation in the data. This qualitative observation is a good positive indication that a good quantitative model can be developed.
- 44. Introduction to Principal Component Analysis (PCA)- Discussion of Exercise 44 Rodolfo J. Romañach, Ph.D. QUIM 6835 Chemometrcs February =------- 2022
- 45. Spectra and PCA Score Plot
- 46. Spectra, PCA Score Plot, & Loadings Line Plot Comp No. M1.R2X M1.R2X(cum) Comp[1] 0.986703 0.986703 Comp[2] 0.0124451 0.999148 Orthogonality
- 47. What is the objective? • If the goal is to determine differences in baseline, then method development is completed. • If the goal is to differentiate between samples of different concentrations then more work is needed. Pretreatment of the data becomes necessary.
- 48. Spectra, PCA Score Plot, & Loadings Line Plot Comp No. M2.R2X M2.R2X Comp[1] 0.827293 0.827293 Comp[2] 0.146939 0.146939 Orthogonality
- 49. PCA – Orthogonality Obtained for spectra of 0 -15% (w/w) without pretreatment. Notice that first factor summarizes most of the variation, and then it starts decreasing. Each factor summarizes new variation, not included in previous factors. Pretreatment was not used, only mean centering. PCA After only Mean-Centering Variance Percent Cumulative Press Cal Factor1 5.48197 98.67 98.67034 0.073874 Factor2 0.06914 1.2445 99.91486 0.00473 Factor3 0.00403 0.0726 99.98741 0.000699 Factor4 0.00032 0.0057 99.99308 0.000384 Factor5 0.00027 0.0049 99.99799 0.000111 Factor6 5.8E-05 0.001 99.99904 0.000053 Factor7 3.5E-05 0.0006 99.99967 0.000018 Factor8 8E-06 0.0002 99.99983 0.000009
- 50. If the spectral noise is known to be 0.1%, then how many principal components should be used to explain the data ? Here we have the opportunity to filter or reduce the spectral noise since we do not have to keep the eight factors. Principal Components Analysis (PCA)
- 51. 95% Confidence Interval The distance from the multivariate mean, commonly referred to as the Mahalanobis distance (MD), is computed with the scores. In Hotelling’s T2 test, the squared MD values are called Hotelling’s T2 values which are compared with a table of critical values. De Maesschalck, R.; Jouan-Rimbaud, D.; Massart, D. L., The Mahalanobis distance. Chemometrics Intellig. Lab. Syst. 2000, 50 (1), 1-18.
- 52. Euclidean & Mahalonobis Distance The Euclidean distance would tell us the distance traveled. However, if there is bad weather or there are many airplanes trying to land the distance traveled would be greater. The distance traveled would not be the same for every flight. In that case we could calculate a Mahalanobis distance based on the standard deviations of the actual travel distances. The Mahalanobis distance is thus a statistical distance.
- 53. Principal Component Analysis (PCA) Introduction to Outlier Diagnostics & Projections 53 Rodolfo J. Romañach, Ph.D. QUIM 6835 Chemometrcs September 3, 2019 Class no. 7
- 54. Foods Example 2018 1. Spectra have been uploaded and category variables were added. 2. View the spectra. 3. Look at all spectra. Look at all flour spectra. 4. Perform 2nd derivative with 7 points. 5. Perform second derivative spectra. Savitzky Golay 19 points. 6. Select just one spectrum to view spectral differences. 7. Select limited number of spectra. 8. Look at all Flour spectra. Obtain shortened spectral range eliminating some of high frequency region. 9. Perform PCA of flour with 2nd der 19 points, in shortened spectral region (194-1063 variables).
- 55. Foods Example 2018- 2 1. View scores plot, and Hotelling’s limits, loadings plot (line and score plot), influence plot, explained variance. 2. Examine sample no. 2 more closely. 3. Review In and Out for Flour model. 4. Residual vs. Hotelling. 5. Predict samples 6 -10 of flour, as if they were unknowns. These should be projected within 95% confidence interval. 6. Perform a PCA of the pan criollo samples. 7. Project Whole wheat into pan criollo.
- 56. Vector Multiplication 56 For the product of two matrices to be defined, the number of columns of the first matrix must equal the number of rows of the second matrix. Show scores and loadings in software.
- 57. Vector Multiplication inner product, dot product, or scalar product, and seeing the vector as a one column or one row matrix. The length of a vector is Inner product obtained with vectors that have the same dimensions: x = [200 300 100 360] y = [380 580 420 840] x∙y = 200∙380 + 300∙580 + 100∙420 + 360∙840 x∙y = 594400 57 Matrix multiplication requires that the number of columns of first matrix = number of rows of second. m x n n x p = m x p Chapter 9 Vectors and matrices. In Data Handling in Science and Technology, Massart, D. L.; Vandeginste, B. G. M.; Buydens, L. M. C.; De Jong, S.; Lewi, P. J.; Smeyers-Verbeke, J., Eds. Elsevier: 1998; Vol. 20, pp 231-261.
- 58. Vector Multiplication Second way of writing the product, explains why it is called the dot product Matrix multiplication requires that the number of columns of first matrix = number of rows of second. m x n n x p = m x p Matrix multiplication is done by summing the products of ith element of a row with the ith element of a column. 58 Chapter 9 Vectors and matrices. In Data Handling in Science and Technology, Massart, D. L.; Vandeginste, B. G. M.; Buydens, L. M. C.; De Jong, S.; Lewi, P. J.; Smeyers-Verbeke, J., Eds. Elsevier: 1998; Vol. 20, pp 231-261.












































![Spectra, PCA Score Plot, & Loadings Line
Plot
Comp No. M1.R2X M1.R2X(cum)
Comp[1] 0.986703 0.986703
Comp[2] 0.0124451 0.999148
Orthogonality](https://image.slidesharecdn.com/pca2022-inandout-240526014902-70564a6a/85/PCA_2022-In_and_out-pptx-zxczxczxczxczxcxzczx-46-320.jpg)

![Spectra, PCA Score Plot, & Loadings Line
Plot
Comp No. M2.R2X M2.R2X
Comp[1] 0.827293 0.827293
Comp[2] 0.146939 0.146939
Orthogonality](https://image.slidesharecdn.com/pca2022-inandout-240526014902-70564a6a/85/PCA_2022-In_and_out-pptx-zxczxczxczxczxcxzczx-48-320.jpg)








![Vector Multiplication
inner product, dot product, or scalar product, and
seeing the vector as a one column or one row
matrix.
The length of a vector is
Inner product obtained with vectors that have the
same dimensions:
x = [200 300 100 360]
y = [380 580 420 840]
x∙y = 200∙380 + 300∙580 + 100∙420 + 360∙840
x∙y = 594400
57
Matrix multiplication requires that the number of columns of first
matrix = number of rows of second. m x n n x p = m x p
Chapter 9 Vectors and matrices. In Data Handling in Science and Technology,
Massart, D. L.; Vandeginste, B. G. M.; Buydens, L. M. C.; De Jong, S.; Lewi, P. J.;
Smeyers-Verbeke, J., Eds. Elsevier: 1998; Vol. 20, pp 231-261.](https://image.slidesharecdn.com/pca2022-inandout-240526014902-70564a6a/85/PCA_2022-In_and_out-pptx-zxczxczxczxczxcxzczx-57-320.jpg)
