![2
Propositional logic
• Logical constants: true, false
• Propositional symbols: P, Q, S, ... (atomic sentences)
• Wrapping parentheses: ( … )
• Sentences are combined by connectives:
...and [conjunction]
...or [disjunction]
...implies [implication / conditional]
..is equivalent [biconditional]
...not [negation]
• Literal: atomic sentence or negated atomic sentence](https://image.slidesharecdn.com/propositionallogic-240710082720-431fefa0/85/Propositional-Logic-for-discrete-structures-2-320.jpg)
Propositional Logic for discrete structures
- 1. 1 Propositional Logic Chapter 7.4-7.5, 7.7 CMSC 471 Adapted from slides by Tim Finin and Marie desJardins. Some material adopted from notes by Andreas Geyer-Schulz and Chuck Dyer
- 2. 2 Propositional logic • Logical constants: true, false • Propositional symbols: P, Q, S, ... (atomic sentences) • Wrapping parentheses: ( … ) • Sentences are combined by connectives: ...and [conjunction] ...or [disjunction] ...implies [implication / conditional] ..is equivalent [biconditional] ...not [negation] • Literal: atomic sentence or negated atomic sentence
- 3. 3 Examples of PL sentences • P means “It is hot.” • Q means “It is humid.” • R means “It is raining.” • (P Q) R “If it is hot and humid, then it is raining” • Q P “If it is humid, then it is hot” • A better way: Hot = “It is hot” Humid = “It is humid” Raining = “It is raining”
- 4. 4 Propositional logic (PL) • A simple language useful for showing key ideas and definitions • User defines a set of propositional symbols, like P and Q. • User defines the semantics of each propositional symbol: – P means “It is hot” – Q means “It is humid” – R means “It is raining” • A sentence (well formed formula) is defined as follows: – A symbol is a sentence – If S is a sentence, then S is a sentence – If S is a sentence, then (S) is a sentence – If S and T are sentences, then (S T), (S T), (S T), and (S ↔ T) are sentences – A sentence results from a finite number of applications of the above rules
- 5. 5 A BNF grammar of sentences in propositional logic S := <Sentence> ; <Sentence> := <AtomicSentence> | <ComplexSentence> ; <AtomicSentence> := "TRUE" | "FALSE" | "P" | "Q" | "S" ; <ComplexSentence> := "(" <Sentence> ")" | <Sentence> <Connective> <Sentence> | "NOT" <Sentence> ; <Connective> := "NOT" | "AND" | "OR" | "IMPLIES" | "EQUIVALENT" ;
- 6. 6 Some terms • The meaning or semantics of a sentence determines its interpretation. • Given the truth values of all symbols in a sentence, it can be “evaluated” to determine its truth value (True or False). • A model for a KB is a “possible world” (assignment of truth values to propositional symbols) in which each sentence in the KB is True.
- 7. 7 More terms • A valid sentence or tautology is a sentence that is True under all interpretations, no matter what the world is actually like or how the semantics are defined. Example: “It’s raining or it’s not raining.” • An inconsistent sentence or contradiction is a sentence that is False under all interpretations. The world is never like what it describes, as in “It’s raining and it’s not raining.” • P entails Q, written P |= Q, means that whenever P is True, so is Q. In other words, all models of P are also models of Q.
- 9. 9 Truth tables II The five logical connectives: A complex sentence:
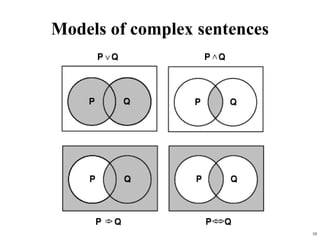
- 10. 10 Models of complex sentences
- 11. 11 Inference rules • Logical inference is used to create new sentences that logically follow from a given set of predicate calculus sentences (KB). • An inference rule is sound if every sentence X produced by an inference rule operating on a KB logically follows from the KB. (That is, the inference rule does not create any contradictions) • An inference rule is complete if it is able to produce every expression that logically follows from (is entailed by) the KB. (Note the analogy to complete search algorithms.)
- 12. 12 Sound rules of inference • Here are some examples of sound rules of inference – A rule is sound if its conclusion is true whenever the premise is true • Each can be shown to be sound using a truth table RULE PREMISE CONCLUSION Modus Ponens A, A B B And Introduction A, B A B And Elimination A B A Double Negation A A Unit Resolution A B, B A Resolution A B, B C A C
- 13. 13 Soundness of modus ponens A B A → B OK? True True True True False False False True True False False True
- 14. 14 Soundness of the resolution inference rule
- 15. 15 Proving things • A proof is a sequence of sentences, where each sentence is either a premise or a sentence derived from earlier sentences in the proof by one of the rules of inference. • The last sentence is the theorem (also called goal or query) that we want to prove. • Example for the “weather problem” given above. 1 Humid Premise “It is humid” 2 HumidHot Premise “If it is humid, it is hot” 3 Hot Modus Ponens(1,2) “It is hot” 4 (HotHumid)Rain Premise “If it’s hot & humid, it’s raining” 5 HotHumid And Introduction(1,2) “It is hot and humid” 6 Rain Modus Ponens(4,5) “It is raining”
- 16. 16 Horn sentences • A Horn sentence or Horn clause has the form: P1 P2 P3 ... Pn Q or alternatively P1 P2 P3 ... Pn Q where Ps and Q are non-negated atoms • To get a proof for Horn sentences, apply Modus Ponens repeatedly until nothing can be done • We will use the Horn clause form later (P Q) = (P Q)
- 17. 17 Entailment and derivation • Entailment: KB |= Q – Q is entailed by KB (a set of premises or assumptions) if and only if there is no logically possible world in which Q is false while all the premises in KB are true. – Or, stated positively, Q is entailed by KB if and only if the conclusion is true in every logically possible world in which all the premises in KB are true. • Derivation: KB |- Q – We can derive Q from KB if there is a proof consisting of a sequence of valid inference steps starting from the premises in KB and resulting in Q
- 18. 18 Two important properties for inference Soundness: If KB |- Q then KB |= Q – If Q is derived from a set of sentences KB using a given set of rules of inference, then Q is entailed by KB. – Hence, inference produces only real entailments, or any sentence that follows deductively from the premises is valid. Completeness: If KB |= Q then KB |- Q – If Q is entailed by a set of sentences KB, then Q can be derived from KB using the rules of inference. – Hence, inference produces all entailments, or all valid sentences can be proved from the premises.
- 19. 19 Propositional logic is a weak language • Hard to identify “individuals” (e.g., Mary, 3) • Can’t directly talk about properties of individuals or relations between individuals (e.g., “Bill is tall”) • Generalizations, patterns, regularities can’t easily be represented (e.g., “all triangles have 3 sides”) • First-Order Logic (abbreviated FOL or FOPC) is expressive enough to concisely represent this kind of information FOL adds relations, variables, and quantifiers, e.g., •“Every elephant is gray”: x (elephant(x) → gray(x)) •“There is a white alligator”: x (alligator(X) ^ white(X))
- 20. 20 Example • Consider the problem of representing the following information: – Every person is mortal. – Confucius is a person. – Confucius is mortal. • How can these sentences be represented so that we can infer the third sentence from the first two?
- 21. 21 Example II • In PL we have to create propositional symbols to stand for all or part of each sentence. For example, we might have: P = “person”; Q = “mortal”; R = “Confucius” • so the above 3 sentences are represented as: P Q; R P; R Q • Although the third sentence is entailed by the first two, we needed an explicit symbol, R, to represent an individual, Confucius, who is a member of the classes “person” and “mortal” • To represent other individuals we must introduce separate symbols for each one, with some way to represent the fact that all individuals who are “people” are also “mortal”
- 22. 22 The “Hunt the Wumpus” agent • Some atomic propositions: S12 = There is a stench in cell (1,2) B34 = There is a breeze in cell (3,4) W22 = The Wumpus is in cell (2,2) V11 = We have visited cell (1,1) OK11 = Cell (1,1) is safe. etc • Some rules: (R1) S11 W11 W12 W21 (R2) S21 W11 W21 W22 W31 (R3) S12 W11 W12 W22 W13 (R4) S12 W13 W12 W22 W11 etc • Note that the lack of variables requires us to give similar rules for each cell
- 23. 23 After the third move • We can prove that the Wumpus is in (1,3) using the four rules given. • See R&N section 7.5
- 24. 24 Proving W13 • Apply MP with S11 and R1: W11 W12 W21 • Apply And-Elimination to this, yielding 3 sentences: W11, W12, W21 • Apply MP to ~S21 and R2, then apply And-elimination: W22, W21, W31 • Apply MP to S12 and R4 to obtain: W13 W12 W22 W11 • Apply Unit resolution on (W13 W12 W22 W11) and W11: W13 W12 W22 • Apply Unit Resolution with (W13 W12 W22) and W22: W13 W12 • Apply UR with (W13 W12) and W12: W13 • QED
- 25. 25 Problems with the propositional Wumpus hunter • Lack of variables prevents stating more general rules – We need a set of similar rules for each cell • Change of the KB over time is difficult to represent – Standard technique is to index facts with the time when they’re true – This means we have a separate KB for every time point
- 26. 26 Summary • The process of deriving new sentences from old one is called inference. – Sound inference processes derives true conclusions given true premises – Complete inference processes derive all true conclusions from a set of premises • A valid sentence is true in all worlds under all interpretations • If an implication sentence can be shown to be valid, then—given its premise—its consequent can be derived • Different logics make different commitments about what the world is made of and what kind of beliefs we can have regarding the facts – Logics are useful for the commitments they do not make because lack of commitment gives the knowledge base engineer more freedom • Propositional logic commits only to the existence of facts that may or may not be the case in the world being represented – It has a simple syntax and simple semantics. It suffices to illustrate the process of inference – Propositional logic quickly becomes impractical, even for very small worlds