QMC Program: Trends and Advances in Monte Carlo Sampling Algorithms Workshop, Discontinuous Hamiltonian Monte Carlo for Sampling Discrete Parameters - Aki Nishimura, Dec 12, 2017

Discontinuous Hamiltonian Monte Carlo
for discontinuous and discrete distributions
Aki Nishimura
joint work with David Dunson and Jianfeng Lu
SAMSI Workshop: Trends and Advances in Monte Carlo Sampling Algorithms
December 12, 2017

Models with discrete params / discontinuous likelihoods
Discrete : unknown population size, change points
Discontinuous : nonparametric generalized Bayes, threshold eﬀects

Hamiltonian Monte Carlo (HMC) for Bayesian computation
Bayesian inference often relies on Markov chain Monte Carlo.
HMC has become popular as an eﬃcient general-purpose algorithm:
allows for more ﬂexible generative models (e.g. non-conjugacy).
a critical building block of probabilistic programming languages.

Idea of a probabilistic programming language: you specify the model,
then the software takes care of the rest.

Probabilistic programming languages can algorithmically evaluate
(unnormalized) log posterior density.
(unnormalized) log conditional densities eﬃciently by taking
advantage of conditional independence structure.
gradients of log density.

Probabilistic programming languages can algorithmically evaluate
(unnormalized) log posterior density.
(unnormalized) log conditional densities eﬃciently by taking
advantage of conditional independence structure.
gradients of log density.
HMC is well-suited to such softwares and has demonstrated
a number of empirical successes e.g. through Stan and PyMC.
better theoretical scalability in the number of parameters
(Beskos et al., 2013).

HMC and discrete parameters / discontinuous likelihoods
HMC is based on solutions of an ordinary diﬀerential equation.
But the ODE makes no sense for discrete parameters / discontinuous
likelihoods.

likelihoods.
HMC’s inability to handle discrete parameters is considered the most
serious drawback (Gelman et al., 2015; Monnahan et al., 2016).

likelihoods.
HMC’s inability to handle discrete parameters is considered the most
serious drawback (Gelman et al., 2015; Monnahan et al., 2016).
Existing approaches in special cases:
smooth surrogate function for binary pairwise Markov random
ﬁeld models (Zhang et al., 2012).
treat discrete parameters as continuous if the likelihood still
makes sense (Berger et al., 2012).

Our approach: discontinous HMC
Features:
allows for a discontinuous target distribution.
handles discrete parameters through embedding them into a
continuous space.
ﬁts within the framework of probabilistic programming languages.

Features:
continuous space.
Techniques:
is motivated by theory of measure-valued diﬀerential equation &
event-driven Monte Carlo.
is based on a novel numerical method for discontinuous dynamics.

Features:
continuous space.
Techniques:
is motivated by theory of measure-valued diﬀerential equation &
event-driven Monte Carlo.
is based on a novel numerical method for discontinuous dynamics.
Theoretical properties:
generalizes (and hence outperforms) variable-at-a-time Metropolis.
achieves a high acceptance rate that indicates a scaling property
comparable to HMC.

Review of HMC
Table of Contents
1 Review of HMC
2 Turning discrete problems into discontinuous ones
3 Theory of discontinuous Hamiltonian dynamics
4 Numerical method for discontinuous dynamics
5 Numerical results
6 Results

Review of HMC
HMC in its basic form
HMC samples from an augmented parameter space (θ, p) where:
π(θ, p) ∝ πΘ(θ) × N (p ; 0, mI)
U(θ) = − log πΘ(θ) is called potential energy.

Review of HMC
π(θ, p) ∝ πΘ(θ) × N (p ; 0, mI)
Transition rule of HMC
Given the current state (θ0, p0), HMC generates the next state as follows:
1 Re-sample p0 ∼ N (0, mI)
2 Generate a Metropolis proposal by solving Hamilton’s equation:
dθ
dt
= m−1
p,
dp
dt
= − θU(θ) (1)
with the initial condition (θ0, p0).
3 Accept or reject the proposal.

Review of HMC
π(θ, p) ∝ πΘ(θ) × N (p ; 0, mI)
1 Re-sample p0 ∼ N (0, mI)
dθ
dt
= m−1
p,
dp
dt
= − θU(θ) (1)
Interpretation of (1): dθ
dt = velocity, mass × d
dt (velocity) = − θU(θ)

Review of HMC
Visual illustration: HMC in action
HMC for a 2d Gaussian (correlation = 0.9)

Review of HMC
HMC in a more general form
π(θ, p) ∝ πΘ(θ) × πP (p)
K(p) = − log πP (p) is called kinetic energy.
1 Re-sample p0 ∼ πP (·).
dθ
dt
= pK(p)
dp
dt
= − θU(θ) (2)

Review of HMC
Properties of Hamiltonian dynamics
Conservation of energy:
U(θ(t)) + K(p(t)) = U(θ0) + K(p0) for all t ∈ R
a basis for high acceptance probabilities of HMC proposals.

Review of HMC
Properties of Hamiltonian dynamics
Conservation of energy:
U(θ(t)) + K(p(t)) = U(θ0) + K(p0) for all t ∈ R
a basis for high acceptance probabilities of HMC proposals.
Reversibility & Volume-preservation
symmetry of proposals “P(x → x∗) = P(x∗ → x)”

Turning discrete problems into discontinuous ones
Table of Contents
1 Review of HMC
5 Numerical results
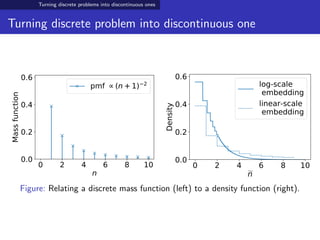
6 Results

Turning discrete problem into discontinuous one
Consider a discrete parameter N ∈ Z+ with a prior πN (·).
Map N into a continuous parameter N such that
N = n if and only if N ∈ (an, an+1]
To match the distribution of N, the corresponding density of N is
πN
(˜n) =
n≥1
πN (n)
an+1 − an
1{an < ˜n ≤ an+1}

Turning discrete problem into discontinuous one
0 2 4 6 8 10
n
0.0
0.2
0.4
0.6
Massfunction
pmf (n+1) 2
0 2 4 6 8 10
n
0.0
0.2
0.4
0.6
Density
log-scale
embedding
linear-scale
embedding
Figure: Relating a discrete mass function (left) to a density function (right).

What about more complex discrete spaces?
Graphs? Trees?
For “momentum” to be useful, we need a notion of direction.

What about more complex discrete spaces?
Short answer: I don’t know. (Let me know if you got ideas.)
Graphs? Trees?
For “momentum” to be useful, we need a notion of direction.

Theory of discontinuous Hamiltonian dynamics
Table of Contents
1 Review of HMC
5 Numerical results
6 Results

When U(θ) = − log π(θ) is discontinuous, Hamilton’s equations
dθ
dt
= pK(p)
dp
dt
= − θU(θ) (3)
becomes a measure-valued diﬀerential equation / inclusion.
θi
U(θ)
Figure:

Deﬁne discontinuous dynamics as a limit of smooth dynamics:
Uδ — smooth approximations of U i.e. limδ→0 Uδ = U.
(θδ, pδ)(t) — the solution corresponding to Uδ.
θi
U(θ)
Uδ(θ)
Figure:

Deﬁne discontinuous dynamics as a limit of smooth dynamics:
Uδ — smooth approximations of U i.e. limδ→0 Uδ = U.
(θδ, pδ)(t) — the solution corresponding to Uδ.
(θ, p)(t) := limδ→0(θδ, pδ)(t).
θi
U(θ)
Uδ(θ)
Figure: Example trajectory θ(t) of discontinuous Hamiltonian dynamics.

Behavior of dynamics at discontinuity
When the trajectory θ(t) encounters a discontinuity of U at event
time te, the momentum p(t) undergoes an instantaneous change.

The change in p occurs only in the direction of “− θU(θ)”:
p(t+
e ) = p(t−
e ) − γ ν (θ(te))
where ν(θ) is orthonormal to the discontinuity boundary of U.

The change in p occurs only in the direction of “− θU(θ)”:
p(t+
e ) = p(t−
e ) − γ ν (θ(te))
where ν(θ) is orthonormal to the discontinuity boundary of U.
The scalar γ is determined by the energy conservation principle:
K(p(t+
e )) − K(p(t−
e )) = U(θ(t−
e )) − U(θ(t+
e ))
(provided K(p) is convex and K(p) → ∞ as p → ∞).

Numerical method for discontinuous dynamics
Table of Contents
1 Review of HMC
5 Numerical results
6 Results

Dealing with discontinuity

How about ignoring them?

How about ignoring them?
Leapfrog integrator completely fails to preserve the energy.
i.e. low (or even negligible) acceptance probabilities.

Event-driven approach at discontinuity
Pakman and Paninski (2013) and Afshar and Domke (2015):
Detect discontinuities and treat them appropriately.
(Event-driven Monte Carlo of Alder and Wainwright (1959).)

Event-driven approach at discontinuity
Pakman and Paninski (2013) and Afshar and Domke (2015):
Detect discontinuities and treat them appropriately.
(Event-driven Monte Carlo of Alder and Wainwright (1959).)
Problem: in Gaussian momentum case, the change in U(θ) must be
computed across every single discontinuity.

Problem with Gaussian momentum & existing approach
Say var(N) ≈ 1, 000. Then a Metropolis step N → N ± 1, 000
should have a good chance of acceptance.
The numerical method requires 1, 000 density evaluations (ouch!)
for a corresponding transition.
ΔU ≈ .01
Figure: Conditional distribution of an embedded discrete parameter in
the Jolly-Seber example.

Laplace momentum: better alternative
Consider a Laplace momentum π(p) ∝ i exp(−m−1
i |pi|).
The corresponding Hamilton’s equation is
dθ
dt
= m−1
· sign(p),
dp
dt
= − θU(θ)

Laplace momentum: better alternative
Consider a Laplace momentum π(p) ∝ i exp(−m−1
i |pi|).
The corresponding Hamilton’s equation is
dθ
dt
= m−1
· sign(p),
dp
dt
= − θU(θ)
Key property: the velocity dθ/dt depends only on the signs of pi’s
and not on their magnitudes.
This property allows an accurate numerical approximation
without keeping track of small changes in pi’s.

Numerical method for Laplace momentum
Observation: approximating dynamics based on Laplace momentum is
simple in a 1-D case — dθ/dt = m−1 sign(p), dp/dt = − U(θ)
θ θ* = θ + Δt × m-1 sign(p)
U(θ)
p

U(θ)
p U(θ*) − U(θ) < K(p) ?

U(θ)
U(θ*) − U(θ) = K(p) − K(p*)
p*

θ θ*
U(θ*) − U(θ)
p

p* ← - p
θ* ← θ

Coordinate-wise integration for Laplace momentum
For θ ∈ Rd, we can split the ODE into its coordinate-wise component:
dθi
dt
= m−1
i sign(pi),
dpi
dt
= −∂θi
U(θ),
dθ−i
dt
=
dp−i
dt
= 0 (4)

4 2 0 2
4
2
0
2
4
0
1
2
3
4
5
Figure: Trajectory of a numerical solution via the coordinate-wise integrator.

Reversibility preserved by symmetric splitting or randomly permuting
the coordinates.
We can also use Laplace momentum for discrete parameters and
Gaussian momentum for continuous parameters.

Properties of discontinuous HMC
When using independent Laplace momentum,
Proposals are rejection-free thanks to exact energy conservation.1
1
But too big of a stepsize leads to poor mixing.

Taking one numerical integration step of DHMC
≡
Variable-at-a-time Metropolis.
1

Taking one numerical integration step of DHMC
≡
Variable-at-a-time Metropolis.
When mixing Laplace and Gaussian momentum:
Errors in energy is O(∆t2), and hence 1 − O(∆t4) acceptance rate.
1

Numerical results
Table of Contents
1 Review of HMC
5 Numerical results
6 Results

Numerical results
Numerical results: Jolly-Seber (capture-recapture) model
Data : the number of marked / unmarked individuals over multiple
capture occasions
Parameters : population sizes, capture probabilities, survival rates

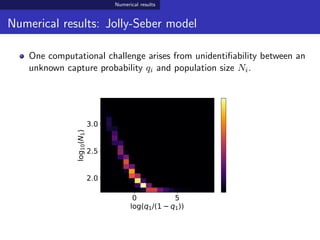
Numerical results
Numerical results: Jolly-Seber model
One computational challenge arises from unidentiﬁability between an
unknown capture probability qi and population size Ni.
0 5
log(q1/(1 q1))
2.0
2.5
3.0
log10(N1)

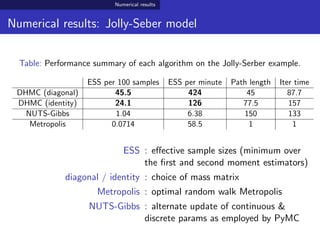
Numerical results
Numerical results: Jolly-Seber model
Table: Performance summary of each algorithm on the Jolly-Serber example.
ESS per 100 samples ESS per minute Path length Iter time
DHMC (diagonal) 45.5 424 45 87.7
DHMC (identity) 24.1 126 77.5 157
NUTS-Gibbs 1.04 6.38 150 133
Metropolis 0.0714 58.5 1 1
ESS : eﬀective sample sizes (minimum over
the ﬁrst and second moment estimators)
diagonal / identity : choice of mass matrix
Metropolis : optimal random walk Metropolis
NUTS-Gibbs : alternate update of continuous &
discrete params as employed by PyMC

Numerical results
Numerical results: generalized Bayesian inference
For a given loss function (y, θ) of interest, a generalized posterior
(Bissiri et al., 2016) is given by
πpost(θ) ∝ exp − i (yi, θ) πprior(θ)
We consider a binary classiﬁcation with the 0-1 loss
(y, θ) = 1{y = sign(x θ)} for y ∈ {−1, 1}.

Numerical results
For a given loss function (y, θ) of interest, a generalized posterior
(Bissiri et al., 2016) is given by
πpost(θ) ∝ exp − i (yi, θ) πprior(θ)
We consider a binary classiﬁcation with the 0-1 loss
(y, θ) = 1{y = sign(x θ)} for y ∈ {−1, 1}.
9.2 9.0 8.8
Intercept
0
2
4
6
Density(conditional)

Numerical results
Data: semiconductor quality with various sensor measurements
Goal: predict faulty products / infer relevant sensor measurements

Numerical results
Table: Performance summary on the generalized Bayesian posterior example.
ESS per 100 samples ESS per minute Path length Iter time
DHMC 26.3 76 25 972
Metropolis 0.00809 (± 0.0018) 0.227 1 1
Variable-at-a-time 0.514 (± 0.039) 39.8 1 36.2
9.2 9.0 8.8
Intercept
0
2
4
6
Density(conditional)

Results
Table of Contents
1 Review of HMC
5 Numerical results
6 Results

Results
Summary
Hamiltonian dynamics based on Laplace momentum allows an
eﬃcient exploration of discontinuous target distributions.
Numerical method with exact energy conservation property.

Results
Future directions
Test DHMC on a wider range of applications in the context of a
probabilistic programming language.
Explore the utility of Laplace momentum as an alternative to
Gaussian one.
What to do with more complex discrete spaces?
Develop notion of directions.
Avoid rejections by “swapping” probability between θ and p.

Results
References
Nishimura, A., Dunson, D. and Lu, J. (2017) “Discontinuous Hamiltonian
Monte Carlo for sampling discrete parameters,” arXiv:1705.08510.
Code available at
https://github.com/aki-nishimura/discontinuous-hmc

QMC Program: Trends and Advances in Monte Carlo Sampling Algorithms Workshop, Discontinuous Hamiltonian Monte Carlo for Sampling Discrete Parameters - Aki Nishimura, Dec 12, 2017

More Related Content

What's hot (20)

Similar to QMC Program: Trends and Advances in Monte Carlo Sampling Algorithms Workshop, Discontinuous Hamiltonian Monte Carlo for Sampling Discrete Parameters - Aki Nishimura, Dec 12, 2017 (20)

More from The Statistical and Applied Mathematical Sciences Institute (20)

Recently uploaded (20)

QMC Program: Trends and Advances in Monte Carlo Sampling Algorithms Workshop, Discontinuous Hamiltonian Monte Carlo for Sampling Discrete Parameters - Aki Nishimura, Dec 12, 2017