Quantitative Methods for Lawyers - Class #19 - Regression Analysis - Part 2
1 like2,009 views
This document summarizes key concepts from a lecture on regression analysis: 1) Regression analysis estimates the relationship between variables and the effect of changing one variable over another, assuming a linear relationship and additive effects. 2) Bivariate regression on SAT scores and education expenditures in U.S. states found a negative relationship, unlike initial assumptions. 3) Multivariate regression controls for multiple predictor variables simultaneously to better estimate relationships between variables like SAT scores and expenditures.
Quantitative Methods for Lawyers - Class #19 - Regression Analysis - Part 2
- 1. Quantitative Methods for Lawyers Class #19 Regression Analysis Part 2 + 25.39* 1 if region3=true @ computational computationallegalstudies.com professor daniel martin katz danielmartinkatz.com lexpredict.com slideshare.net/DanielKatz
- 2. “We use regression to estimate the unknown effect of changing one variable over another regression requires making two assumptions: 1) there is a linear relationship between two variables (i.e. X and Y) 2) this relationship is additive (i.e. Y= X1 + X2 + ...+ Xn) (Note: Additivity applies across terms - as within terms there can be a square, log, etc.) Technically, linear regression estimates how much Y changes when X changes one unit.” http://dss.princeton.edu/training/ Regression Analysis
- 3. Example: After controlling by other factors, are SAT scores higher in states that spend more money on education?* Outcome (Y) variable = SAT scores --> variable csat in dataset Predictor (X) variables • Per Pupil Expenditures Primary & Secondary (expense) • % HS of graduates taking SAT (percent) • Median Household Income (income) • % adults with HS Diploma (high) • % adults with College Degree (college) • Region (region) Regression Analysis *Source: search for dataset at http://www.duxbury.com/highered/ Use the file states.dta (educational data for the U.S.).
- 4. Getting Started Lets Begin by Loading it and Use the Head Command https://s3.amazonaws.com/KatzCloud/states.dta
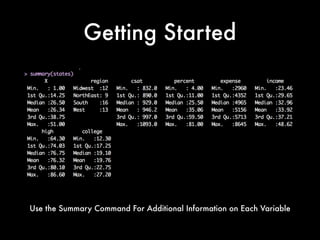
- 5. Getting Started Use the Summary Command For Additional Information on Each Variable
- 6. Bivariate Regression Example Lets Start Simple: We Might Hypothesize a Positive Relationship As Expenditures Go Up SAT Performances Also Goes Up Relationship Between Sat Score and Expenditures?
- 7. Bivariate Regression Example It is Certainly NOT Definitive But a Scatterplot is a good place to start ...
- 8. Notice the Nature of the Relationship is not what we would naively anticipate It is Certainly NOT Definitive But a Scatterplot is a good place to start ... Bivariate Regression Example
- 9. It Appears to be a Negative Relationship Notice the Nature of the Relationship is not what we would naively anticipate It is Certainly NOT Definitive But a Scatterplot is a good place to start ... Bivariate Regression Example
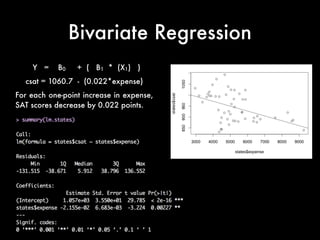
- 10. Bivariate Regression Notice the -.02155 for expense which is the slope of the regression line shown above w e j u s t fi t t h e regression line to this bivariate relationship
- 11. Bivariate Regression Y = B0 + ( B1 * (X1) ) csat = 1060.7 - (0.022*expense) For each one-point increase in expense, SAT scores decrease by 0.022 points.
- 12. Bivariate Regression Y = B0 + ( B1 * (X1) ) csat = 1060.7 - (0.022*expense) Look at the T Stats, P Values with a Tstat (which is Z when N>30) of Greater than 1.96 we can reject the notion that the coefficient is equal to zero
- 13. A Brief Word about Standard Errors N o t i c e t h a t t h e 9 5 % Confidence Interval is the Beta Coefficient ~ Plus or Minus Two Times the Standard Error The standard error of the estimate tells us the accuracy to expect from our prediction -- The standard error of a correlation coefficient is used to determine the confidence intervals around a true correlation of zero. look at the Standard Error and you can obtain the 95% Confidence Interval 1057 + 2(35.5) = ~1127 1057 - 2(35.5) = ~ 987.0
- 15. Now Lets Consider the More Complex Case: Relationship Between Sat Score and Expenditures/ Variety of other Variables ? Our Y Dependent Variable Our X Predictors/ Independent Variables Multivariate Regression
- 16. Y = B0 + ( B1 * (X1) ) – ( B2 * (X2) ) + ( B3 * (X3) ) + ( B4 * (X4)) + ( B5 * (X5) ) + ε csat = 851.56 + 0.003*expense – 2.62*percent + 0.11*income + 1.63*high + 2.03*college + ε
- 17. Lets Consider Our “Beta Coefficients” Are They Statistically Significant? Look at the P Value on “Expense” - It is no longer Statistically Significant
- 18. Two Ways to Think About Significance: Is the P Value > .05? Is the Tstat < 1.96? Variable Significant @ .05 Level expense no percent yes income no high no college no intercept yes
- 19. Using Our Model to Predict
- 20. Using Our Model to Predict csat = 851.56 + 0.003*expense – 2.62*percent + 0.11*income + 1.63*high + 2.03*college + ε Here is our Model:
- 21. Using Our Model to Predict csat = 851.56 + 0.003*expense – 2.62*percent + 0.11*income + 1.63*high + 2.03*college + ε What if we had a Hypothetical State with the following factors - • Per Pupil Expenditures Primary & Secondary (expense) - $6000 • % HS of graduates taking SAT (percent) - 20% • Median Household Income (income) - 33.000 • % adults with HS Diploma (high) - 70% • % adults with College Degree (college) - 15% Here is our Model:
- 22. Using Our Model to Predict csat = 851.56 + 0.003*expense – 2.62*percent + 0.11*income + 1.63*high + 2.03*college + ε What if we had a Hypothetical State with the following factors - • Per Pupil Expenditures Primary & Secondary (expense) - $6000 • % HS of graduates taking SAT (percent) - 20% • Median Household Income (income) - 33.000 • % adults with HS Diploma (high) - 70% • % adults with College Degree (college) - 15% csat = 851.56 + 0.003*(6000) – 2.62*(20) + 0.11*(33.000) + 1.63*(70) + 2.03*(15) + ε Here is the Predicted SAT SCORE for that STATE: csat = 851.56 + 18 – 52.4 + 3.63 + 114.1 + 30.45 + ε csat = 965.34 Here is our Model:
- 23. Goodness of Fit
- 24. Goodness of Fit We want to have an idea of how well our regression line fits the data When we have 1 Independent Variables we are fitting in 2 Dimensional Space 2 Independent Variables we are fitting in 3 Dimensional Space 3 Independent Variables is a 4D Space Etc. Note:
- 25. Goodness of Fit Lets look at the correlation structure First need to do something with this non-numeric column
- 26. Goodness of Fit Lets look at the correlation structure Need to do something with this non-numeric column create new version
- 27. Goodness of Fit Lets look at the correlation structure Need to do something with this non-numeric column remove the region column create new version
- 28. Goodness of Fit Lets look at the correlation structure Need to do something with this non-numeric column okay all set remove the region column create new version
- 29. Goodness of Fit Lets look at the correlation structure -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 csat percent expense income high college -0.88 -0.47 -0.47 0.09 -0.37 0.65 0.67 0.14 0.61 0.68 0.31 0.64 0.51 0.72 0.53 1 -0.88 -0.47 -0.47 0.09 -0.37 1 0.65 0.67 0.14 0.61 1 0.68 0.31 0.64 1 0.51 0.72 1 0.53 1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1csat percent expense income high college csat percent expense income high college
- 30. Goodness of Fit In the 2 Dimensional Case - the R Squared is Square of the Correlation Coefficient (-0.4663)^2 = 0.2174
- 31. Goodness of Fit These Help Us Understand the overall fit of the model It is the proportion of variability in a data set that is accounted for by the statistical model. Okay Now Check Out the Multiple Regression Case: R-Squared Adjusted R-Squared
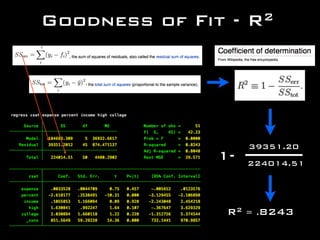
- 32. Goodness of Fit - R2 1- 39351.20 224014.51 R2 = .8243
- 33. Goodness of Fit - The Adjusted R2 R2 = .8243 Adjusted R2 = .8048 Adjusts for the number of predictors in the model and the total sample size http://www.danielsoper.com/ statcalc3/calc.aspx?id=25 Check it out at this website
- 34. Goodness of Fit - R2 In regression, the R2 coefficient of determination is a statistical measure of how well the regression line approximates the real data points. An R2 of 1.0 indicates that the regression line perfectly fits the data. R2 Values closer to 1 indicate a model that better fits the data (there are important caveats to this so please tread lightly with respect to R2 ) R2 Values closer to 0 indicate a model that does not fit the data quite as well
- 35. Goodness of Fit - R2 R² does not indicate whether: * the independent variables are a true cause of the changes in the dependent variable * omitted-variable bias exists * the correct regression was used * the most appropriate set of independent variables has been chosen * there is collinearity present in the data on the explanatory variables * the model might be improved by using transformed versions of the existing set of independent variables.
- 36. Dummy Variables
- 37. Dummy Variables dummy variable (also known as an indicator variable) is variable that takes the values (0 or 1) to indicate the absence or presence of some categorical effect that may be expected to shift the outcome
- 38. Dummy Variables Region can be separated into 4 dummy Variables. Regions: 1 = West (Base Case) 2 = N. East 3 = South 4 = Midwest
- 40. Recoding Dummy Variables okay but we need to pass these results into something
- 41. Recoding Dummy Variables this will take care of that for you now we need to bind the two together and pass the result into a new data set called “states3” lets take a look at the results ....
- 42. Recoding Dummy Variables okay looks good!
- 43. Dummy Variables
- 44. Dummy Variables Region can be separated into 4 dummy Variables. Regions: 1 = West (Base Case) 2 = N. East 3 = South 4 = Midwest Y = B0 + ( B1 * (X1) ) – ( B2 * (X2) ) + ( B3 * (X3) ) + ( B4 * (X4)) + ( B5 * (X5) ) + ( B6 * (X6) ) + ( B7 * (X7) ) + ( B8 * (X8) ) + ε csat = 842.59 – 0.002*expense – 3.01*percent – 0.17*income + 1.81*high + 4.67*college + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε
- 45. Dummy Variables Take a Look if Region = than the last 3 terms will be turned off Think of Dummy Variables as Light Switches when they are on than the associated beta coefficient is on Y = B0 + ( B1 * (X1) ) – ( B2 * (X2) ) + ( B3 * (X3) ) + ( B4 * (X4)) + ( B5 * (X5) ) + ( B6 * (X6) ) + ( B7 * (X7) ) + ( B8 * (X8) ) + ε csat = 842.59 – 0.002*expense – 3.01*percent – 0.17*income + 1.81*high + 4.67*college + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε
- 46. Using Our Model to Predict
- 47. Using Our Model to Predict What if we had a Hypothetical State with the following factors - • Per Pupil Expenditures Primary & Secondary (expense) - $6000 • % HS of graduates taking SAT (percent) - 20% • Median Household Income (income) - 33.000 • % adults with HS Diploma (high) - 70% • % adults with College Degree (college) - 15% • Midwest State (Region=South) Please Predict the Mean Score for this Hypothetical State? Here is our Model: csat = 849.59 – 0.002*expense – 3.01*percent – 0.17*income + 1.81*high + 4.67*college + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε
- 48. Using Our Model to Predict What if we had a Hypothetical State with the following factors - • Per Pupil Expenditures Primary & Secondary (expense) - $6000 • % HS of graduates taking SAT (percent) - 20% • Median Household Income (income) - 33.000 • % adults with HS Diploma (high) - 70% • % adults with College Degree (college) - 15% • Midwest State (Region=South) Here is our Model: csat = 849.59 – 0.002*expense – 3.01*percent – 0.17*income + 1.81*high + 4.67*college + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε csat = 849.59 – 0.002*(6000) – 3.01*(20) – 0.17*(33.000) + 1.81*(70) + 4.67*(15) + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε
- 49. Using Our Model to Predict csat = 849.59 – 0.002*(6000) – 3.01*(20) – 0.17*(33.000) + 1.81*(70) + 4.67*(15) + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε csat = 849.59 – 0.002*expense – 3.01*percent – 0.17*income + 1.81*high + 4.67*college + -34.57*1 if regionWest=true + 34.87* 1 if regionNorthEast=true - 9.18* 1 if regionSouth=true + ε csat = 849.59 – 12 – 60.2 – 5.61 + 126.7 + 70.05 + - 9.18 predicted composite SAT Score = 959.35
- 50. Daniel Martin Katz @ computational computationallegalstudies.com lexpredict.com danielmartinkatz.com illinois tech - chicago kent college of law@