Solved problems pipe flow final 1.doc

Pipes and Multi Pipe Systems 1
P
Pi
ip
pe
es
sa
an
nd
dM
Mu
ul
lt
ti
iP
Pi
ip
pe
e
S
Sy
ys
st
te
em
ms
s

(
(W
Wo
or
rk
ke
ed
d
E
Ex
xa
am
mp
pl
le
es
s)
)

Worked Example (1)
Two pipes of identical diameter and material are connected in parallel.
The length of pipe A is twice the length of pipe B. Assuming the flow is
fully turbulent in both pipes and thus the friction factor is independent of
the Reynolds number and disregarding minor losses, Determine the ratio
of the flow rates in the two pipes.
f1 & D1 & L1 & V1
f2 & D2 & L2 & V2
Pipe 
Pipe 
Q1
Q2
Qt
A B
Solution
For a system of two parallel pipes  and  between junctions A and B
with negligible minor losses, the head losses in each individual pipe
must be the same and can be expressed as
)
2
(
)
1
( L
L h
h  or

















g
2
V
D
l
f
g
2
V
D
l
f 2
2
2
2
2
2
1
1
1
1
The ratio of the average velocities and flow rates becomes
2
/
1
2
1
1
2
1
2
2
1
D
D
.
l
l
.
f
f
V
V








 and
2
/
1
2
1
1
2
1
2
2
2
2
1
2
2
1
1
2
1
D
D
.
l
l
.
f
f
D
D
V
A
V
A
Q
Q










 ……. (1)

In the case of two identical pipes ( 2
1
2
1 D
D
,
f
f 
 ) and 1
2 2l
l  with
canceling the common factors and rearranging Eq. (1) becomes
2
2
2
1 Q
2
Q 
or
The ratio of the flow rates in the two pipes 707
.
0
2
Q
Q
2
1


Worked Example (2)
Two pipes are connected in parallel. One pipe is twice the diameter of
the other and three times as long. Assume that f in the large pipe is 0.02
and f in the smaller one is 0.013. Determine the ratio of the discharge in
the two pipes.
Solution:
For pipes in parallel,
)
2
(
L
)
1
(
L
B
A
L h
h
h 

 
Using Darcy- Weisbach equation
2
2
1
2
g
2
V
D
L
f
g
2
V
D
L
f

















………………………………………… (1)
Substituting the mean velocity A
Q
V  and rearranging
5
2
1
1
2
1
2
2
1
D
D
L
L
f
f
Q
Q










 …………………………………………(2)

For the given data, 02
.
0
f
,
D
2
D
,
L
3
L 1
2
1
2
1 

 and 013
.
0
f2  Eq. (2)
gives
63
.
2
D
D
2
L
3
L
02
.
0
013
.
0
Q
Q
5
2
2
2
2
2
1












Worked Example (3)
A pipe line 76cm in diameter and 6.44km long delivers 0.56m3
/s; f =
0.024;
¤ Find the loss of pressure due to friction.
¤ If the last half of the pipe is replaced by two 61cm dia. pipes in
parallel, what will be the total loss of head for the same total
delivery?
¤ What will be the delivery if the original friction loss is
permitted? Neglect minor losses.
Solution
Case (a): The total head losses across the system is
g
2
V
D
L
f
h
2
L 

 …………………………….. (1)
Since there is no change in the piping system, the velocity is constant
and can be determined using the continuity relation as
4
/
D
Q
V 2



Head losses can be expressed in terms of flow rate through Darcy-
Weisbach (Eq. 1) as
2
5
2
2
2
L Q
D
1
.
12
L
f
4
/
D
Q
D
L
f
g
2
V
D
L
f
h 














(for SI system) ………. (2)
(D and L are in m, Q is in m3
/s, and f is dimensionless)
Substituting the data of the given system (D = 0.76m, L = 6.44103
m
and f = 0.024) into Eq. (2) gives
m
80
.
15
56
.
0
)
76
.
0
(
1
.
12
10
44
.
6
024
.
0
h 2
5
3
L 




 
Case (b): To calculate the total loss of head for the same total delivery
and the last half of the pipe is replaced by two 61cm dia.
pipes in parallel
If the last half of the pipe is replaced by two 61cm dia. pipes in parallel,
the head loss hL,2 from J to B is the same as that from J to C.
Since the total water delivery (Q =0.56m3
/s) is the same and the pipe
(pipe 1) has the same properties
m
90
.
7
2
/
8
.
15
h 1
,
L 


L1 = 3.22 km &
D1 = 0.76 m & f1 = 0.024
V1
V2
L3 = 3.22 km &
D3 = 0. 61 m & f3 = 0.024


hL1
hL2
EGL
HGL
J
L2 = 3.22 km &
D2 = 0. 61 m & f2 = 0.024
A
B
C
V2
V2
and 3
L
2
L h
h  for the two identical pipes JB & JC (f2 = f3 , L2 = L3 and
D2 = D3) which can be calculated as
m
93
.
5
)
2
/
56
.
0
(
)
61
.
0
(
1
.
12
10
22
.
3
024
.
0
Q
D
1
.
12
L
f
h 2
5
3
2
5
2
L 







(Note: Q2 = Q3 = 0.56 / 2 m3
/s)
Thus, the total loss of head for the same total delivery
m
83
.
13
93
.
5
90
.
7
h
h
h 2
L
1
L
L 




 ………………….. (3)
Case (c): To calculate the delivery if the original friction loss is
permitted

L1 = 3.22 km &
D1 = 0.76 m & f1 = 0.024
Q
Q / 2
L3 = 3.22 km &
D3 = 0. 61 m & f3 = 0.024


hL1
hL2
EGL
HGL
J
Q / 2
L2 = 3.22 km &
D2 = 0. 61 m & f2 = 0.024
A
B
C
m
8
15
h
h 2
L
1
L .



15.80m
Since the two parallel pipes JB and JC are identically; Q2 = Q3 = Q / 2.
For the given pipe system with negligible minor losses, the head
losses for the two pipes in series AJ and JB (or AJ and JC) are
expressed in the given identical equations:
2
L
1
L
L h
h
h 

 …………………………….. (4.a)
3
L
1
L
L h
h
h 

 …………………………….. (4.b)
Substituting in Eq. (4.a) gives

















5
2
5
2
3
2
2
5
2
2
2
2
1
5
1
1
1
L
61
.
0
4
/
Q
76
.
0
Q
1
.
12
10
22
.
3
024
.
0
Q
D
1
.
12
L
f
Q
D
1
.
12
L
f
h
.. (5)
For m
8
.
15
hL 
 , solving Eq. (5) for Q gives

s
/
m
60
.
0
90
.
6
47
.
2
Q 3

 
Worked Example (4)
Two reservoirs whose difference of level is m
15 are connected by a
pipe ABC whose highest point B is m
2 below the level in the upper
reservoir A. The portion AB has a diameter of cm
20 and the portion BC
a diameter of cm
15 , the friction factor being the same for both portions
 
025
.
0
f  . The total length of the pipe is km
3 .
Find the maximum allowable length of the portion AB if the pressure
head at B is not to be more than m
2 below atmospheric pressure.
Neglect the secondary losses.

2m
f for both pipes is the same = 0.025
DB = 15 cm
DA = 20 cm
(15.00)
B

(0.00)
AA = 20 cm
A
C
Solution

We choose point  at the free surface of the first reservoir and B at the
point of change. Noting that the fluid at point  is open to the
atmosphere (and thus .
atm
1 P
P  ) and fluid velocity is zero ( 0
V1  ).
The energy equation for a control volume between point  and B is
B
1
B
2
1
2
h
Z
g
2
V
g
P
Z
g
2
V
g
P

























or
B
1
L
2
B
B
B
1 h
g
2
V
g
P
Z
Z 




 ……………………………………………… (1)
Where B
B P
and
V are the average velocity and the pressure at point B.
The head loss in each pipe (pipe A and pipe B) is expressed in terms of
the discharge as
   
B
A
2
2
2
2
B
A
2
2
AB
2
B
A
B
1
L l
Q
46
.
6
Q
2
.
0
81
.
9
l
025
.
0
8
Q
D
g
l
f
8
h 













……………………………….… (2.a)
Similarly,
2
BC
2
2
2
BC
2
2
BC
2
BC
C
B
L
Q
l
2
.
27
Q
15
.
0
81
.
9
l
025
.
0
8
Q
)
D
(
g
l
f
8
h












… (2.b)
Substituting the given values into Eq. (1)

B
A
2
2
2
2
l
Q
46
.
6
2
.
0
4
81
.
9
2
Q
2
2 















or
 
B
A
2
l
46
.
6
64
.
51
Q
0
.
4 


 ………………………………… (3)
Since the diameter of the piping system is different, then the total head
loss between points  and 
C
B
L
B
A
L
total
L
2
1 h
h
h
15
Z
Z 
 




Using the above calculated values of C
B
L
B
A
L h
h 
  , Eq. (2.a) and Eq.
(2.b), Eq. (3) gives
 
B
A
2
l
74
.
20
81600
Q
15 

 …………………………………………… (4)
Solving Eq. (3) and Eq. (4) yields,
m
4
.
1821
79
.
44
/
3
.
81579
l B
A 


i.e. the maximum allowable length of portion “AB” if the pressure
head at B is not to be more than 2m below atmospheric pressure
= 1821.4m

Worked Example (5)
A pipeline conveying water between two reservoirs A and B is of cm
30
and m
370 long. The difference of head between the two surfaces is
m
25
.
4 .
i. Determine the flow rate ( 02
.
0
f  ),
ii. It is required to increase the discharge by 50% by duplicating a
portion of the pip. If the head and friction factor are unchanged
and minor losses are ignored, find the length of the second pipe
which is of the same diameter as the first.
Solution

4m
f = 0.02 & L = 370m & D = 30cm 
Q
o
We choose points  and  at the free surface of the two reservoirs.
The total head loss across the system is
minor
L
major
L
total
L
2
1
L h
h
h
h 


 …………………………………… (1)
Neglecting minor losses, Eq. (1)
m
0
.
4
h
h major
L
2
1
L 



Using Darcy formula, the head loss is related to the total flow rate by
2
5
2
2
1
L Q
D
g
l
f
8
h 


 …………………………………… (2)
or
5
.
0
5
2
2
1
L
l
f
8
D
g
h
Q













…………………………………… (3)
With 02
.
0
f
,
m
370
l
,
m
3
.
0
D 

 and the head loss m
0
.
4
h 2
1
L 
 , Eq.
(3) gives;
  s
/
m
126
.
0
370
02
.
0
8
3
.
0
81
.
9
4
Q 3
5
.
0
5
2
















Duplicating a portion of the pipe
4 m
Q
o /2


Pipe A of L = 370- l
Pipe B, of L = l

Duplicating a portion of the pipe with second one has the same diameter
and friction factor, as shown in the sketch, increases the discharge from
s
/
m
29
.
1 3
to s
/
m
89
.
1
5
.
1
29
.
1 3


Since pipe B and pipe c are identical, the head loss is the same and the
discharge in each branch= s
/
m
0945
.
0
2
/
89
.
1
2
/
Q 3

 .
Neglecting minor losses and substituting into Eq. (2)
 
 
2
B
2
A
5
2
2
1
L Q
l
Q
370
D
g
f
8
h 






 
or
 
 
 
2
2
5
2
0945
.
0
l
189
.
0
370
3
.
0
81
.
9
02
.
0
8
0
.
4 







 
Solving for  gives,
272
027
.
0
88
.
5
22
.
13




Worked Example (6)
This guess gives m
20
.
40
hJ  , which is an acceptable solution.
Hence the discharge from reservoir A towards the junction (QA)
= 0.02826 m3/s is balanced by (QB) = 0.01415 m3/s away from
the junction J to reservoir B and (QC) = 0.01411 m3/s away from
the junction J to reservoir C.

If the water surface elevation in reservoir B is 110 m. What must the
water surface elevation in reservoir A if a flow of 0.03 m3/s is to occur in
the cast iron pipe (f =0.031)? Draw the HGL and the EGL including
relative slope and changes in slope?
Solution
Applying the energy equation between point A and point B (consider all
losses)
B
h
A L 

or
B
h
h
h
h
h
A )
5
(
L
)
4
(
L
)
3
(
L
)
2
(
L
)
1
(
L 




 …………………(1)
Where
3
EGL
Pipe1: L 1 =100 m, D1 =20 cm
Pipe2: L2 =150 m, D 2=15
cm
 B
 A
5
4
2
1
Q1 Q2

)
1
(
L
h
= inlet
losses
)
2
(
L
h
= friction
losses
)
3
(
L
h
= Sudden
Contr. losses
)
4
(
L
h
= friction
losses
)
5
(
L
h
= exit
losses
g
2
/
V
5
.
0 2
1
g
2
V
D
L
f
2
1
1
1
1   g
2
V
V 2
1
2 
g
2
V
D
L
f
2
2
2
2
2 g
2
V2
2
For the given data: cm
15
D
and
,
cm
20
D
,
s
/
m
03
.
0
Q 2
1
3


 the
continuity equation gives
  s
/
m
95
.
0
4
/
2
.
0
03
.
0
A
Q
V 2
1
1 




and
  s
/
m
70
.
1
4
/
15
.
0
03
.
0
A
Q
V 2
2
2 




Thus,
  m
02
.
0
81
.
9
2
95
.
0
5
.
0
g
2
V
5
.
0
h 2
2
1
)
1
(
L 



 ………………..… (2)
m
713
.
0
81
.
9
2
95
.
0
2
.
0
100
031
.
0
g
2
V
D
L
f
h
2
2
1
1
1
)
2
(
L 




 ………………… (3)
    m
028
.
0
81
.
9
2
95
.
0
7
.
1
g
2
V
V
h
2
2
2
1
)
3
(
L 




 ………………… (4)
m
566
.
4
81
.
9
2
70
.
1
15
.
0
150
031
.
0
g
2
V
D
L
f
h
2
2
2
2
2
)
4
(
L 




 ………….…… (5)
  m
147
.
0
81
.
9
2
70
.
1
g
2
V
h 2
2
2
)
5
(
L 


 ………………… (6)
Substituting the calculated values into Eq. (1)
m
47
.
115
110
147
.
0
566
.
4
028
.
0
713
.
0
02
.
0
A 







The water surface elevation in tank “A” must be = 115.5 m
Worked Example (7)
Water flows from reservoir  to reservoir  through a cm
30 diameter,
m
200 long pipeline as shown in the figure. The reservoir  surface
elevation is m
100 and reservoir  surface elevation is m
85 . Consider
the minor losses due to the sharp edged entrance (k=0.50), the global
valve (k=10), the two bends (k=0.30), and the sharp edged exit (k=0.50).
The pipeline is galvanized iron with 017
.
0
f  . Determine the discharge
from reservoir  to reservoir.
Solution
Application of the energy equation between points  and  gives
B
A
L
B
2
B
B
A
2
A
A h
g
P
g
2
V
Z
g
P
g
2
V
Z 
























 
 

15 m
2 elbows
Global valve
water

Thus, with 0
P
P
P
,
m
85
Z
,
m
100
Z atm
B
A
B
A 



 (large open tanks).
In addition we assume 0
V
V B
A 

 



 B
A
L
B
A h
85
100
Z
Z ………………………………………… (1)


 

 losses
Minor
losses
Main
h B
A
L
The diameter of the main pipe is constant with a mean velocity VP= Q/A.
Then, and the minor losses
 
g
2
V
k
k
k
2
k
losses
Minor
2
P
exit
valve
elbow
enter 



 ……………………… (2)
Substituting the given value for this condition
 
g
2
V
6
.
11
g
2
V
5
.
0
10
3
.
0
2
5
.
0
losses
Minor
2
P
2
P






 ………………… (3)
For a pipe of 200m long, 0.30m diameter and friction factor f=0.017, the
main losses (friction losses) are
g
2
V
33
.
11
g
2
V
3
.
0
200
017
.
0
g
2
V
D
l
f
losses
Main
2
P
2
P
2
P





 ………………… (4)
With the calculated head losses (Eq. 2 and 3), Eq. (1) gives
 
g
2
V
33
.
11
60
.
11
85
100
Z
Z
2
P
B
A 



 ………………… (5)
or
s
/
m
58
.
3
93
.
22
81
.
9
2
15
VP 




The discharge through the pipe from reservoir  to reservoir 
s
/
lit
253
s
/
m
253
.
0
3
.
0
4
58
.
3
A
V
Q 3
2
P
P 












Worked Example (8)
A certain part of cast iron )
0315
.
0
f
(  piping of a water distribution
system involves a parallel section. Both parallel pipes have a diameter of
cm
30 , and the flow is fully turbulent. One of the branches (Pipe A) is
m
1000 long while the other branch (pipe B) is m
3000 long. If the flow
rate through A is s
/
m
4
.
0 3
, determine the flow rate through pipe B.
s
/
m
40
.
0
Q
and
m
1000
L
,
cm
30
D
:
A
pipe 3



m
3000
L
,
cm
30
D
:
B
pipe 

Solution
For pipes in parallel,
)
B
(
L
)
A
(
L
2
1
L h
h
h 

 
Using Darcy- Weisbach equation
B
2
A
2
g
2
V
D
L
f
g
2
V
D
L
f


















 ………………………………………… (1)
Substituting the mean velocity A
Q
V  and rearranging

5
2
1
1
2
1
2
2
1
D
D
L
L
f
f
Q
Q










 ………………………………………… (2)
For the given data,
s
/
m
40
.
0
Q
,
f
f
,
m
3000
L
,
m
1000
L 3
A
B
A
B
A 


 and
cm
30
.
0
D
D B
A 
 Eq. (2) gives
73
.
1
1000
3000
L
L
Q
40
.
0
Q
Q
A
B
2
B
A




The flow rate through pipe B s
/
m
23
.
0
73
.
1
40
.
0
Q 3
B 

Worked Example (9)
Water flows through the three pipes shown in the figure. The pipe data
are as follows:
Pipe L ( m ) D ( m ) f
 900 0.30 0.02
 600 0.20 0.018
 1200 0.40 0.017
The gauge pressure at "A" is
2
m
/
kN
550 ; its elevation is
m
5
.
30 and that of "B"
m
3
.
24 . For a total flow of
s
/
m
35
.
0 3
.
The flow rate through pipe B s
/
m
23
.
0
73
.
1
40
.
0
Q 3
B 


Determine the flow through each pipe and the pressure at "B" – Neglect
the minor losses.
Solution
The head loss l
h from A to B is the same no matter which pipe
path
g
2
V
D
l
f
g
2
V
D
l
f
g
2
V
D
l
f
h
2
3
3
3
3
2
2
2
2
2
2
1
1
1
1
l 

 ……….. (1)
The friction head loss in pipe is
g
2
Q
16
D
l
f
g
2
V
D
l
f
h
2
5
2
l 



Substituting in Eq. (a) gives
2
2
3
5
3
3
3
2
2
2
5
2
2
2
2
2
1
1
1
1
l
g
2
Q
16
D
l
f
g
2
Q
16
D
l
f
g
2
Q
16
D
l
f
h









Then
135
.
2
2
.
0
3
.
0
900
600
02
.
0
018
.
0
D
D
l
l
f
f
Q
Q
5
5
2
1
1
2
1
2
2
1

























































….. (2)
Similarly,
135
.
0
4
.
0
3
.
0
900
1200
02
.
0
017
.
0
D
D
l
l
f
f
Q
Q
5
5
3
1
1
3
1
3
3
1

























































…
…….. (3)
The governing equation for parallel pipes is:
3
2
1 Q
Q
Q
Q 

 ……………….. (4)

By combining Eqs. (2), (3) and (4),










519
.
0
1
135
.
2
1
1
Q
/s)
(m
35
.
0
Q 1
3
Thus,
/s
m
199
.
0
Q
,
/s
m
048
.
0
/s, Q
m
103
.
0
Q 3
3
3
2
3
1 


If the only losses included are the main losses, the pressure at point A
can be calculated by apply Bernoulli's equation between point A 1and
point B




A
2
A
A
Z
g
2
V
g
P
B
A
l
B
2
B
B
h
Z
g
2
V
g
P





……………….. (5)
Since the inlet pipe diameter A
D is the same at the exit B
D , B
A V
V 
and equation (5) becomes
 
 
B
A
L
B
A
A
B h
z
z
g
P
P 




 ……………….. (6)
With the total length of the pipe
/s
m
0.103
Q
,
02
.
0
f
,
m
900
l 3
1
1
1 

 and m
30
.
0
D1 , the head loss in
the pipe from A to B
 
 
m
49
.
6
30
.
0
81
.
9
103
.
0
900
02
.
0
8
D
g
Q
l
f
8
h 5
2
2
5
1
2
2
1
1
1
B
A
l 










With m
50
.
30
ZA  , m
30
.
24
ZB  and m
49
.
6
h B
A
l 
 , Eq. (6) gives:

 
  2
B m
/
kN
13
.
546
49
.
6
4
.
24
5
.
30
81
.
9
550
P 




Worked Example (10)
With the valve closed, water flows from tank A to tank B as shown in the
figure. What is the flow rate into tank B when the valve opened to allow
water to flow into tank C also? Neglect all minor losses and assume that
the friction factor is 0.02 for all pipes.
Solution
2
5
2
2
l Q
D
g
l
f
8
g
2
V
D
l
f
h



or
l
h
C
l
h
f
8
D
g
Q l
l
5
2




Diameter of each pipe=0.10
cm
40.0 m
80.0 m
 (0.00)
 (0.00)
 (15.00)
A
B
C
75.0 m

where
l
hl
is the head loss per unit length of a given pipe and C is a
constant=
f
8
D
g 5
2

 . For 02
.
0
f  and m
10
.
0
D  , s
/
m
078
.
0
C 3

(both f and D ) are the same for the given system.
As a first guess, take m
hJ 0
.
5

Pipe from A to J Pipe from J to B Pipe from J to C
m
10
5
15
h J
A
l 


 m
5
0
0
.
5
h B
J
l 


 m
5
0
0
.
5
h C
J
l 



/s
m
0276
.
0
80
10
078
.
0
Q
3
A



s
/
m
0276
.
0
40
5
078
.
0
Q
3
A



s
/
m
020
.
0
75
5
078
.
0
Q
3
C



A
Q is less than  
s
/
m
0476
.
0
020
.
0
0276
.
0
Q
Q 3
C
B 


 .
Since the flow rate towards the junction is less than the sum of the flow
rates out, we guess J
h is high. Reduce m
5
.
2
hJ  and repeat:
m
5
.
12
5
.
2
15
h J
A
l




m
5
.
2
0
5
.
2
h B
J
l




m
5
.
2
0
5
.
2
h C
J
l




/s
m
0308
.
0
80
5
.
12
078
.
0
Q
3
A



s
/
m
0195
.
0
40
5
.
2
078
.
0
Q
3
B



s
/
m
0142
.
0
75
5
.
2
078
.
0
Q
3
C



Still A
Q less than 
s
/
m
0337
.
0
0142
.
0
0195
.
0
Q
Q 3
C
B 


 .
This not closes enough. A better guess would be achieved by reducing
J
h to 2.15m, hence increasing A
Q and reducing both B
Q and C
Q . For
:
m
25
.
2
hJ 

m
85
.
12
15
.
2
15
h J
A
l




m
15
.
2
0
15
.
2
h B
J
l




m
15
.
2
0
15
.
2
h C
J
l




/s
m
0313
.
0
80
85
.
12
078
.
0
Q
3
A



s
/
m
0181
.
0
40
15
.
2
078
.
0
Q
3
B



s
/
m
0132
.
0
75
15
.
2
078
.
0
Q
3
C



A
Q Equals to  
s
/
m
0313
.
0
0132
.
0
0181
.
0
Q
Q 3
C
B 


 .
Worked Example (11)
The three tanks shown in the figure are connected by pipes as indicated.
If minor are neglect, determine the flow rates in each pipe.
This guess gives m
15
.
2
hJ  , which is an acceptable solution.
Hence the discharge from reservoir A towards the junction
  s
/
m
0313
.
0
Q 3
A  is balanced by   s
/
m
0181
.
0
Q 3
B  away
from the junction J to reservoir B and   s
/
m
0132
.
0
Q 3
C 
away from the junction J to reservoir C.

D = 10cm, L =200m and f = 0.015
D = 8cm, L =400m and f = 0.020
D = 8cm, L =200m and f = 0.020
Junction
 A (20.00)
 B (60.00)
 C (0.00)
Elevations are in meters
Solution
The head loss across each pipe in the system is:
2
5
2
2
l Q
D
g
l
f
8
g
2
V
D
L
f
h





 …………………………………………….. (1)
In terms of l
h
,
l
,
D
,
f , Eq. (1) becomes
l
l
5
2
h
C
h
l
f
8
D
g
Q 

 …………………………………………….. (2)
where C is a constant
l
f
8
D
g 5
2


With m
200
l
,
015
.
0
f 
 and m
10
.
0
D  (pipe A),
s
/
m
h
10
352
.
6
C 2
5
l
3


 and Eq. (b) becomes

l
3
h
10
352
.
6
Q 

 ……………………………….. (3)
Similarly,
For pipe (b) l
3
h
10
149
.
3
Q 

 …………….. (4)
For pipe (c) l
3
h
10
226
.
2
Q 

 ……………….. (5)
As a first guess, take J
h elevation equal to the middle reservoir water
surface elevation, .
m
20
hJ  this saves the calculation 0
QB  .
(Assuming 0
P
P
P C
B
A 

 "gauge")
Pipe A Pipe B Pipe C
m
40
20
60
h J
A
l 


 0
h B
J
l 
 m
20
0
20
h C
J
l 



/s
m
040
.
0
40
10
352
.
6
Q
3
3
A



 
0
QB  /s
m
00995
.
0
20
10
226
.
2
Q
3
3
C



 
A
Q  C
Q . This is not the correct solution, we guessed J
h too low.
Increase J
h to 45 and repeat:
m
40
20
60
h J
A
l 


 m
25
20
45
h B
J
l 


 m
45
0
45
h C
J
l 



/s
m
0246
.
0
15
10
352
.
6
Q
3
3
A



 
/s
m
0157
.
0
25
10
149
.
3
Q
3
3
A



 
/s
m
0149
.
0
45
10
226
.
2
Q
3
3
C



 
A
Q ≠  
s
/
m
0306
.
0
0149
.
0
0157
.
0
Q
Q 3
C
B 




This not closes enough. A better guess would be achieved by reducing
J
h to 40.20m, hence increasing A
Q and reducing both B
Q and C
Q .
For :
m
20
.
40
hJ 
m
80
.
19
20
.
40
60
h J
A
l 


 m
20
.
20
20
20
.
40
h B
J
l 


 m
20
.
40
0
20
.
40
h C
J
l 



/s
m
02826
.
0
8
.
19
10
352
.
6
Q
3
3
A



 
/s
m
01415
.
0
20
.
20
10
149
.
3
Q
3
3
A



 
/s
m
01411
.
0
45
10
226
.
2
Q
3
3
C



 
A
Q Equals to  
s
/
m
02826
.
0
01411
.
0
01415
.
0
Q
Q 3
C
B 


 .
Faculty of Engineering Jan. 2012
"Bernoulli's Equation and its Applications – Siphoning Action"
(45)
(75)
(64.5)



L = 1200m, D = 200mm,
f = 0.018
L =1800m, D = 200mm,
f = 0.018
 Calculate: The flow rate and the gage
reading, neglecting local
losses and velocity heads.
Solution

 To determine the velocity V, first apply the steady flow energy
between point "A" on the free surface of upper reservoir and point "B"
on the lower reservoir respectively,
 























 B
A
L
A
2
A
2
h
g
2
V
g
P
Z
g
2
V
g
P
Z ………………….. (1)
The loss due to friction in the pipes "1" and "2" is given by the Darcy's as
g
2
V
D
L
f
g
2
V
D
L
f
h
2
2
2
2
2
2
1
1
1
1
B
A
L 





At both points A and B the pressure is atmospheric, so that
0
)
gage
(
p
p
p B
A 


Also, if the area of the free surface of both reservoirs is large, the
velocity at A and B is negligible. Thus
g
2
V
D
L
f
g
2
V
D
L
f
Z
Z
2
2
2
2
2
2
1
1
1
1
B
A 

 ………………….. (2)
 hL =75 - 45
= 30 m
(45)
(75)
(64.5)



L1 = 1200m, D1 = 200mm,
f1 = 0.018
L2 =1800m, D2 = 200mm,
f2 = 0.018
A
B
E G L
C
g
2
V
D
L
f
g
2
V
D
L
f
Z
Z
2
2
2
2
2
2
1
1
1
1
B
A 



Putting ZA – ZB = 75 – 45 = 30m, f1 = f2 = f = 0.018, D1 = D2 = D = 0.20
m, V1 = V2 = Vp, L1 = 1200 m, L2 =1800 m
 
1800
1200
2
.
0
81
.
9
2
V
018
.
0
30
2
p





Solving for Vp gives
mls
48
.
1
3000
018
.
0
2
.
0
81
.
9
2
30
Vp 





The flow rate s
/
L
46
s
/
m
046
.
0
48
.
1
4
2
.
0
V
A
Q 3
2
p 









 



 
 To find the gage pressure pC at C, apply the steady energy equation
between "A" and "C"
 























 C
A
L
c
2
A
2
h
g
2
V
g
P
Z
g
2
V
g
P
Z ………….. (3)
Since pA = 0, ZA = 75 m, ZB = 64.5 m, and VC = Vp
 
g
2
V
D
L
f
g
2
V
g
P
5
.
64
0
0
75
2
p
1
c
2
p
C
A 















or
  










 D
L
f
1
g
2
V
5
.
64
75
g
P 1
2
p
C
…………………..(4)
For f = 0.018, L1 = 1200 m, and Vp = 1.48 m, Eq. (4) gives

  water
of
m
67
.
1
2
.
0
1200
018
.
0
1
81
.
9
2
48
.
1
5
.
64
75
g
P 2
C







 








The gage reading is 1.67m of water (vacuum)

Worked Example (12)
The three water-filled tanks shown in the figure are connected by pipes
as indicated. If minor losses are neglected, determine the flow rate in
each pipe.
D = 0.08m &
L = 200m& f =0.020
D = 0.10m &
L = 200m& f =0.015
D = 0.08m &
L = 400m& f = 0.020
 (20.0)
 (60.0)
 (00.0)

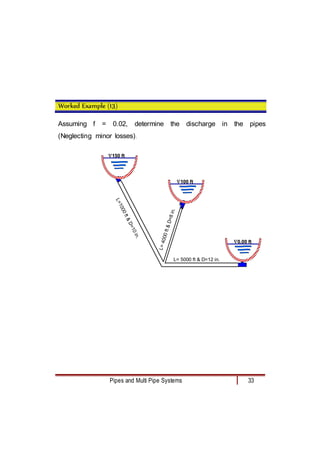
Worked Example (13)
Assuming f = 0.02, determine the discharge in the pipes
(Neglecting minor losses).
150 ft
100 ft
0.00 ft
L
=
1
0
0
0
f
t
&
D
=
1
0
i
n
.
L
=
4
0
0
0
f
t
&
D
=
8
i
n
.
L= 5000 ft & D=12 in.

Practical Problems
What power must the pump supply to the system to pump the oil
from the lower reservoir to the upper reservoir at a rate of
s
/
m
20
.
0 3
? Sketch the HGL and the EGL for the system.
If the water surface elevation in reservoir B is m
110 , what must be
the water surface elevation in reservoir A if a flow s
/
m
03
.
0 3
is to
occur in the cast-iron pipe?. Draw the HGL and the EGL, including
relative slopes and changes in slope.
Two pipes are connected in parallel. One pipe is twice the
diameter of the other and three times as long. Assume that f in the
large pipe is 0.02 and f in the smaller one is 0.013. Determine the
ratio of the discharge in the two pipes.

Solved problems pipe flow final 1.doc

More Related Content

What's hot (20)

Similar to Solved problems pipe flow final 1.doc (20)

More from Dr. Ezzat Elsayed Gomaa (20)

Recently uploaded (20)

Solved problems pipe flow final 1.doc