Sorting in data structures and algorithms , it has all the necessary points to consider
- 2. ● Different sorting algorithms: ○ Bubble Sort ○ Selection Sort ○ Insertion Sort ○ Merge Sort ○ Quick Sort ○ Heap Sort Sorting Algorithms 2
- 3. Bubble Sort Successively bubbles up largest elements one by one, to the end of the array Sorts the array in “at most” n-1 passes How to find complexity? (Worst case) Bubble Sort
- 4. Selection Sort Selects minimum element from the remaining array and places it in the beginning of the array Sorts the array in “at most” n-1 passes How to find complexity? (Worst case) Selection Sort
- 5. Inserts every element at its right place in a sorted array. Sorts the array in n-1 passes How to find complexity? (Worst case) Insertion Sort Insertion Sort
- 6. Merge Sort Merge Sort Sorts an array by dividing it into two halves RECURSIVELY and then merging the sorted array back into a sorted array. If T(N) = time to sort array of size “N” T(N) = 2xT(N/2) + cN Merging Takes time proportional to “N”
- 7. Merge Sort T(N) = 2.T(N/2) + cN T(N) = 2.[2T(N/4)+cN/2] + cN = 4.T(N/4) + 2.cN/2 + cN = 4.T(N/4) + 2.cN = 22.T(N/22) + 2.cN Now, 4.T(N/4) + 2.cN can be further solved to obtain = 8.T(N/8) + 3.cN = 23.T(N/23) + 3.cN Say T(N) = 2k.T(N/2k) + k.cN (if mergeSort goes for k recursions)
- 8. Merge Sort Say T(N) = 2k.T(N/2k) + k.cN (if mergeSort goes for k recursions) Now T(1) = constant, say d So Recursions will stop When N/2k = 1 Or N = 2k Or k = log2 N T(N) = N.T(1) + (log2 N)cN T(N) = O(N) + O(Nlog2 N) T(N) = O(Nlog2 N)
- 9. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 10. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 11. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 12. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 13. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 14. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 15. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 16. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 17. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 18. -1 4 7 2 1 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 19. -1 1 2 7 4 5 3 0 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 20. -1 1 2 7 4 5 3 0 9 3 4 5 0 1 2 6 7 8 Now do the breaking and merging on this side Merge Sort
- 21. -1 1 2 7 4 0 3 5 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 22. -1 0 1 3 2 4 5 7 9 3 4 5 0 1 2 6 7 8 Merge Sort
- 23. -1 2 4 0 7 1 3 5 9 3 4 5 0 1 2 6 7 8 -1 0 1 3 2 4 5 7 9 k j i Merging the arrays (in sorted orders)
- 24. -1 0 2 7 4 1 3 5 9 3 4 5 0 1 2 6 7 8 i j mid IN-PLACE = Without using a third array (and only working on indices at different positions in the array) Merging the arrays (in sorted orders)
- 25. -1 0 2 7 4 1 3 5 9 3 4 5 0 1 2 6 7 8 i j mid First half Second half Merging the arrays (in sorted orders)
- 26. -1 0 2 7 4 1 3 5 9 3 4 5 0 1 2 6 7 8 i j mid -1 < 1 ⇒ i++ Merging the arrays (in sorted orders)
- 27. -1 0 2 7 4 1 3 5 9 3 4 5 0 1 2 6 7 8 i j mid 0 < 1 ⇒ i++ Result array Note how first sub-array shrinks when something from first sub-array contributes to the building of resultant array WHATEVER is BEHIND (to the left of) “i” becomes the result array Merging the arrays (in sorted orders)
- 28. -1 0 2 7 4 1 3 5 9 3 4 5 0 1 2 6 7 8 i j mid Merging the arrays (in sorted orders)
- 29. -1 0 2 7 4 1 3 5 9 3 4 5 0 1 2 6 7 8 i j mid 2 > 1 - Temp = 1 2,1 caused an inversion Merging the arrays (in sorted orders)
- 30. -1 0 2 7 4 1 3 5 9 3 4 5 0 1 2 6 7 8 i j mid 2 > 1 - Temp = 1 (2,1) caused an inversion All elements to the right of 2 in first sub-array are greater than 2 So elements from i to mid are going to cause inversion with 1 as well… So there will be total of mid-i (number of elements from i to mid) inversions Merging the arrays (in sorted orders)
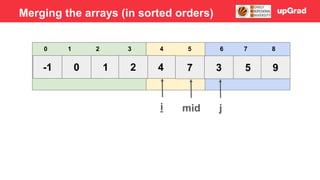
- 31. -1 0 2 4 2 7 3 5 9 3 4 5 0 1 2 6 7 8 i j mid 2 > 1 - Temp = 1 - Shift 7, 4, 2 to the right Merging the arrays (in sorted orders)
- 32. -1 0 1 4 2 7 3 5 9 3 4 5 0 1 2 6 7 8 i j mid 2 > 1 - Temp = 1 - Shift 7, 4, 2 to the right - Arr[i] = temp Merging the arrays (in sorted orders)
- 33. -1 0 1 4 2 7 3 5 9 3 4 5 0 1 2 6 7 8 i j mid 2 > 1 - I++ - Mid++ (something from second half was added to result. . so an element of second half is deleted and moved and the boundary of first half is shifted right) - J++ Merging the arrays (in sorted orders)
- 34. -1 0 1 4 2 7 3 5 9 3 4 5 0 1 2 6 7 8 i j mid Note how second sub-array shrinks and first sub-array moves to the right when something from second sub array contributes towards building the resulting sub-array Merging the arrays (in sorted orders)
- 35. -1 0 1 4 2 7 3 5 9 3 4 5 0 1 2 6 7 8 i j mid 2 < 3 ⇒ i++ Merging the arrays (in sorted orders)
- 36. -1 0 1 4 2 7 3 5 9 3 4 5 0 1 2 6 7 8 i j mid Merging the arrays (in sorted orders)
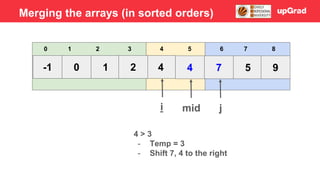
- 37. -1 0 1 4 2 7 3 5 9 3 4 5 0 1 2 6 7 8 i j mid 4 > 3 - Temp = 3 Merging the arrays (in sorted orders)
- 38. -1 0 1 4 2 4 7 5 9 3 4 5 0 1 2 6 7 8 i j mid 4 > 3 - Temp = 3 - Shift 7, 4 to the right Merging the arrays (in sorted orders)
- 39. -1 0 1 3 2 4 7 5 9 3 4 5 0 1 2 6 7 8 i j mid 4 > 3 - Temp = 3 - Shift 7, 4 to the right - Arr[i] = temp Merging the arrays (in sorted orders)
- 40. -1 0 1 3 2 4 7 5 9 3 4 5 0 1 2 6 7 8 i j mid 4 > 3 - i++ - mid++ - j++ Merging the arrays (in sorted orders)
- 41. -1 0 1 3 2 4 7 5 9 3 4 5 0 1 2 6 7 8 i j mid 4 > 3 - i++ - mid++ - j++ Merging the arrays (in sorted orders)
- 42. -1 0 1 3 2 4 7 5 9 3 4 5 0 1 2 6 7 8 i j mid 4 < 5 - i++ Merging the arrays (in sorted orders)
- 43. -1 0 1 3 2 4 7 5 9 3 4 5 0 1 2 6 7 8 i j mid Merging the arrays (in sorted orders)
- 44. -1 0 1 3 2 4 7 5 9 3 4 5 0 1 2 6 7 8 i j mid 7>5 - Temp = 5 Merging the arrays (in sorted orders)
- 45. -1 0 1 3 2 4 7 7 9 3 4 5 0 1 2 6 7 8 i j mid 7>5 - Temp = 5 - Shift 7 to right Merging the arrays (in sorted orders)
- 46. -1 0 1 3 2 4 5 7 9 3 4 5 0 1 2 6 7 8 i j mid 7>5 - Temp = 5 - Shift 7 to right - Arr[i] = temp Merging the arrays (in sorted orders)
- 47. -1 0 1 3 2 4 5 7 9 3 4 5 0 1 2 6 7 8 i j mid 7>5 - I++ - Mid++ - J++ Merging the arrays (in sorted orders)
- 48. -1 0 1 3 2 4 5 7 9 3 4 5 0 1 2 6 7 8 i j mid i<=mid Merging the arrays (in sorted orders)
- 49. -1 0 1 3 2 4 5 7 9 3 4 5 0 1 2 6 7 8 i j mid 7 < 9 ⇒ i++ and i becomes greater than mid Merging the arrays (in sorted orders)
- 50. -1 0 1 3 2 4 5 7 9 3 4 5 0 1 2 6 7 8 Array Sorted ! Merging the arrays (in sorted orders)
- 51. Quick Sort ● Quick Sort ○ Select a pivot ■ First element ■ Last element ■ Any random element ■ Select middle element as the pivot ○ Place pivot at its proper place in the array ■ Elements less than pivot are on one side ■ Elements greater than pivot are on the other side of pivot ○ Perform quickSort on the two halves
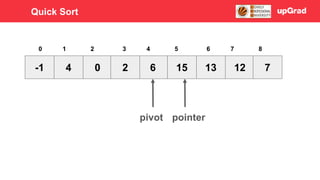
- 52. -1 4 7 12 2 15 13 0 6 3 4 5 0 1 2 6 7 8 pivot pointer Quick Sort
- 53. -1 4 7 12 2 15 13 0 6 3 4 5 0 1 2 6 7 8 pivot pointer Quick Sort
- 54. -1 4 7 12 2 15 13 0 6 3 4 5 0 1 2 6 7 8 pivot pointer Quick Sort
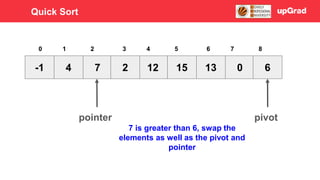
- 55. -1 4 7 12 2 15 13 0 6 3 4 5 0 1 2 6 7 8 pivot pointer 7 is greater than 6, swap the elements as well as the pivot and pointer Quick Sort
- 56. -1 4 6 12 2 15 13 0 7 3 4 5 0 1 2 6 7 8 pointer pivot Quick Sort
- 57. -1 4 6 12 2 15 13 0 7 3 4 5 0 1 2 6 7 8 pointer pivot Quick Sort
- 58. -1 4 6 12 2 15 13 0 7 3 4 5 0 1 2 6 7 8 pointer pivot 0 is less than 6 => Swap the elements as well as the pivot and pointer Quick Sort
- 59. -1 4 0 12 2 15 13 6 7 3 4 5 0 1 2 6 7 8 pivot pointer Quick Sort
- 60. -1 4 0 12 2 15 13 6 7 3 4 5 0 1 2 6 7 8 pivot pointer Quick Sort
- 61. -1 4 0 12 2 15 13 6 7 3 4 5 0 1 2 6 7 8 pivot pointer Quick Sort
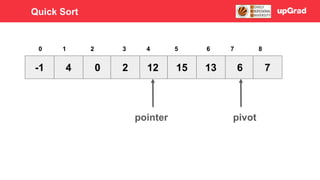
- 62. -1 4 0 6 2 15 13 12 7 3 4 5 0 1 2 6 7 8 pointer pivot Quick Sort
- 63. -1 4 0 6 2 15 13 12 7 3 4 5 0 1 2 6 7 8 pointer pivot Quick Sort
- 64. -1 4 0 6 2 15 13 12 7 3 4 5 0 1 2 6 7 8 pointer pivot Quick Sort
- 65. -1 4 0 6 2 15 13 12 7 3 4 5 0 1 2 6 7 8 pointer pivot Quick Sort
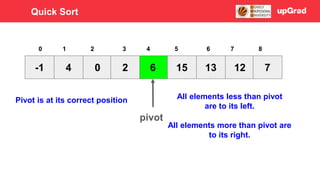
- 66. -1 4 0 6 2 15 13 12 7 3 4 5 0 1 2 6 7 8 pivot Pivot is at its correct position All elements less than pivot are to its left. All elements more than pivot are to its right. Quick Sort
- 67. -1 4 0 6 2 15 13 12 7 3 4 5 0 1 2 6 7 8 Do the same thing here Do the same thing here THEN Quick Sort
- 68. Quick Sort
- 69. Heap Sort
- 70. 1 9 7 4 0 5 3 2 -1 In-place sort = sorting the arrray without using extra space (like an extra array) . . .or sorting that uses O(1) space apart from O(n) which is used store the array which is to be sort Stable sort = If unsorted array has two equal entries A and B (such that A occurs before B, then A will occur before B in the sorted array also. . . such a sorting is called Stable Sort. . . Heap Sort
- 71. 1 9 7 4 0 5 3 2 -1 Calculate N = 9 (Length of the current heap) (Light yellow box) Heap Sort
- 72. 1 9 7 4 0 5 3 2 -1 maxHeapify Method: maxHeapify(arr, N, currentIndex) Arr = the array containing elements [Root is at 0] N = the length of current heap currentIndex = where maxHeapification starts Heap Sort
- 73. 1 9 7 4 0 5 3 2 -1 Now start from parent of last node = (N/2-1) and move up to the root WHILE maxHeapifying the tree at every node. . . N = 9 N/2-1 = 3 Call maxHeapify() as follows maxHeapify(arr,N ,3) maxHeapify(arr,N,2) maxHeapify(arr,N,1) maxHeapify(arr,N,0) 3 4 5 0 1 2 6 7 8 Heap Sort
- 74. 1 9 7 4 0 5 3 2 -1 3 4 5 0 1 2 6 7 8 maxHeapify(arr, N=9, currentIndex = 3) Assume the currentIndex to be the index of Largest element indexOfLargest Heap Sort
- 75. 1 9 7 4 0 5 3 2 -1 3 4 5 0 1 2 6 7 8 Find the INDICES OF left and right children of currentIndex leftChildIndex = 2*currentIndex +1 rightChildIndex = 2*currentIndex +2 indexOfLargest Note that root is at 0 And not 1 leftChildIndex rightChildIndex maxHeapify(arr, N=9, currentIndex = 3) Heap Sort
- 76. 1 9 7 4 0 5 3 2 -1 3 4 5 0 1 2 6 7 8 If the index of left child is not out of the current heap (less than N) And element at leftChildIndex is more than element at indexOfLargest Then leftChildIndex becomes indexOfLargest indexOfLargest Note that root is at 0 And not 1 leftChildIndex rightChildIndex maxHeapify(arr, N=9, currentIndex = 3) Heap Sort
- 77. 1 9 7 4 0 5 3 2 -1 3 4 5 0 1 2 6 7 8 If the index of left child is not out of the current heap (less than N) And element at leftChildIndex is more than element at indexOfLargest Then leftChildIndex becomes indexOfLargest currentIndex Note that root is at 0 And not 1 leftChildIndex rightChildIndex indexOfLargest maxHeapify(arr, N=9, currentIndex = 3) Heap Sort
- 78. 1 9 7 4 0 5 3 2 -1 3 4 5 0 1 2 6 7 8 If the index of right child is not out of the current heap (less than N) And element at rightChildIndex is more than element at indexOfLargest Then rightChildIndex becomes indexOfLargest Which is not the case here currentIndex Note that root is at 0 And not 1 leftChildIndex rightChildIndex indexOfLargest maxHeapify(arr, N=9, currentIndex = 3) Heap Sort
- 79. 1 9 7 4 0 5 3 2 -1 3 4 5 0 1 2 6 7 8 If indexOfLargest is not CurrentIndex Then swap currentIndex element with the index of largest element currentIndex Note that root is at 0 And not 1 leftChildIndex rightChildIndex indexOfLargest maxHeapify(arr, N=9, currentIndex = 3) Heap Sort
- 80. 1 9 7 4 2 5 3 0 -1 3 4 5 0 1 2 6 7 8 If indexOfLargest is not CurrentIndex Then swap currentIndex element with the index of largest element currentIndex Note that root is at 0 And not 1 leftChildIndex rightChildIndex indexOfLargest maxHeapify(arr, N=9, currentIndex = 3) Heap Sort
- 81. 1 9 7 4 2 5 3 0 -1 3 4 5 0 1 2 6 7 8 We have sent zero down the heap. . which may violate heap property with its own children. . [Note: IndexOfLargest will be at a position from where the largest element was picked for swapping,i.e, Left child or right child. If the swapping happened at all] Therefore, call maxHeapify(arr, N=9, currentIndex = indexOfLargest) currentIndex leftChildIndex rightChildIndex indexOfLargest maxHeapify(arr, N=9, currentIndex = 3) Heap Sort
- 82. 1 9 7 4 2 5 3 0 -1 3 4 5 0 1 2 6 7 8 We have sent zero down the heap. . which may violate heap property with its own children. . Also note that if swapping happened, then indexOfLargest will not be at currentIndex, it will be either at left child or at right child of the current index (or indexOfLargest will be down the tree) currentIndex leftChildIndex rightChildIndex indexOfLargest maxHeapify(arr, N=9, currentIndex = 3) Heap Sort
- 83. Array Has been heapified 9 4 7 1 2 5 3 0 -1 3 4 5 0 1 2 6 7 8 Heap Sort
- 84. Now sorting the array 9 4 7 1 2 5 3 0 -1 3 4 5 0 1 2 6 7 8 Swap the first node with the last node Assume last node to be out of the heap . . so size of heap is N-1 (or 9-1 = 8) Heap Sort
- 85. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Swap the first node with the last node Assume last node to be out of the heap . . so size of heap is N-1 (or 9-1 = 8) Now sorting the array Heap Sort
- 86. -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Do maxHeapify on array taking heap size as 8 and starting from 0 Basically we are going to heapifyDown from the root node Now sorting the array Heap Sort
- 87. maxHeapify(arr, N=8, currentIndex = 0) -1 4 7 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Current largest index = index 0 Find largest. . .which will be index 2. . . Swap 7 with -1 Heap Sort
- 88. 7 4 -1 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Now call maxHeapify on Index 2 (or the index with which the swap happened) maxHeapify(arr, N=8, currentIndex = 0) Heap Sort
- 89. 7 4 -1 1 2 5 3 0 9 3 4 5 0 1 2 6 7 8 Assume largest to be at index 2. . . Children of index 2 are at index 5 and index 6 Largest will be at index 5 . so we swap -1 with 5. maxHeapify(arr, N=8, currentIndex = 0) Heap Sort
- 90. 7 4 -1 1 5 -1 3 0 9 3 4 5 0 1 2 6 7 8 Assume largest to be at index 2. . . Children of index 2 are at index 5 and index 6 Largest will be at index 5 . so we swap -1 with 5. maxHeapify(arr, N=8, currentIndex = 0) Heap Sort
- 91. 7 4 -1 1 5 -1 3 0 9 3 4 5 0 1 2 6 7 8 Now do the mixheapify on index 5 Left child index of index 5 is 11 [outside the range of current heap] Right child is also outside the range of current Heap (that is 8) Therefore no more swapping is involved maxHeapify(arr, N=8, currentIndex = 0) Heap Sort
- 92. 7 4 -1 1 5 -1 3 0 9 3 4 5 0 1 2 6 7 8 After the remaining array has been max heapified. . . Swap first node with the last node maxHeapify(arr, N=8, currentIndex = 0) Heap Sort
- 93. 7 4 -1 1 5 -1 3 0 9 3 4 5 0 1 2 6 7 8 After the remaining array has been max heapified. . .i value will again decrease and the length of heap will decrease by 1) maxHeapify(arr, N=8, currentIndex = 0) Heap Sort
- 94. 0 4 -1 1 5 -1 3 7 9 3 4 5 0 1 2 6 7 8 Swap last node with the first node Again do the max heapify on the array of size 7 maxHeapify(arr, N=8, currentIndex = 0) Heap Sort






![Merge Sort
T(N) = 2.T(N/2) + cN
T(N) = 2.[2T(N/4)+cN/2] + cN
= 4.T(N/4) + 2.cN/2
+ cN
= 4.T(N/4) + 2.cN
= 22.T(N/22) + 2.cN
Now, 4.T(N/4) + 2.cN can be
further solved to obtain
= 8.T(N/8) + 3.cN
= 23.T(N/23) + 3.cN
Say T(N) = 2k.T(N/2k) + k.cN
(if mergeSort goes for k
recursions)](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/85/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-7-320.jpg)
























![-1 0 1 4
2 7 3 5 9
3 4 5
0 1 2 6 7 8
i j
mid
2 > 1
- Temp = 1
- Shift 7, 4, 2 to the
right
- Arr[i] = temp
Merging the arrays (in sorted orders)](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/85/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-32-320.jpg)




![-1 0 1 3
2 4 7 5 9
3 4 5
0 1 2 6 7 8
i j
mid
4 > 3
- Temp = 3
- Shift 7, 4 to the right
- Arr[i] = temp
Merging the arrays (in sorted orders)](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/85/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-39-320.jpg)






![-1 0 1 3
2 4 5 7 9
3 4 5
0 1 2 6 7 8
i
j
mid
7>5
- Temp = 5
- Shift 7 to right
- Arr[i] = temp
Merging the arrays (in sorted orders)](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/85/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-46-320.jpg)





















![1 9 7 4
0 5 3 2 -1
maxHeapify Method: maxHeapify(arr, N, currentIndex)
Arr = the array containing elements [Root is at 0]
N = the length of current heap
currentIndex = where maxHeapification starts
Heap Sort](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/85/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-72-320.jpg)








![1 9 7 4
2 5 3 0 -1
3 4 5
0 1 2 6 7 8
We have sent zero down the heap. . which may violate heap property with its own
children. .
[Note: IndexOfLargest will be at a position from where the largest element was
picked for swapping,i.e, Left child or right child. If the swapping happened at all]
Therefore, call maxHeapify(arr, N=9, currentIndex = indexOfLargest)
currentIndex
leftChildIndex rightChildIndex
indexOfLargest
maxHeapify(arr, N=9, currentIndex = 3)
Heap Sort](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/85/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-81-320.jpg)









![7 4 -1 1
5 -1 3 0 9
3 4 5
0 1 2 6 7 8
Now do the mixheapify on index 5
Left child index of index 5 is 11 [outside the range of current heap]
Right child is also outside the range of current Heap (that is 8)
Therefore no more swapping is involved
maxHeapify(arr, N=8, currentIndex = 0)
Heap Sort](https://image.slidesharecdn.com/sorting-240129142601-5dcfb2ea/85/Sorting-in-data-structures-and-algorithms-it-has-all-the-necessary-points-to-consider-91-320.jpg)




