Supervised learning for IOT IN Vellore Institute of Technology
- 2. Supervised Learning • Two types of data samples • Training: Used to extract features and train the machine learning algorithm • Testing: Used to predict the label for the given test data • Supervised learning can be used for both classification and regression tasks
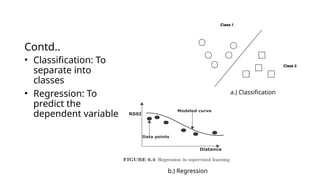
- 3. Contd.. • Classification: To separate into classes • Regression: To predict the dependent variable a.) Classification b.) Regression
- 4. k- Nearest Neighbors • Based on majority voting among nearest neighbors, the sample is classified into the majority class. • Consider the example on the right • Classify the point <Temperature = 4 and Humidity = 8> with = 3. Temperature Humidity Class a 8 8 Warm b 8 5 Warm c 4 5 Cool d 2 5 Cool e 9 9 Warm
- 5. Contd.. • Denote the test sample as x. • Using Euclidean measure: • D(x, a) = • D(x, b) = • D(x, c) = • D(x, d) = • D(x, e) = • Clearly c, d and a are the nearest neighbors of x. Majority of the nearest neighbors (2 out of 3) fall in the Cool class. Therefore, x is Cool.
- 6. Naïve Bayes Classification • Conditional probability
- 7. Contd.. • Consider the example given. • P(Sunny) = 3/12 • P(Rainy) = 4/12 • P(Windy) = 5/12 • P (No) = 3/12 • P(Yes) = 9/12 • Find P(Yes|Windy) • P (Windy|Yes) = 3/9 (In 9 Yes, there are 3 Windy) • Weather No Yes Probability Sunny 1 2 Rainy 0 4 Windy 2 3 Probabilit y
- 8. Linear Regression • The equation of a line • y = ax + b • Calculate b as • Calculate a as = days 1 2 4 6 7 = productivity 2 3 5 4 10
- 9. Linear Regression • = 0.8 • If x = 8, y = 8.8. = days 1 2 4 6 7 = productivity 2 3 5 4 10
- 10. Limitations of Linear Regression • Linear regression gives a numerical result • Logistic regression gives an output between 0 and 1 • If the output is greater than some threshold, say, 0.5, the logistic regression gives 1, otherwise 0
- 11. Logistic Regression • Define z • Logistic regression defines probability as:
- 12. Contd.. • Assume that the hypothesis for linear regression is • Ques. 1. Determine the probability of having a disease who has glucose level 30. • Glucose level Result 18 0 16 0 32 1 27 1 40 1
- 13. Contd.. • Assume that the hypothesis for linear regression is • Ques. 2. What glucose level ensures a probability of more than 98%? • • = 0.020408 • z = 3.891828 • Putting z in • Glucose Level = 29.945914. Glucose level Result 18 0 16 0 32 1 27 1 40 1
- 14. Unsupervised Learning • In unsupervised learning, given data samples, we group similar data together • Data samples are clustered based on similarity Flowchart of Unsupervised Learning Clustering
- 15. Principal Component Analysis • Unsupervised learning technique for dimensionality reduction in N-dimensional datasets • Reduced dimensionality eliminates redundancy • Keep maximum variance among reduced axis • Before applying PCA, we make the data set having zero mean using the centering technique
- 16. Contd.. • Find the first principal component of the data in Table 6.5 • Note that • • Table 6.6 gives important parameters 2.4375 = Soil Moisture 2 1 0 -1 = Leaf Wetness 4 3 1 0.5 Smart agriculture data for PCA problem
- 17. Contd.. • (By taking values from Table 6.6) • Similarly, • Similarly
- 18. Contd.. • S = = • Put • = 0 • Solving this equation (using calculator or online tool), you will get roots as 4.35 and 0.052. 1.67 2.08 2.08 2.73
- 19. Contd.. • Considering the largest eigenvalue, we get the first principal component from the eigen-vector direction. • Get eigenvector as: • Solve •
- 20. Contd.. • • Now, 2D data is reduced to 1D data in the direction of the principal component. • Therefore, transforming the data into new subspace as:
- 21. Bias and Variance Tradeoff • Underfitting • The data is modelled by an order lower than the actual order of the model. • High bias condition • Overfitting • The data is modelled by an order higher than the actual order of the model. • High variance condition • The model memorizes the training data • If we apply unseen test data to this overfitted model, the error is high.
- 22. Contd.. • The data on the right shows a quadratic model • If we plot the data using these three plots: • The RMSE is 1.724, 0.3696, 0.3227 for the first, second, and the third order models respectively • Even though the RMSE is least for the third order model, it is an overfitted model. Data and its scatter plot! 0 1 2 3 4 0 1 4.8 9.4 15.5
- 23. Artificial Neural Networks • Take inspiration from neurons in human brain • Dendrites are the thin fiber that carries information from other neurons. • The information transmitted between the dendrites and axons is carried out by the synapse • This information is then passed to the cell body for processing. • Axon carries impulses from the cell body to other cells. • Dendrites, synapse, cell body (or soma), and axon of a biological neuron correspond to input, weight, node, and output of an artificial neuron, respectively • We get the output if the sum of weighted information is greater than a threshold.
- 24. Perceptron Model • A single unit of neuron • The output is unity if the weighted sum of the input is greater than zero. • For example: • If , , , , , and , the weighted sum of inputs is 7 and hence the output is 1. On the other hand, if , , , , , and , the weighted sum of inputs is -1 and hence the output is 0.
- 25. Activation Function • Activation function decides whether a neuron will be activated or not • Activation function helps us to introduce non-linearity which is helpful in learning complex models • There are many different activation functions discussed in literature
- 26. Linear and Binary Step Activation Functions h(𝑥)=𝑥
- 27. Sigmoid and Tanh Activation Functions h(𝑥)= 1 1+𝑒 −𝑥 h(𝑥)= 𝑒𝑥 −𝑒−𝑥 𝑒 𝑥 +𝑒 −𝑥 Tanh activation function is also known as Bipolar Sigmoid activation function
- 28. ReLU Activation Function • Most used. • Efficient
- 29. Loss Functions • The objective in training neural networks is to minimize the loss function. Different loss functions are: • Mean Absolute Error (MAE) • Here, is the predicted value and is the true value • Mean Squared Error (MSE) • Cross-Entropy (CE) Loss • Used in Classification problems • Here p is the true distribution, and q is the estimated distribution • Here, is the Kullback-Leibler divergence between the two distributions
- 30. Back-propagation • Backpropagation is used to train neural networks • Compute the gradient of a cost function with respect to all the weights in the network and backpropagate error (loss) information • Consider the example:
- 31. Contd… • Solution • Similarly, • Subsequently, the loss is computed using the mean squared error as • [desired is assumed to be 1]
- 32. Contd… • Solution • This error must be backpropagated through the neural network • First, we calculate • Denote, , then • So, • Then, • And
- 33. Contd… • Solution • Denote • Also, • Using chain rule for derivatives, we have: • Assume the learning rate • Update • Similarly, calculate for
- 34. Optimization in Back-Propagation • Gradient Descent Method • First derivative of a scalar function E(w) with respect to a vector w = [w1, w2]T is called the gradient of E(w) or • The second derivative of a scalar function E(w) with respect to a vector is a matrix called the Hessian of or
- 35. Contd… • Batch gradient descent • Computes the gradient of the cost function with respect to the parameters w for the entire training dataset • For a function , derivative (slope at point w) of it is • A small change () in the input can cause the output to move to a value given by [via first order Taylor series] • Assuming minimization, we take a jump such that y reduces • Gradient descent proposes weight update as • Here is the learning rate and m is the batch-size
- 36. Contd… • Batch Gradient Descent (Example): • Let there be 100 samples in a dataset that are used for training the model • For batch gradient descent, batch size = 100 and there is only 1 batch • The updated weight w’ is obtained by summing the gradients of all losses considering all samples and then averaging them • Here,
- 37. Contd… • Batch Gradient Descent (Example): • If there are 6 examples in the dataset, • Let the target values corresponding to examples be respectively • Let the weights associated with these examples are • Let the derivative of loss for be 0.5, 0.2, 0.7, 0.4, 0.7, and 0.6 respectively initially. • Using gradient descent, we update weight as follows: • Since, and let • Similarly, all weights are updated until convergence or maximum number of allowed iterations
- 38. Contd… • Minibatch gradient descent • Perform update for every mini-batch of n examples. • The weight is updated as: • Here, is the learning rate and . Mini-batch size is a hyperparameter
- 39. Contd… • Mini-batch gradient descent (Example): • Let there be 100 samples • Mini-batches = 5, Batch-size = 20 • Updated weight w’ is obtained by summing the gradients of losses considering 20 samples and then averaging them • Here, • Update weight for each mini-batch till convergence or maximum number of allowed iterations
- 40. Contd… • Mini-batch gradient descent (Example): • Consider the same example as Batch Gradient Descent • Consider 2 mini-batches with batch-size of 3 • Using minibatch gradient descent, is updates as: • • Similarly, all weights are updated until convergence or maximum number of allowed iterations
- 41. Contd… • Stochastic Gradient Descent • In stochastic gradient descent, a single parameter update takes place • It is fast as it avoids redundancy that exists in batch gradient descent • It performs frequent updates with a high variance that causes the objective function to fluctuate heavily
- 42. Contd… • Stochastic gradient descent (Example): • Consider 100 samples in a dataset • Batch size = 1, Number of batches = 100 • Updated weight w’ is obtained by summing the gradients of loss of each sample at a time • Here, • The weight is updated for every single sample • The oscillation is very high compared to gradient descent before reaching global optima
- 43. Contd… • Stochastic gradient descent (Example): • Consider the same example as Batch Gradient Descent • Using SGD, we update weight as follows • Here, , • SGD is faster when compared with GD • However, weight update oscillates with SGD • GD updates convergence without much oscillations
- 44. Evaluation Methods • Dataset is divided into train and test sets • Train set • Used for model training • Test set • Disjoint from training set • Also called holdout set • Validation set (sometimes a 3-way split) • Sometimes test set is held out to give only the final answer • In that case, validation set can be used as an intermediary test set • An example of overfitting is when the training loss decreases but the validation loss increases
- 45. Contd.. • n-fold Cross-validation • If we are running the algorithm for n times, and using the same test data, chances are that overfitting will occur • Instead, we divide the dataset into n parts. We use each part as a test set in different iteration and the remaining (n-1) parts combined as the training set • In this way, we have a new test set every iteration, and the dataset size is the same • The procedure runs n times and gives n accuracies. The final accuracy is the average of the n accuracies • Leave-one-out Cross-validation • This method is used when the dataset is very small • Each fold of the cross-validation has only a single test example. The rest of the data is used for training • If the original data has m-examples, we can run the procedure over m-iterations and get the average
- 46. Performance Metrics • Accuracy • Ratio of the number of correctly predicted results to the total number of predicted results • Precision • Number of correctly classified positive examples divided by the total number of examples that are classified as positive • Recall • Number of correctly classified positive examples divided by the total number of actual positive examples in the test set • F1 Score • Combination of precision and recall into one measure • • If FP = FN = 0, then F1 Score = 1 Confusion Matrix
- 47. Contd.. • If TP = 1, TN = 1000, FP = 0, and FN = 99, then from equations before, we get: accuracy = 91 %, precision p = 100%, recall r =1%. • F1 Score = • Note • F1-score is a harmonic mean • F1-score tends to be closer to the smaller of the two: precision and recall • Useful to determine the worst performance of the two





























![Contd…
• Solution
• Similarly,
• Subsequently, the loss is computed using the mean squared error
as
• [desired is assumed to be 1]](https://image.slidesharecdn.com/supervisedlearning-241026091801-db6d9762/85/Supervised-learning-for-IOT-IN-Vellore-Institute-of-Technology-31-320.jpg)


![Optimization in Back-Propagation
• Gradient Descent Method
• First derivative of a scalar function E(w) with respect to a vector w =
[w1, w2]T
is called the gradient of E(w) or
• The second derivative of a scalar function E(w) with respect to a
vector is a matrix called the Hessian of or](https://image.slidesharecdn.com/supervisedlearning-241026091801-db6d9762/85/Supervised-learning-for-IOT-IN-Vellore-Institute-of-Technology-34-320.jpg)
![Contd…
• Batch gradient descent
• Computes the gradient of the cost function with respect to the
parameters w for the entire training dataset
• For a function , derivative (slope at point w) of it is
• A small change () in the input can cause the output to move to a
value given by [via first order Taylor series]
• Assuming minimization, we take a jump such that y reduces
• Gradient descent proposes weight update as
• Here is the learning rate and m is the batch-size](https://image.slidesharecdn.com/supervisedlearning-241026091801-db6d9762/85/Supervised-learning-for-IOT-IN-Vellore-Institute-of-Technology-35-320.jpg)











