Test Suite Generation for Boolean Conditions with Equivalence Class Partitioning
- 1. S. Hallé Sylvain Hallé Université du Québec à Chicoutimi CANADA Test Suite Generation for Boolean Conditions with Equivalence Class Partitioning CRSNG NSERC FormaliSE, May 2022
- 2. S. Hallé Boolean Conditions Software systems are filled with conditions that modulate their behavior. SELECT name FROM employees WHERE YEAR(dob) < 1990 AND rank = 3; if (a % 3 == 0 || (b > c + 6 && o.isReady()) { ... } Italic Bold + Underline OK Reversed + c1 a (8/1) =b ≠b (4/2) <2 >2 ⊤ ⊤ =2 c3 (7/2) =0 ≠0 (3/1) ⊤ ⊤ a ≠c =c (10/3) ⊤ (7/2) =0 ≠0 (3/1) ⊤ ⊤ c2
- 3. S. Hallé Boolean Conditions Test input generation is the problem of (automatically) generating values given to a system if (a % 3 == 0 || (b > c + 6 && o.isReady()) { ... }
- 4. S. Hallé Boolean Conditions Test input generation is the problem of (automatically) generating values given to a system if (a % 3 == 0 || (b > c + 6 && o.isReady()) { ... } a = 3 b = 2 c = 1 o.isReady() = true test case
- 5. S. Hallé Boolean Conditions Test input generation is the problem of (automatically) generating values given to a system if (a % 3 == 0 || (b > c + 6 && o.isReady()) { ... } a = 3 b = 2 c = 1 o.isReady() = true test case 1 1
- 6. S. Hallé Boolean Conditions Test input generation is the problem of (automatically) generating values given to a system if (a % 3 == 0 || (b > c + 6 && o.isReady()) { ... } a = 3 b = 2 c = 1 o.isReady() = true test case else { ... } 2 a = 1 b = 2 c = 2 o.isReady() = false 2 Different values send the execution on different paths 1 1
- 7. S. Hallé ...but what if the condition is incorrect? Boolean Conditions Test input generation is the problem of (automatically) generating values given to a system if (a % 3 == 0 || (b > c + 6 && o.isReady()) { ... } a = 3 b = 2 c = 1 o.isReady() = true test case else { ... } 2 a = 1 b = 2 c = 2 o.isReady() = false 2 Different values send the execution on different paths 1 1
- 8. S. Hallé We must generate a test input for which the condition sends the execution in the wrong branch Boolean Conditions a % 3 == 0 || (b > c + 6 && o.isReady()) a % 3 == 0 || (b ≥ c + 6 && o.isReady()) ACTUAL EXPECTED
- 9. S. Hallé a = 0 b = 6 c = 0 o.isReady() = true 4 We must generate a test input for which the condition sends the execution in the wrong branch Boolean Conditions a % 3 == 0 || (b > c + 6 && o.isReady()) a % 3 == 0 || (b ≥ c + 6 && o.isReady()) ACTUAL EXPECTED
- 10. S. Hallé a = 0 b = 6 c = 0 o.isReady() = true 4 ⊤ ⊥ ⊤ ⊤ ⊤ ⊤ ⊤ ⊤ + We must generate a test input for which the condition sends the execution in the wrong branch Boolean Conditions a % 3 == 0 || (b > c + 6 && o.isReady()) a % 3 == 0 || (b ≥ c + 6 && o.isReady()) ACTUAL EXPECTED
- 11. S. Hallé a = 0 b = 6 c = 0 o.isReady() = true a = 1 b = 7 c = 1 o.isReady() = false + 4 5 We must generate a test input for which the condition sends the execution in the wrong branch Boolean Conditions a % 3 == 0 || (b > c + 6 && o.isReady()) a % 3 == 0 || (b ≥ c + 6 && o.isReady()) ACTUAL EXPECTED
- 12. S. Hallé a = 0 b = 6 c = 0 o.isReady() = true a = 1 b = 7 c = 1 o.isReady() = false + 4 5 ⊥ ⊥ ⊥ ⊥ ⊤ ⊥ ⊥ ⊥ + We must generate a test input for which the condition sends the execution in the wrong branch Boolean Conditions a % 3 == 0 || (b > c + 6 && o.isReady()) a % 3 == 0 || (b ≥ c + 6 && o.isReady()) ACTUAL EXPECTED
- 13. S. Hallé a = 0 b = 6 c = 0 o.isReady() = true a = 1 b = 7 c = 1 o.isReady() = false + + a = 1 b = 7 c = 1 o.isReady() = true 4 5 6 We must generate a test input for which the condition sends the execution in the wrong branch Boolean Conditions a % 3 == 0 || (b > c + 6 && o.isReady()) a % 3 == 0 || (b ≥ c + 6 && o.isReady()) ACTUAL EXPECTED
- 14. S. Hallé a = 0 b = 6 c = 0 o.isReady() = true a = 1 b = 7 c = 1 o.isReady() = false + + a = 1 b = 7 c = 1 o.isReady() = true 4 5 6 ⊥ ⊥ ⊤ ⊥ ⊤ ⊤ ⊥ ⊤ ✓ We must generate a test input for which the condition sends the execution in the wrong branch Boolean Conditions a % 3 == 0 || (b > c + 6 && o.isReady()) a % 3 == 0 || (b ≥ c + 6 && o.isReady()) ACTUAL EXPECTED
- 15. S. Hallé Making the condition true/false once is not sufficient to reveal errors The components of the condition must evaluate to true/false in various combinations ⇒ Boolean condition coverage We must generate a test input for which the condition sends the execution in the wrong branch Boolean Conditions a % 3 == 0 || (b > c + 6 && o.isReady()) a % 3 == 0 || (b ≥ c + 6 && o.isReady()) ACTUAL EXPECTED
- 16. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃)
- 17. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) Predicate coverage Each variable has a test case where it is true, and another test case where it is false
- 18. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) Combinatorial ("t-way") coverage Each t-tuple of variables has test cases for all combinations of their true/false values Example: for t=2
- 19. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) Clause coverage Each clause of the condition has a test case where it is true and another test case where it is false { clause
- 20. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) Modified condition/decision coverage (MC/DC) Predicate coverage + clause coverage + every clause is shown to independently affect the outcome
- 21. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) Modified condition/decision coverage (MC/DC) Predicate coverage + clause coverage + every clause is shown to independently affect the outcome ⊥ ⊥ ⊥ ⊥ x₀ = ⊥ x₁ = ⊥ x₂ = ⊥ x₃ = ⊥
- 22. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) Modified condition/decision coverage (MC/DC) Predicate coverage + clause coverage + every clause is shown to independently affect the outcome (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) ⊥ ⊥ ⊤ ⊥ x₀ = ⊥ x₁ = ⊥ x₂ = ⊥ x₃ = ⊥ ⊤ x₀ = ⊥ x₁ = ⊤ x₂ = ⊥ x₃ = ⊤
- 23. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) MUMCUT Coverage 3 conditions expressed in terms of:
- 24. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) MUMCUT Coverage 3 conditions expressed in terms of: Unique true point (UTP): test case that makes a single clause evaluate to ⊤
- 25. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) MUMCUT Coverage 3 conditions expressed in terms of: Unique true point (UTP): test case that makes a single clause evaluate to ⊤ x₀ = ⊥ x₁ = ⊤ x₂ = ⊥ x₃ = ⊤ ⊥ ⊤ ⊥
- 26. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) MUMCUT Coverage 3 conditions expressed in terms of: Unique true point (UTP): test case that makes a single clause evaluate to ⊤ Near false point (NFP): test case where the condition is ⊥, but flipping a single variable changes its value
- 27. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) MUMCUT Coverage 3 conditions expressed in terms of: Unique true point (UTP): test case that makes a single clause evaluate to ⊤ Near false point (NFP): test case where the condition is ⊥, but flipping a single variable changes its value ⊥ ⊥ ⊥ x₀ = ⊥ x₁ = ⊥ x₂ = ⊥ x₃ = ⊤
- 28. S. Hallé Several coverage criteria for Boolean conditions have been proposed Coverage Criteria (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) MUTP: each variable not in a UTP must be true/ false in at least one test MNFP: each variable not in a NFP must be true/ false in at least one test CUTP-NFP: all pairs of UTP and NFP for the same clause that differ by a single variable flip must be present MUMCUT Coverage 1 2 3
- 29. S. Hallé Each coverage criterion is expressed informally; no uniform formal notation to define them all Each criterion comes with its own algorithm to generate test cases; the correctness/optimality of these algorithms is often not demonstrated Concrete implementations of these algorithms are not easy to find (research papers); switching criteria means switching programs Must restart from scratch if developing a new coverage criterion In the current state of things... Coverage Criteria
- 30. S. Hallé Foundations based on concepts of algebra Existing criteria become particular cases of this model Provides a test generation algorithm that works of any criterion Comes with a concrete and freely available implementation Goal: define a formal model of Boolean condition coverage Contribution
- 31. S. Hallé Algebraic Definition of Coverage Let X be a set of arbitrary symbols (variables). A valuation is a total function ν : X → {⊤,⊥}. We define as N the set of all valuations. We denote by φ[ν] the result of evaluating φ by setting its variables to the values defined by ν. Let Φ be the set of Boolean formulas with variables in X. A valuation ν ∈ N is a specific way of evaluating a condition φ ∈ Φ. Example: X = {x₀,x₁} ν(x₀) = ⊤, ν(x₁) = ⊥ φ = x₀ ∧ ¬x₁ φ[ν] = ⊤
- 32. S. Hallé Algebraic Definition of Coverage Let τ : N → C be a total function mapping each valuation ν to an element of a set C. An element c ∈ C is called a category. Intuitively, τ classifies valuations into categories; we call it a categorization function. Two valuations ν and ν' are in the same equivalence class if τ(ν) = τ(ν'). We note this ν ~ ν'. The kernel of τ is the partition of N induced by the quotient N/~. Each subset contains the valuations that belong to the same category. algebra!
- 33. S. Hallé Algebraic Definition of Coverage Example X = {x₀,x₁} There are 4 valuations in N: ν₀ = {x₀ ↦ ⊤, x₁ ↦ ⊤} ν₁ = {x₀ ↦ ⊤, x₁ ↦ ⊥} ν₂ = {x₀ ↦ ⊥, x₁ ↦ ⊤} ν₃ = {x₀ ↦ ⊥, x₁ ↦ ⊥}
- 34. S. Hallé Define τ : N → {0,1} as τ(ν) ={0 if ν(x₀) = ⊤ 1 otherwise Algebraic Definition of Coverage Example X = {x₀,x₁} There are 4 valuations in N: ν₀ = {x₀ ↦ ⊤, x₁ ↦ ⊤} ν₁ = {x₀ ↦ ⊤, x₁ ↦ ⊥} ν₂ = {x₀ ↦ ⊥, x₁ ↦ ⊤} ν₃ = {x₀ ↦ ⊥, x₁ ↦ ⊥}
- 35. S. Hallé Define τ : N → {0,1} as τ(ν) ={0 if ν(x₀) ≠ ν(x₁) 1 otherwise Algebraic Definition of Coverage Example X = {x₀,x₁} There are 4 valuations in N: ν₀ = {x₀ ↦ ⊤, x₁ ↦ ⊤} ν₁ = {x₀ ↦ ⊤, x₁ ↦ ⊥} ν₂ = {x₀ ↦ ⊥, x₁ ↦ ⊤} ν₃ = {x₀ ↦ ⊥, x₁ ↦ ⊥}
- 36. S. Hallé Define τ : N → {0,1} as τ(ν) = the number of true variables in ν 2 1 0 Algebraic Definition of Coverage Example X = {x₀,x₁} There are 4 valuations in N: ν₀ = {x₀ ↦ ⊤, x₁ ↦ ⊤} ν₁ = {x₀ ↦ ⊤, x₁ ↦ ⊥} ν₂ = {x₀ ↦ ⊥, x₁ ↦ ⊤} ν₃ = {x₀ ↦ ⊥, x₁ ↦ ⊥}
- 37. S. Hallé ECP: methodology where test cases are divided in partitions Equivalence Class Partitioning
- 38. S. Hallé Set of all possible test cases ECP: methodology where test cases are divided in partitions Equivalence Class Partitioning
- 39. S. Hallé Set of all possible test cases Equivalence classes ECP: methodology where test cases are divided in partitions Equivalence Class Partitioning
- 40. S. Hallé Set of all possible test cases Equivalence classes ECP: methodology where test cases are divided in partitions Equivalence Class Partitioning Chosen test cases
- 41. S. Hallé ECP: methodology where test cases are divided in partitions Equivalence Class Partitioning Set of all possible valuations (N) Equivalence classes induced by τ Representatives
- 42. S. Hallé Algebraic Definition of Coverage A test suite is a set of valuations (i.e. an element V ∈ 2 ). N Define 𝜏(V) = ⋃ 𝜈 ∈ V {𝜏(𝜈)} "the set of categories present in the test suite" A Boolean condition coverage criterion is called algebraic if... for every Boolean formula 𝜑, there exists a function 𝜏, such that a test suite V satisfies the criterion if and only if 𝜏(V) = 𝜏(N). "all categories are represented in V"
- 43. S. Hallé 𝜌(V) ∈ [0,1], and full coverage means 𝜌(V) = 1. Algebraic Definition of Coverage If a test suite V achieves partial coverage, it can easily be quantified: 𝜌(V) = 𝜏(V) 𝜏(N) coverage ratio of V fraction of all categories that are present in V Note that we did not need to specify what specific criterion we are talking about!
- 44. S. Hallé Evaluation Trees ∧ ∨ ¬ a ¬ c b ∨ ¬ b c φ = (a ∨ ¬b ∨ c) ∧ ¬(¬c ∨ b) A valuation ν applied on a formula φ induces a structure called an evaluation tree.
- 45. S. Hallé ν = {a ↦ ⊤, b ↦ ⊥, c ↦ ⊤} Each valuation "colors" the structure differently Each combination of ν and φ produces a unique tree Define as eν(φ) the function that produces the evaluation tree of φ[ν]. Evaluation Trees ∧ ∨ ¬ a ¬ c b ∨ ¬ b c φ = (a ∨ ¬b ∨ c) ∧ ¬(¬c ∨ b) A valuation ν applied on a formula φ induces a structure called an evaluation tree.
- 46. S. Hallé Tree Transformation Let T be the set of trees. We define T* as the set of trees where nodes can be labeled with . A tree transformation is a function 𝜏 : T* → T* that turns an evaluation tree into another one. Since trees are obtained by evaluating formulas, we let 𝜏ν : Φ → T* be the function such that ? ^ 𝜏ν(φ) = 𝜏(eν(φ)) ^ i.e. for a valuation ν, 𝜏ν gets the evaluation tree for φ and applies the transformation 𝜏 to it. ^
- 47. S. Hallé Tree Transformation We are free to define 𝜏 as we want. ∨ ∧ ∧ ∧ a ¬ c b ¬ ¬ a b ¬ b ¬ a c
- 48. S. Hallé Tree Transformation We are free to define 𝜏 as we want. ∨ ∧ ∧ ∧ a ¬ c b ¬ ¬ a b ¬ b ¬ a c ∨ ∧ Keep only the root and its immediate children. ∧ ∧
- 49. S. Hallé Tree Transformation We are free to define 𝜏 as we want. ∨ ∧ ∧ ∧ a ¬ c b ¬ ¬ a b ¬ b ¬ a c ∨ ? ∧ ? Turn every child of the root, except the second, into , and trim the descendants of the second node. ?
- 50. S. Hallé Tree Transformation We are free to define 𝜏 as we want. ∨ ∧ ∧ ∧ a ¬ c b ¬ ¬ a b ¬ b ¬ a c Put under the root a leaf labelled a and a leaf labelled b, in that order. ∨ a b
- 51. S. Hallé Tree Transformation We are free to define 𝜏 as we want. ∨ ∧ ∧ ∧ a ¬ c b ¬ ¬ a b ¬ b ¬ a c Under every connective node, keep only subtrees until the first that determines its color ∨ ∧ ∧ ∧ a ¬ c b ¬ ¬ a b ¬ b ¬ a c
- 52. S. Hallé Tree Transformation For a given formula φ, some tree transformations map more than one valuation to the same tree. ∧ ∨ ¬ a ¬ c b ∨ ¬ b c φ 𝜏 = keep only the root and its immediate children = (a ∨ ¬b ∨ c) ∧ ¬(¬c ∨ b)
- 53. S. Hallé Tree Transformation For a given formula φ, some tree transformations map more than one valuation to the same tree. ∧ ∨ ¬ a ¬ c b ∨ ¬ b c φ 𝜏 = keep only the root and its immediate children = (a ∨ ¬b ∨ c) ∧ ¬(¬c ∨ b) ∧ ∨ ¬ {a ↦ ⊥, b ↦ ⊤, c ↦ ⊥} ^ 𝜏
- 54. S. Hallé Tree Transformation For a given formula φ, some tree transformations map more than one valuation to the same tree. ∧ ∨ ¬ a ¬ c b ∨ ¬ b c φ 𝜏 = keep only the root and its immediate children = (a ∨ ¬b ∨ c) ∧ ¬(¬c ∨ b) ∧ ∨ ¬ {a ↦ ⊥, b ↦ ⊤, c ↦ ⊥} ^ 𝜏 {a ↦ ⊥, b ↦ ⊥, c ↦ ⊤} {a ↦ ⊤, b ↦ ⊥, c ↦ ⊤} ∧ ∨ ¬ ^ 𝜏
- 55. S. Hallé Tree Transformation For a given formula φ, some tree transformations map more than one valuation to the same tree. ∧ ∨ ¬ a ¬ c b ∨ ¬ b c φ 𝜏 = keep only the root and its immediate children = (a ∨ ¬b ∨ c) ∧ ¬(¬c ∨ b) ∧ ∨ ¬ {a ↦ ⊥, b ↦ ⊤, c ↦ ⊥} ^ 𝜏 {a ↦ ⊥, b ↦ ⊥, c ↦ ⊤} {a ↦ ⊤, b ↦ ⊥, c ↦ ⊤} ∧ ∨ ¬ ^ 𝜏 ∧ ∨ ¬ ^ 𝜏 {a ↦ ⊥, b ↦ ⊥, c ↦ ⊥} {a ↦ ⊥, b ↦ ⊤, c ↦ ⊤} {a ↦ ⊤, b ↦ ⊥, c ↦ ⊥} {a ↦ ⊤, b ↦ ⊤, c ↦ ⊥} {a ↦ ⊤, b ↦ ⊤, c ↦ ⊤}
- 56. S. Hallé Tree Transformation Key observation: for a given formula, a tree transformation partitions the set of valuations according to the tree each is mapped to... ∧ ∨ ¬ ∧ ∨ ¬ {⊥⊥⊤,⊤⊥⊤} ∅ ∧ ∨ ¬ ∧ ∨ ¬ {⊥⊥⊥,⊥⊤⊤, ⊤⊥⊥,⊤⊤⊥,⊤⊤⊤} {⊥⊤⊥} ⇒ it defines an algebraic coverage criterion!
- 57. S. Hallé 1. Questions Are the coverage criteria mentioned earlier algebraic? 2. If so, can we find a tree transformation for each that results in the same partitioning of the test input space?
- 58. S. Hallé 1. Questions Are the coverage criteria mentioned earlier algebraic? 2. If so, can we find a tree transformation for each that results in the same partitioning of the test input space? YES (except MUMCUT*) *An over-approximation is shown to be algebraic
- 59. S. Hallé 1. Questions Are the coverage criteria mentioned earlier algebraic? 2. If so, can we find a tree transformation for each that results in the same partitioning of the test input space? YES (except MUMCUT*) *An over-approximation is shown to be algebraic YES (all details in the paper)
- 60. S. Hallé Define 𝜏ₙ as: An Example Turn the root and every child of the root, except the n-th, into , and trim the descendants of the n-th node. ?
- 61. S. Hallé Define 𝜏ₙ as: An Example Turn the root and every child of the root, except the n-th, into , and trim the descendants of the n-th node. ? (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) Valuations are classified by 𝜏ₙ depending on the value they give to the n-th clause. n=2 ? ∧ ? ? ∧ ? ? ? ? ∧ ? ? ∧ ? ? ? n=1 ? ∧ ? ? ∧ ? ? ? n=3
- 62. S. Hallé Define 𝜏ₙ as: An Example Turn the root and every child of the root, except the n-th, into , and trim the descendants of the n-th node. ? (x₀ ∧ ¬x₁ ∧ x₂) ∨ (x₁ ∧ x₃) ∨ (¬x₀ ∧ x₂ ∧ x₃) Valuations are classified by 𝜏ₙ depending on the value they give to the n-th clause. n=2 ? ∧ ? ? ∧ ? ? ? ? ∧ ? ? ∧ ? ? ? n=1 ? ∧ ? ? ∧ ? ? ? n=3 One valuation for each tree ⇒ clause coverage
- 63. S. Hallé We define appropriate transformations for all coverage criteria shown earlier... except MUMCUT. A Word About MUMCUT MUTP: each variable not in a UTP must be true/ false in at least one test MNFP: each variable not in a NFP must be true/ false in at least one test CUTP-NFP: all pairs of UTP and NFP for the same clause that differ by a single variable flip must be present MUMCUT Coverage 1 2 3
- 64. S. Hallé ✓ algebraic ✓ algebraic not algebraic? ? We define appropriate transformations for all coverage criteria shown earlier... except MUMCUT. A Word About MUMCUT MUTP: each variable not in a UTP must be true/ false in at least one test MNFP: each variable not in a NFP must be true/ false in at least one test CUTP-NFP: all pairs of UTP and NFP for the same clause that differ by a single variable flip must be present MUMCUT Coverage 1 2 3
- 65. S. Hallé ✓ algebraic ✓ algebraic not algebraic? ? CUTP-NFP is defined on pairs of valuations, and not on individual valuations We define appropriate transformations for all coverage criteria shown earlier... except MUMCUT. A Word About MUMCUT MUTP: each variable not in a UTP must be true/ false in at least one test MNFP: each variable not in a NFP must be true/ false in at least one test CUTP-NFP: all pairs of UTP and NFP for the same clause that differ by a single variable flip must be present MUMCUT Coverage 1 2 3
- 66. S. Hallé Generating Test Suites A test suite for any algebraic criterion can be obtained using the equivalence class partitioning method. A possible way is using a hypergraph.
- 67. S. Hallé Generating Test Suites A test suite for any algebraic criterion can be obtained using the equivalence class partitioning method. A possible way is using a hypergraph. ⊥⊥⊤ ⊥⊥⊥ ⊥⊤⊤ ⊤⊥⊥ ⊤⊤⊥ ⊤⊤⊤ ⊥⊤⊥ ⊤⊥⊤ 1. Create one node for each valuation
- 68. S. Hallé Generating Test Suites A test suite for any algebraic criterion can be obtained using the equivalence class partitioning method. A possible way is using a hypergraph. ∧ ∨ 1 ∧ ∨ 2 ∧ ∨ 3 a 4 a 5 3 4 4 4 5 5 5 1 2 2 2 2 2. Add one hyperedge linking the nodes mapped to each tree induced by 𝜏 ⊥⊥⊤ ⊥⊥⊥ ⊥⊤⊤ ⊤⊥⊥ ⊤⊤⊥ ⊤⊤⊤ ⊥⊤⊥ ⊤⊥⊤ 1. Create one node for each valuation
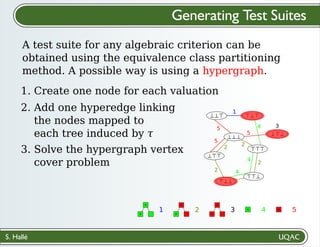
- 69. S. Hallé Generating Test Suites A test suite for any algebraic criterion can be obtained using the equivalence class partitioning method. A possible way is using a hypergraph. ∧ ∨ 1 ∧ ∨ 2 ∧ ∨ 3 a 4 a 5 3 4 4 4 5 5 5 1 2 2 2 2 2. Add one hyperedge linking the nodes mapped to each tree induced by 𝜏 ⊥⊥⊤ ⊥⊥⊥ ⊥⊤⊤ ⊤⊥⊥ ⊤⊤⊥ ⊤⊤⊤ ⊥⊤⊥ ⊤⊥⊤ 1. Create one node for each valuation 3. Solve the hypergraph vertex cover problem
- 70. S. Hallé Generating Test Suites A test suite for any algebraic criterion can be obtained using the equivalence class partitioning method. A possible way is using a hypergraph. ∧ ∨ 1 ∧ ∨ 2 ∧ ∨ 3 a 4 a 5 3 4 4 4 5 5 5 1 2 2 2 2 2. Add one hyperedge linking the nodes mapped to each tree induced by 𝜏 ⊥⊥⊤ ⊥⊥⊥ ⊥⊤⊤ ⊤⊥⊥ ⊤⊤⊥ ⊤⊤⊤ ⊥⊤⊥ ⊤⊥⊤ 1. Create one node for each valuation 3. Solve the hypergraph vertex cover problem The selected nodes form the test suite.
- 71. S. Hallé Generating Test Suites Cons The hypergraph has 2|X| nodes The vertex cover problem has a high complexity Pros Guarantees full coverage for any algebraic criterion Optimal hypergraph cover ⇔ optimal test suite Upper bound on complexity Can solve for multiple criteria at once (instead of separately + merging)
- 72. S. Hallé Boolean Coverage Toolkit These principles have been concretely implemented in an open source Java library: https://github.com/liflab/boolean-coverage-toolkit Operator o = Or(And(a, Not(b), c), And(Not(a), Not(b)), And(Not(a), b, Not(c))); HologramNode n1 = o.evaluate(new Valuation(false, false, true)); Truncation t = new FailFast(2); HologramNode n2 = t.applyTo(n1); Set<Truncation> set = new HashSet<>(); set.add(new KeepTop(2)); set.add(new KeepVariable(a)); HypergraphGenerator g = new HypergraphGenerator(); Hypergraph h = g.getGraph(o, set); Iterator<?> it = HittingSetRunner.runHittingSet(h).iterator(); while (it.hasNext()) { Valuation v = g.getValuation(it.next()); }
- 73. S. Hallé Create Boolean condition Boolean Coverage Toolkit These principles have been concretely implemented in an open source Java library: https://github.com/liflab/boolean-coverage-toolkit Operator o = Or(And(a, Not(b), c), And(Not(a), Not(b)), And(Not(a), b, Not(c))); HologramNode n1 = o.evaluate(new Valuation(false, false, true)); Truncation t = new FailFast(2); HologramNode n2 = t.applyTo(n1); Set<Truncation> set = new HashSet<>(); set.add(new KeepTop(2)); set.add(new KeepVariable(a)); HypergraphGenerator g = new HypergraphGenerator(); Hypergraph h = g.getGraph(o, set); Iterator<?> it = HittingSetRunner.runHittingSet(h).iterator(); while (it.hasNext()) { Valuation v = g.getValuation(it.next()); }
- 74. S. Hallé Create Boolean condition Obtain an expression tree and apply a transformation Boolean Coverage Toolkit These principles have been concretely implemented in an open source Java library: https://github.com/liflab/boolean-coverage-toolkit Operator o = Or(And(a, Not(b), c), And(Not(a), Not(b)), And(Not(a), b, Not(c))); HologramNode n1 = o.evaluate(new Valuation(false, false, true)); Truncation t = new FailFast(2); HologramNode n2 = t.applyTo(n1); Set<Truncation> set = new HashSet<>(); set.add(new KeepTop(2)); set.add(new KeepVariable(a)); HypergraphGenerator g = new HypergraphGenerator(); Hypergraph h = g.getGraph(o, set); Iterator<?> it = HittingSetRunner.runHittingSet(h).iterator(); while (it.hasNext()) { Valuation v = g.getValuation(it.next()); }
- 75. S. Hallé Create Boolean condition Obtain an expression tree and apply a transformation Create tree transformations Boolean Coverage Toolkit These principles have been concretely implemented in an open source Java library: https://github.com/liflab/boolean-coverage-toolkit Operator o = Or(And(a, Not(b), c), And(Not(a), Not(b)), And(Not(a), b, Not(c))); HologramNode n1 = o.evaluate(new Valuation(false, false, true)); Truncation t = new FailFast(2); HologramNode n2 = t.applyTo(n1); Set<Truncation> set = new HashSet<>(); set.add(new KeepTop(2)); set.add(new KeepVariable(a)); HypergraphGenerator g = new HypergraphGenerator(); Hypergraph h = g.getGraph(o, set); Iterator<?> it = HittingSetRunner.runHittingSet(h).iterator(); while (it.hasNext()) { Valuation v = g.getValuation(it.next()); }
- 76. S. Hallé Create Boolean condition Obtain an expression tree and apply a transformation Create tree transformations Generate and solve hypergraph Boolean Coverage Toolkit These principles have been concretely implemented in an open source Java library: https://github.com/liflab/boolean-coverage-toolkit Operator o = Or(And(a, Not(b), c), And(Not(a), Not(b)), And(Not(a), b, Not(c))); HologramNode n1 = o.evaluate(new Valuation(false, false, true)); Truncation t = new FailFast(2); HologramNode n2 = t.applyTo(n1); Set<Truncation> set = new HashSet<>(); set.add(new KeepTop(2)); set.add(new KeepVariable(a)); HypergraphGenerator g = new HypergraphGenerator(); Hypergraph h = g.getGraph(o, set); Iterator<?> it = HittingSetRunner.runHittingSet(h).iterator(); while (it.hasNext()) { Valuation v = g.getValuation(it.next()); }
- 77. S. Hallé Create Boolean condition Obtain an expression tree and apply a transformation Create tree transformations Generate and solve hypergraph Iterate over valuations of the solution Boolean Coverage Toolkit These principles have been concretely implemented in an open source Java library: https://github.com/liflab/boolean-coverage-toolkit Operator o = Or(And(a, Not(b), c), And(Not(a), Not(b)), And(Not(a), b, Not(c))); HologramNode n1 = o.evaluate(new Valuation(false, false, true)); Truncation t = new FailFast(2); HologramNode n2 = t.applyTo(n1); Set<Truncation> set = new HashSet<>(); set.add(new KeepTop(2)); set.add(new KeepVariable(a)); HypergraphGenerator g = new HypergraphGenerator(); Hypergraph h = g.getGraph(o, set); Iterator<?> it = HittingSetRunner.runHittingSet(h).iterator(); while (it.hasNext()) { Valuation v = g.getValuation(it.next()); }
- 78. S. Hallé Experiments We can compare the hypergraph-based approach with existing tools and techniques: Random selection ACTS (combinatorial coverage) mcdc (MC/DC coverage) and results published in past papers (implementation unavailable).
- 79. S. Hallé Experiments Test suite size 0 2 4 6 8 10 12 14 2 4 6 8 10 12 14 Hypergraph MCDC SAT 0 200 400 600 800 1000 1200 1400 1600 1800 0 200 400 600 800 1000 1200 1400 1600 1800 Hypergraph Chen G-CUN MC/DC MUMCUT The hypergraph approach generates test suites of comparable size for MC/DC, but larger for MUMCUT (over-approximated)
- 80. S. Hallé Experiments Solving for two criteria at once Criteria Size ratio Time ratio MC/DC + Clause MC/DC + Predicate MC/DC + MUMCUT MC/DC + 2-way MC/DC + 3-way Clause + 2-way Clause + 3-way 0.87 0.85 0.99 0.76 0.83 0.83 0.87 1.27 1.29 1.38 1.20 1.11 1.24 1.11 The hypergraph approach takes more time, but produces smaller test suites than when two independent solutions are merged
- 81. S. Hallé Conclusion Uniform theoretical framework to define coverage criteria as equivalence classes induced by a tree transformation Generic algorithm to produce test suites according to any algebraic coverage criterion Opens the way to experiments with new coverage criteria and benchmarking of existing ones. Future work: extension to other logics, such as temporal/description logics































![S. Hallé
Algebraic Definition of Coverage
Let X be a set of arbitrary symbols (variables). A
valuation is a total function ν : X → {⊤,⊥}. We
define as N the set of all valuations.
We denote by φ[ν] the result of evaluating φ by
setting its variables to the values defined by ν.
Let Φ be the set of Boolean formulas with variables
in X. A valuation ν ∈ N is a specific way of
evaluating a condition φ ∈ Φ.
Example: X = {x₀,x₁}
ν(x₀) = ⊤, ν(x₁) = ⊥
φ = x₀ ∧ ¬x₁
φ[ν] = ⊤](https://image.slidesharecdn.com/slides-220518132747-38bedf5e/85/Test-Suite-Generation-for-Boolean-Conditions-with-Equivalence-Class-Partitioning-31-320.jpg)











![S. Hallé
𝜌(V) ∈ [0,1], and full coverage means 𝜌(V) = 1.
Algebraic Definition of Coverage
If a test suite V achieves partial coverage, it can
easily be quantified:
𝜌(V) =
𝜏(V)
𝜏(N)
coverage ratio of V fraction of all
categories that are
present in V
Note that we did not need to specify what specific
criterion we are talking about!](https://image.slidesharecdn.com/slides-220518132747-38bedf5e/85/Test-Suite-Generation-for-Boolean-Conditions-with-Equivalence-Class-Partitioning-43-320.jpg)

![S. Hallé
ν = {a ↦ ⊤, b ↦ ⊥, c ↦ ⊤}
Each valuation "colors" the
structure differently
Each combination of ν and φ
produces a unique tree
Define as eν(φ) the function that produces
the evaluation tree of φ[ν].
Evaluation Trees
∧
∨ ¬
a ¬ c
b
∨
¬ b
c
φ = (a ∨ ¬b ∨ c) ∧ ¬(¬c ∨ b)
A valuation ν applied on a formula φ induces a
structure called an evaluation tree.](https://image.slidesharecdn.com/slides-220518132747-38bedf5e/85/Test-Suite-Generation-for-Boolean-Conditions-with-Equivalence-Class-Partitioning-45-320.jpg)