![Example
• English
• Alphabet – [a-z]
• String –{hi,hello,…}
• Binary number
• Alphabet – [0,1]
• String –{0,1,00,01,10,11…}
• Hexadecimal
• Alphabet –[0-9][a-e]
• String –[0,1,1A3,…]
16
Mrs.D.Jena
Catherine
Bel,
AP/CSE,
VEC](https://image.slidesharecdn.com/fullunit1-220307085807/85/Theory-of-Computation-Unit-1-16-320.jpg)
![Now we will obtain δ' transition for state q0.
δ'([q0], 0) = [q0]
δ'([q0], 1) = [q1]
The δ' transition for state q1 is obtained as:
δ'([q1], 0) = [q1, q2] (new state generated)
δ'([q1], 1) = [q1]
84
Mrs.D.Jena
Catherine
Bel,
AP/CSE,
VEC](https://image.slidesharecdn.com/fullunit1-220307085807/85/Theory-of-Computation-Unit-1-84-320.jpg)
![Now we will obtain δ' transition on [q1, q2].
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0)
= {q1, q2} ∪ {q2}
= [q1, q2]
δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1)
= {q1} ∪ {q1, q2}
= {q1, q2}
= [q1, q2]
The state [q1, q2] is the final state as well because
it contains a final state q2. 85
Mrs.D.Jena
Catherine
Bel,
AP/CSE,
VEC](https://image.slidesharecdn.com/fullunit1-220307085807/85/Theory-of-Computation-Unit-1-85-320.jpg)
![State 0 1
→[q0] [q0] [q1]
[q1] [q1, q2] [q1]
*[q1, q2] [q1, q2] [q1, q2]
The transition table for the constructed DFA will
be:
86
Mrs.D.Jena
Catherine
Bel,
AP/CSE,
VEC](https://image.slidesharecdn.com/fullunit1-220307085807/85/Theory-of-Computation-Unit-1-86-320.jpg)
Theory of Computation Unit 1
- 1. THEORY OF COMPUTATION Sub Code: CS8501 Credit : 3 Mrs.D.Jena Catherine Bel Assistant Professor, CSE Velammal Engineering College
- 2. Course Objective The student should be made to: • To understand the language hierarchy • To construct automata for any given pattern and find its equivalent regular expressions • To design a context free grammar for any given language • To understand Turing machines and their capability • To understand undecidable problems and NP class problems Mrs.D.Jena Catherine Bel, AP/CSE, VEC 2
- 3. Theory of Computation • What? • The theory of computation is a branch of computer science and mathematics combined • deals with how efficiently problems can be solved on a model of computation, using an algorithm. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 3
- 4. Application • Where? • Text processing • Compilers • Programming Languages • Artificial Intelligence • Genetic programming • Neural Networks • Robotics Mrs.D.Jena Catherine Bel, AP/CSE, VEC 4
- 7. UNIT I AUTOMATA FUNDAMENTALS Introduction to formal proof – Additional forms of Proof – Inductive Proofs –Finite Automata – Deterministic Finite Automata – Non-deterministic Finite Automata – Finite Automata with Epsilon Transitions Mrs.D.Jena Catherine Bel, AP/CSE, VEC 7
- 8. UNIT II REGULAR EXPRESSIONS AND LANGUAGES Regular Expressions – FA and Regular Expressions – Proving Languages not to be regular – Closure Properties of Regular Languages – Equivalence and Minimization of Automata. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 8
- 9. UNIT III CONTEXT FREE GRAMMAR AND LANGUAGES CFG – Parse Trees – Ambiguity in Grammars and Languages – Definition of the Pushdown Automata – Languages of a Pushdown Automata – Equivalence of Pushdown Automata and CFG, Deterministic Pushdown Automata. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 9
- 10. UNIT IV PROPERTIES OF CONTEXT FREE LANGUAGES Normal Forms for CFG – Pumping Lemma for CFL – Closure Properties of CFL – Turing Machines – Programming Techniques for TM. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 10
- 11. UNIT V UNDECIDABILITY Non Recursive Enumerable (RE) Language – Undecidable Problem with RE – Undecidable Problems about TM – Post‘s Correspondence Problem, The Class P and NP. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 11
- 12. Course Outcome At the end of the course, the students will be able to: 1. Design of Finite State Machine for any pattern (Unit 1) 2. Design of regular expression for any pattern and analyze the properties of regular languages (Unit 2) 3. Write Context free grammar for any construct and design of Pushdown Automata (Unit 3) 4. Apply Normal forms of CFG and analyze the properties of CFG (Unit 4) 5. Design Turing machines for any language and Propose computation solutions using Turing machines(Unit 4) 6. Derive whether a problem is decidable or not.(Unit 5) Mrs.D.Jena Catherine Bel, AP/CSE, VEC 12
- 13. Text Books 1. J.E.Hopcroft, R.Motwani and J.D Ullman, ―Introduction to Automata Theory, Languages and Computations, Second Edition, Pearson Education, 2003. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 13
- 14. Reference Books 1. H.R.Lewis and C.H.Papadimitriou, ―Elements of the theory of Computation, Second Edition, PHI, 2003. 2. J.Martin, ―Introduction to Languages and the Theory of Computation, Third Edition, TMH, 2003. 3. Micheal Sipser, ―Introduction of the Theory and Computation, Thomson Brokecole, 1997. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 14
- 15. Terminologies • Alphabet • Finite, non empty set of symbols • Basic elements of a language • Denoted by ∑ • String • Finite sequence of symbols chosen from some alphabets • Empty string • Length of the string • Power of an alphabet • Language • Set of all strings which are chosen from ∑* 15 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 16. Example • English • Alphabet – [a-z] • String –{hi,hello,…} • Binary number • Alphabet – [0,1] • String –{0,1,00,01,10,11…} • Hexadecimal • Alphabet –[0-9][a-e] • String –[0,1,1A3,…] 16 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 19. UNIT I INTRODUCTION TO AUTOMATA Introduction to formal proof – Deductive proofs–Additional forms of Proof – Contrapositive – Proof by contradictions – Counterexamples –Inductive Proofs–Deterministic Finite Automata – Non-deterministic Finite Automata – Finite Automata with Epsilon Transitions – Formal Definition – Extended Transition function – Language of Finite Automata – Interconversion of Finite automata Mrs.D.Jena Catherine Bel, AP/CSE, VEC 19
- 20. Introduction to formal proof – Additional forms of Proof – Inductive Proofs
- 21. Introduction to Formal Proof • Deductive Proof • Reduction to definition • Other theorem forms • Theorem that appear not to be if-then statements Mrs.D.Jena Catherine Bel, AP/CSE, VEC 21
- 22. Deductive Proof • A deductive proof consists of a sequence of statements whose truth leads us from some initial statement called the hypothesis or the given statement(s) to a conclusion statement. • Each step in the proof must follow by some accepted logical principle from either the given facts or some of the previous statement • The hypothesis may be true or false, depending on the value of its parameter • If H then C . C is deducted from H Mrs.D.Jena Catherine Bel, AP/CSE, VEC 22
- 23. • Hypothesis : x ≥ 4 • Conclusion : 2x ≥ x2 • Parameter : x • Proof: • If x=3, then 23 ≥ 32 8 ≥ 9 which is false • If x=4 then 24 ≥ 42 16 ≥ 16 which is true • For each time x increments by 1, the LHS get incremented by 2 and the RHS 𝑥+1 𝑥 2 • If x ≥ 4, the 𝑥+1 𝑥 = 1.25, (1.25)2= 1.5625 • 1.5625 is less than 2 • Hence 2x ≥ x2 will be true for x ≥ 4 Mrs.D.Jena Catherine Bel, AP/CSE, VEC 23
- 24. If x is the sum of the squares of four positive integers, then 2x ≥ x2 Mrs.D.Jena Catherine Bel, AP/CSE, VEC 24
- 25. Reduction to Definitions • Convert all the terms in hypothesis to their definitions • Deductive proof Mrs.D.Jena Catherine Bel, AP/CSE, VEC 25
- 26. Let S be a finite subset of some infinite set U. Let T be the complement of S with respect to U. Then T is infinite • Let us assume T is finite, |T| = m • As per the given statement, S is finite => |S|=n • Then |S U T | = n+ m, which is finite which contradicts the given statement, Hence T should be infinite. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 26
- 27. Other Theorem Forms • Ways of saying If-Then • H implies C • H only if C • C if H • Whenever H holds, C follows • If and only if statement • A if and only if B • If part : If B then A • Only if part: If A then B Mrs.D.Jena Catherine Bel, AP/CSE, VEC 27
- 28. Theorem that appear not to be If- Then Statement • Example 𝑎 2 + 𝑏 2 = 𝑐 2 sin 𝛼 ± sin 𝛽 = 2 sin 1 2 𝛼 ± 𝛽 cos 1 2 𝛼 ∓ 𝛽 Mrs.D.Jena Catherine Bel, AP/CSE, VEC 28
- 29. Additional Forms of Proof • Proofs by sets • Proof by Contrapositive • Proofs by contradiction • Proofs by counterexample Mrs.D.Jena Catherine Bel, AP/CSE, VEC 29
- 30. Proofs by sets R U (S ∩ T) = (R U S) ∩ (R U T) Mrs.D.Jena Catherine Bel, AP/CSE, VEC 30
- 32. Proof by Contrapositive • The contrapositive of a statement negates the conclusion as well as the hypothesis. It is logically equivalent to the original statement asserted. Often it is easier to prove the contrapositive than the original statement. • If H then C is equivalent to If not C then not H • Example: • If x ≥ 4 then 2x ≥ x2 • If not 2x ≥ x2 then not x ≥ 4 • If 2x < x2 then x < 4 Mrs.D.Jena Catherine Bel, AP/CSE, VEC 32
- 33. Proofs by contradiction • The method of proof by contradiction is to assume that a statement is not true and then to show that that assumption leads to a contradiction. • To prove if H then C is to prove If H then not C implies falsehood. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 33
- 34. Proofs by counterexample • A proof by counterexample is not technically a proof. It is merely a way of showing that a given statement cannot possibly be correct by showing an instance that contradicts a universal statement. • If integer x is a prime then x is odd Mrs.D.Jena Catherine Bel, AP/CSE, VEC 34
- 35. Inductive Proof • Induction on integers • Structural induction • Mutual induction Mrs.D.Jena Catherine Bel, AP/CSE, VEC 35
- 36. Induction on integers • Mathematical Induction is a mathematical technique which is used to prove a statement, a formula or a theorem is true for every natural number. • The technique involves two steps to prove a statement, as stated below − • Step 1(Base step) − It proves that a statement is true for the initial value. • Step 2(Inductive step) − It proves that if the statement is true for the nth iteration (or number n), then it is also true for (n+1)th iteration ( or number n+1). Mrs.D.Jena Catherine Bel, AP/CSE, VEC 36
- 37. 1 + 2 + ... + n = n(n+1)/2 Proof. (Proof by Mathematical Induction) Let's let P(n) be the statement "1 + 2 + ... + n = (n (n+1)/2." Basis Step. P(1) asserts "1 = 1(2)/2", which is clearly true. So we are done with the initial step. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 37
- 38. Inductive Step. Induction Hypothesis/ Inductive assumption: Assume, 1 + 2 + ... + k = k (k+1)/2 is true Prove for k+1, (i.e) 1 + 2 + ... + k + (k+1) = (k+1)(k+2)/2. 1 + 2 + ... + k + (k+1) = k(k+1)/2 + (k+1) = (k(k+1) + 2 (k+1))/2 = (k+1)(k+2)/2. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 38
- 41. Structural Induction • Structural induction is a proof methodology similar to mathematical induction, only instead of working in the domain of positive integers (N) it works in the domain of such recursively defined structures! • It is terrifically useful for proving properties of such structures. • Its structure is sometimes “looser” than that of mathematical induction. Mrs.D.Jena Catherine Bel, AP/CSE, VEC 41
- 42. Everytree has one more nodethan its edges • If T is a tree and T has n nodes and e edges then n=e+1 • Basis: • T is single node tree, then n=1, e=0, so n=e+1 holds true • Inductive Hypothesis: • Assume the statement S(Ti ) hold for i=1,2,3,…,K and Ti have ni nodes and ei edges then ni = ei + 1 • Induction Mrs.D.Jena Catherine Bel, AP/CSE, VEC 42
- 44. Every expressionhasanequalnumberofleftand right parentheses • Let G is an expression • Basis : • G is a number or variable, so the number of left and right parenthesis is 0 • Inductive Hypothesis: • Assume E and F are two expressions which has equal number of left and right parentheses. • Induction : Mrs.D.Jena Catherine Bel, AP/CSE, VEC 44
- 49. Finite Automata • Finite automata are used to recognize patterns. • It takes the string of symbol as input and changes its state accordingly. When the desired symbol is found, then the transition occurs. • At the time of transition, the automata can either move to the next state or stay in the same state. • Finite automata have two states, Accept state or Reject state. When the input string is processed successfully, and the automata reached its final state, then it will accept. 49 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 50. • Input Tape • It is a linear tape having some number of cells. Each input symbol is placed in each cell. • Finite control • It decides the next state on receiving particular input from input tape. • Tape reader • It reads the cells one by one from left to right, and at a time only one input symbol is read. 50 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 51. • A finite automaton consists of: • a finite set S of N states • a special start state • a set of final (or accepting) states • a set of transitions T from one state to another, labelled with chars in C 51 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 52. • Execution of FA on an input sequence as follows: • Begin in the start state • If the next input char matches the label on a transition from the current state to a new state, go to that new state • Continue making transitions on each input char • If no move is possible, then stop • If in accepting state, then accept 52 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 53. Deterministic Finite Automata • Deterministic refers to the uniqueness of the computation. • On each input there is one and only one state to which the automaton can transition from its current state • DFA does not accept the null move. 53 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 54. Formal Definition of DFA • A deterministic finite automaton (DFA) is a 5-tuple (Q,Σ,δ,q0,F),where • Q is a finite set called the states, • Σ is a finite set called the alphabet, • δ:Q×Σ→Q is the transition function, • q0 ∈ Q is the start state, and • F ⊆ Q is the set of accepting states. 54 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 55. Transition Table • A transition table is a tabular representation of the transition function that takes two arguments and returns a state. • The column contains the state in which the automaton will be on the input represented by that column. • The row corresponds to the state the finite control unit can be in. • The entry for one row corresponding to state q and the column corresponds to input a is the state δ(q, a). 55 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 56. Transition Diagram • Transition graph can be interpreted as a flowchart for an algorithm recognizing a language. • A transition graph consists of three things: • A finite set of states, at least one of which is designated the start state and some of which are designated as final states. • An alphabet Σ of possible input symbols from which the input strings are formed. • A finite set of transitions that show the change of state from the given state on a given input. 56 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 57. Example DFA 57 states A b q0 q1 q2 q1 q1 q3 q2 q2 q3 *q3 q3 q3 A=({q0,q1,q2,q3},{a,b}δ,q0,{q3}) δ is given by δ(q0,a)=q1 δ(q0,b)=q2 δ(q1,a)=q1 δ(q2,b)=q2 δ(q1,b)=q3 δ(q2,a)=q3 δ(q3,a)=q3 δ(q3,b)=q3 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 58. • Design a DFA with ∑ = {0, 1} accepts those string which starts with 1 and ends with 0. • Design a DFA with ∑ = {0, 1} accepts the only input 101. 58 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 59. • Design a DFA with ∑ = {0, 1} accepts the strings with an even number of 0's end by single 1. 59 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 60. Extended transition function δ • The DFA define a language: the set of all strings that result in a sequence of state transitions from the start state to an accepting state • Extended Transition Function • Describes what happens when we start in any state and follow any sequence of inputs • If δ is our transition function, then the extended transition function is denoted by δ • The extended transition function is a function that takes a state q and a string w and returns a state p (the state that the automaton reaches when starting in state q and processing the sequence of inputs w) • Let w=va then δ(q, va) = δ(δ (q, v), a). 60 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 61. Language accepted by DFA • The language of a DFA A = (Q, Σ, δ, q0, F), denoted L(A) is defined by L(A) = { w | δ(q0, w) is in F } • The language of A is the set of strings w that take the start state q0 to one of the accepting states • If L is a L(A) from some DFA, then L is a regular language 61 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 62. Nondeterministic Finite Automata • An NFA is like a DFA, except that it can be in several states at once. • This can be seen as the ability to guess something about the input. • Useful for searching texts 62 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 63. Formal Definition of NFA • A nondeterministic finite automaton (NFA) is a 5-tuple (Q,Σ,δ,q0,F),where • Q is a finite set called the states, • Σ is a finite set called the alphabet, • δ:Q×Σ→P(Q) is the transition function, • q0 ∈ Q is the start state, and • F ⊆ Q is the set of accepting states. 63 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 64. Extended transition function δ • The extended transition function is a function that takes a state q and a string w and returns a set of states P (The set of possible state that the automaton reaches when starting in state q and processing the sequence of inputs w) • Let w=va then δ 𝑞0, 𝑣𝑎 = 𝑞′∈ δ 𝑞0,𝑣 δ( 𝑞′,a) 64 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 65. Language accepted by NFA • The language L(A) accepted by the NFA A is defined as follows: L(A) = {w | δ(q0, w) ∩ F ≠ ∅} 65 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 67. • Design an NFA with ∑ = {0, 1} in which double '1' is followed by double '0'. • Design an NFA with ∑ = {0, 1} accepts all string in which the third symbol from the right end is always 0. 67 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 68. Epsilon Nondeterministic Finite Automata • Formal Definition A ε-NFA is a quintuple A=(Q,Σ,δ,q0,F) where • Q is a set of states • Σ is the alphabet of input symbols • ε is never a member of Σ. Σε is defined to be (Σ ∪ ε) • δ: Q × Σε → P(Q) is the transition function • q0 ∈ Q is the initial state • F ⊆ Q is the set of final states 68 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 69. Example ε-NFA ε-NFA for a language which contain Os followed by 0 or more 1s. 69 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 70. ε- closure • Epsilon means present state can goto other state without any input. This can happen only if the present state have epsilon transition to other state. • Epsilon closure is finding all the states which can be reached from the present state on one or more epsilon transitions. ε- closure (0)={0,1,2} ε- closure(1)={1,2} ε- closure(2)={2} 70 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
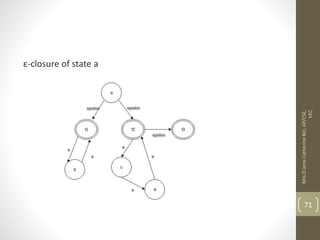
- 71. ε-closure of state a 71 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 72. ε-closure of state 0,1,2,3,4 72 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 74. δ - ε-NFA δ 𝑞0, 𝑣𝑎 = 𝑖=1 𝑘 δ(𝑝𝑖, 𝑎) = 𝑗=1 𝑚 𝐸𝑐𝑙𝑜𝑠𝑒(rj) Where δ (q0,v)= {p1,p2,…,pk } & 𝑖=1 𝑘 δ(𝑝𝑖, 𝑎)= {r1,r2,…,rm } 74 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 75. Language accepted by ε-NFA The language of an ε-NFA E = (Q, Σ, δ, q0, F) is L(E) = {w | ˆ δ(q0, w) ∩ F ≠ ∅} 75 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 77. • Every DFA is NFA but not vice versa. • Both NFA and DFA have same power and each NFA can be translated into a DFA. • There can be multiple final states in both DFA and NFA. • NFA is more of a theoretical concept. • DFA is used in Lexical Analysis in Compiler. • Every NFA is ε-NFA but not vice-versa 77 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 78. Conversion of NFA to DFA • Subset Construction Method 1. Create state table from the given NFA. 2. Create a blank state table under possible input alphabets for the equivalent DFA. 3. Mark the start state of the DFA by q0 (Same as the NFA). 4. Find out the combination of States {Q0, Q1,... , Qn} for each possible input alphabet. 5. Each time we generate a new DFA state under the input alphabet columns, we have to apply step 4 again, otherwise go to step 6. 6. The states which contain any of the final states of the NFA are the final states of the equivalent DFA. 78 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 81. Transition Diagram for the subset 81 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 83. NFA DFA State 0 1 →q0 q0 q1 q1 {q1, q2} q1 *q2 q2 {q1, q2} 83 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 84. Now we will obtain δ' transition for state q0. δ'([q0], 0) = [q0] δ'([q0], 1) = [q1] The δ' transition for state q1 is obtained as: δ'([q1], 0) = [q1, q2] (new state generated) δ'([q1], 1) = [q1] 84 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 85. Now we will obtain δ' transition on [q1, q2]. δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0) = {q1, q2} ∪ {q2} = [q1, q2] δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1) = {q1} ∪ {q1, q2} = {q1, q2} = [q1, q2] The state [q1, q2] is the final state as well because it contains a final state q2. 85 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 86. State 0 1 →[q0] [q0] [q1] [q1] [q1, q2] [q1] *[q1, q2] [q1, q2] [q1, q2] The transition table for the constructed DFA will be: 86 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 87. Conversion of ε-NFA to DFA • Modified subset construction 1. Find the ε-closure for the starting state of ε - NFA as a starting state of DFA. 2. Find the states for each input symbol that can be traversed from the present. That means the union of transition value and their closures for each state of NFA present in the current state of DFA. 3. If a new state is found, take it as current state and repeat step 2. 4. Repeat Step 2 and Step 3 until there is no new state present in the transition table of DFA. 5. Mark the states of DFA as a final state which contains the final state of ε-NFA. 87 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 88. Example • Let us obtain ε-closure of each state. ε-closure {q0} = {q0, q1, q2} ε-closure {q1} = {q1} ε-closure {q2} = {q2} ε-closure {q3} = {q3} ε-closure {q4} = {q4} 88 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 89. • let ε-closure {q0} = {q0, q1, q2} be state A δ'(A, 0) = ε-closure {δ((q0, q1, q2), 0) } = ε-closure {δ(q0, 0) ∪ δ(q1, 0) ∪ δ(q2, 0) } = ε-closure {q3} = {q3} call it as state B. δ'(A, 1) = ε-closure {δ((q0, q1, q2), 1) } = ε-closure {δ((q0, 1) ∪ δ(q1, 1) ∪ δ(q2, 1)} = ε-closure {q3} = {q3} = B. 89 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 90. δ'(B, 0) = ε-closure {δ(q3, 0) } = ϕ δ'(B, 1) = ε-closure {δ(q3, 1) } = ε-closure {q4} = {q4} i.e. state C δ'(C, 0) = ε-closure {δ(q4, 0) } = ϕ δ'(C, 1) = ε-closure {δ(q4, 1) } = ϕ 90 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 91. ε-closure(q0) = {q0, q1, q2} ε-closure(q1) = {q1, q2} ε-closure(q2) = {q2} 91 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 92. δ'(A, 0) = ε-closure{δ((q0, q1, q2), 0)} = ε-closure{δ(q0, 0) ∪ δ(q1, 0) ∪ δ(q2, 0)} = ε-closure{q0} = {q0, q1, q2} δ'(A, 1) = ε-closure{δ((q0, q1, q2), 1)} = ε-closure{δ(q0, 1) ∪ δ(q1, 1) ∪ δ(q2, 1)} = ε-closure{q1} = {q1, q2} call it as state B δ'(A, 2) = ε-closure{δ((q0, q1, q2), 2)} = ε-closure{δ(q0, 2) ∪ δ(q1, 2) ∪ δ(q2, 2)} = ε-closure{q2} = {q2} call it state C 92 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 93. δ'(B, 0) = ε-closure{δ((q1, q2), 0)} = ε-closure{δ(q1, 0) ∪ δ(q2, 0)} = ε-closure{ϕ} = ϕ δ'(B, 1) = ε-closure{δ((q1, q2), 1)} = ε-closure{δ(q1, 1) ∪ δ(q2, 1)} = ε-closure{q1} = {q1, q2} i.e. state B itself δ'(B, 2) = ε-closure{δ((q1, q2), 2)} = ε-closure{δ(q1, 2) ∪ δ(q2, 2)} = ε-closure{q2} = {q2} i.e. state C itself 93 Mrs.D.Jena Catherine Bel, AP/CSE, VEC
- 94. δ'(C, 0) = ε-closure{δ(q2, 0)} = ε-closure{ϕ} = ϕ δ'(C, 1) = ε-closure{δ(q2, 1)} = ε-closure{ϕ} = ϕ δ'(C, 2) = ε-closure{δ(q2, 2)} = {q2} 94 Mrs.D.Jena Catherine Bel, AP/CSE, VEC