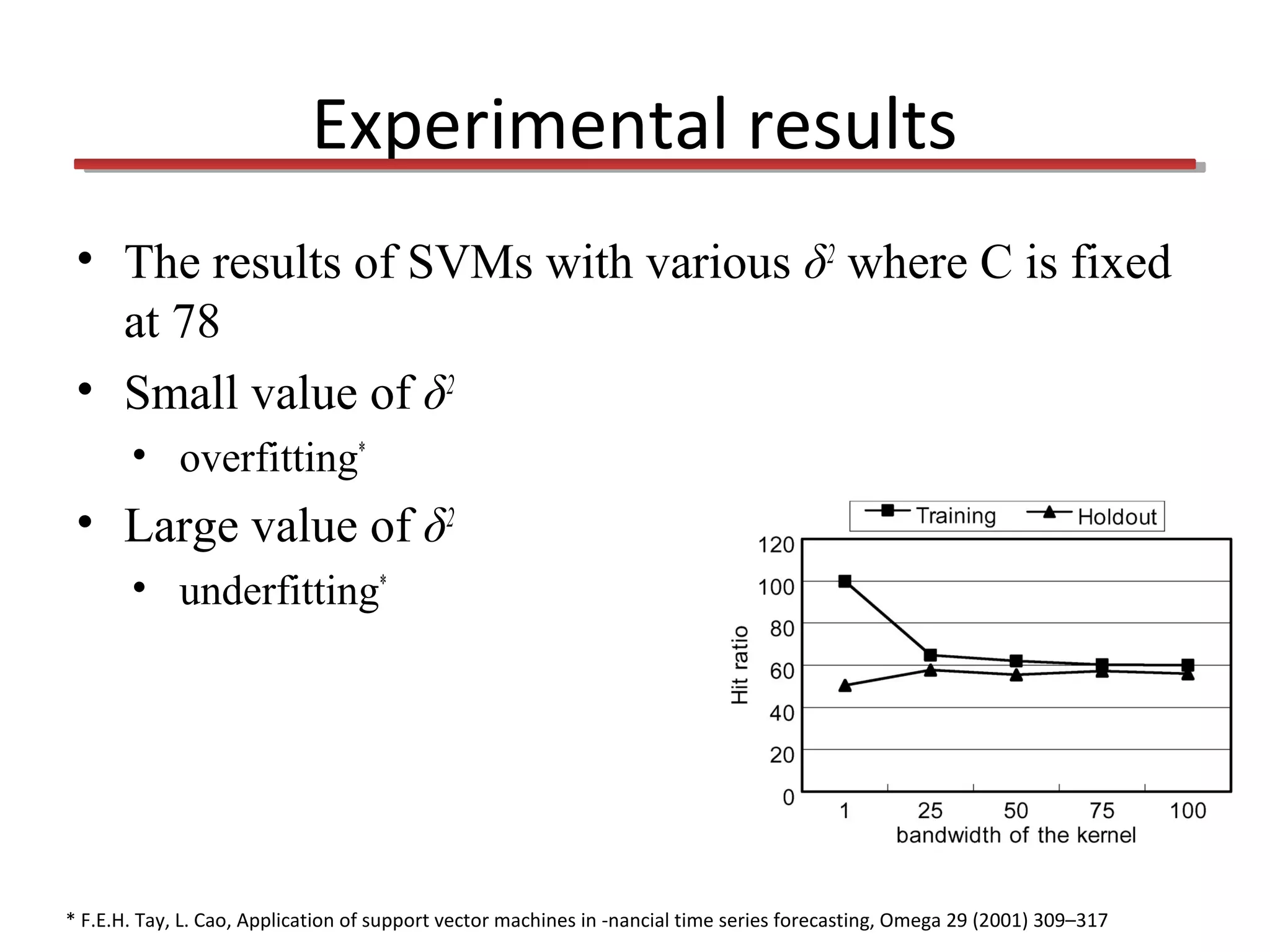
This document discusses using support vector machines (SVMs) for financial time series forecasting. It introduces SVMs and describes how they find the optimal separating hyperplane between classes of data. The document outlines experimental settings using SVMs, backpropagation networks, and case-based reasoning on stock market data. The results show SVMs outperform the other methods due to minimizing structural risk, but note issues with parameter tuning.