[한글] Tutorial: Sparse variational dropout
- 1. Tutorial: Sparse Variational Dropout Wu Hyun Shin MLAI, KAIST 7. 24. 2019.
- 2. 진행방식 • 실제 Variational Dropout을 위한 코드 구현은 간단 • 다른 수업에서 했던 모델링 + Dropout layer • BNN 학습을 위한 전체적 코드 구조는 두번째 시간과 유사 • 왜 이렇게 하고, 어떻게 해야하는지 원리를 이해하는 것이 더 중요 • 수학적 이해 및 공식 유도가 다소 요구됨 • 실제 주요 공식은 코드 한 줄로 구현 • 수업목표 • 수학적 디테일을 모두 이해하지 못하더라도, 논리적 흐름을 파악하는 것이 목표 • 이론 수업에서 보다는 더 자세한 이해 • 코드를 보고 실제 어떻게 구현되는지 이해
- 3. 읽어야 할 논문? Binary Dropout (BD) • Improving neural networks by preventing co-adaptation of feature detectors. Hinton et al. arXiv:1207.0508. 2012. 4002 • Dropout: a simple way to prevent neural networks from overfitting. Srivastava et al. JMLR 2014. 13126 Gaussian Dropout (GD) • Fast dropout training. Wang et al. ICML 2013. 249 Variational Dropout (VD) • Variational Dropout and the Local Reparameterization Trick. Kingma et al. NIPS 2015. 326 Sparse Variational Dropout (Sparse VD) ← Final goal! • Variational Dropout Sparsifies Deep Neural Networks. Molchanov et al. ICML 2017. 148 → 해당 논문들의 내용에서 차례차례 building block을 확보 → 그 building block들을 조립하여 최종 논문 이해
- 4. Big Picture Binary dropout Gaussian dropout Variational dropout Bayesian NN / Variational Inference Sparse Variational dropout
- 5. Big Picture Binary dropout Gaussian dropout Variational dropout Bayesian NN / Variational Inference Sparse Variational dropout
- 6. • Multiplicative Bernoulli Noise • ℎ𝑖 𝑛𝑒𝑤 = ℎ𝑖 𝑜𝑙𝑑 ∗ 𝒓 𝒃 • BD를 GD로 일반화 • 우리가 잘 알고 있는 그 dropout • p의 확률로 retain • 1-p의 확률로 drop • 반대로 표기하기도 함 𝑝(𝒓 𝒃) • Binary Dropout?
- 7. BD를 GD로 일반화 • 두 가지 상황, 같은 효과 • PyTorch에서는 두번째 케이스로 구현되어 있음. • Test time에 특별한 조치가 없다 는 점에서 더 편리 • 앞으로 두번째 케이스를 전제! 1 𝑝 𝑤 w𝑤 if 𝑘 = 1/𝑝, • 학습과 테스트 시의 차이
- 8. BD를 GD로 일반화 1 𝑝 𝑤 w𝑤 • 두번째 케이스를 살펴보자. • Bernoulli random variable 𝑟𝑏 • 평균? 𝒙𝒑(𝒙) • 𝐸 𝑟𝑏 = 1 𝑝 ∙ Pr 𝑟𝑏 = 1 𝑝 + 0 ∙ Pr 𝑟𝑏 = 0 = 1 𝑝 ∙ 𝑝 + 0 ∙ 1 − 𝑝 = 𝟏 • 분산? 𝑬 𝒓 𝒃 𝟐 − 𝑬 𝒓 𝒃 𝟐 • 𝐸 𝑟𝑏 2 = 1 𝑝 2 ∙ 𝑝 + 02 ∙ 1 − 𝑝 = 1 𝑝 • 𝑉𝑎𝑟 𝑟𝑏 = 𝐸 𝑟𝑏 2 − 𝐸 𝑟𝑏 2 = 1 𝑝 − 12 = 𝟏−𝒑 𝒑
- 9. BD를 GD로 일반화 • 같은 평균과 분산을 같는 Gaussian random variable 𝑟𝑔은? • 𝜇 = 1, 𝜎 = 1−𝑝 𝑝 • 𝑟𝑔~N 𝜇, 𝜎2 = 𝑁 𝟏, 𝟏−𝒑 𝒑 • 새로운 파라미터 𝛼 = 1−𝑝 𝑝 를 도입 • 𝑁 1, 𝛼 ← 앞으로 계속 보게 될 형태! ≈ • Multiplicative Gaussian Noise • ℎ𝑖 𝑛𝑒𝑤 = ℎ𝑖 𝑜𝑙𝑑 ∗ 𝑟𝑔 • 𝑟𝑔~𝑁 1, 𝛼 (𝛼 = 1−𝑝 𝑝 )
- 10. Big Picture Binary dropout Gaussian dropout Variational dropout Bayesian NN / Variational Inference Sparse Variational dropout
- 11. Recap: Bayesian Neural Networks • BNN이란? • Weight의 분포를 학습하는 네트워크 • 어떻게? • Bayes’ theorem을 이용 • , 𝑃𝑜𝑠𝑡𝑒𝑟𝑖𝑜𝑟 = 𝐿𝑖𝑘𝑒𝑙𝑖ℎ𝑜𝑜𝑑 ∗𝑃𝑟𝑖𝑜𝑟 𝐸𝑣𝑖𝑑𝑒𝑛𝑐𝑒 • 그런데 문제가 있다. • 분모를 계산할 수 없음. • 해결방법? • 직접 구할 수 없다면 근사하자. • 우리가 쓸 방법: Variational Inference
- 12. Recap: Variational Inference • Variational Inference란? • 우리의 posterior 𝑝(𝜃|𝐷)를 근사하는 기법 • 어떻게? • 우리가 쉽게 알 수 있는 분포를 설정하고: 𝑞 𝜙(𝜃) • 이 분포를 𝑝(𝜃|𝐷)와 가깝게 만들자! • 가까움의 기준? • KL Divergence • 우리가 풀어야할 문제? • 두 분포의 거리를 줄이는 문제 • 𝑞 𝜙 𝜃 = argmin 𝜙 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝 𝜃 𝐷 ] • Inference → optimization problem Variational distribution Variational parameter Posterior distribution
- 13. Recap: Variational Inference • 유도를 해보면? • 𝐾𝐿[𝑞 𝜙(𝜃)| 𝑝 𝜃 𝐷 + 𝐿 ? = log𝑝(𝐷) • 이제 𝐿 ? 를 maximize하면 되는 문제로 치환! • 𝐿 ? 의 실체? • 𝐿 ? = 𝑞 𝜙 𝜃 log𝑝 𝐷 𝜃 𝑑𝜃 − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)] • 직관적 해석: Expected Log-likelihood + KL regularization • ELBO(Evidence lower bound)라고 불림. • 왜? log𝑝 D ≥ 𝐿 ? • 결론: ELBO를 maximize하자! 상수
- 14. Recap: Variational Inference • 그래서 어떻게 구현? • 상황을 가정해보자. • 일반적인 classification 태스크 / FC네트워크 & single 레이어 • Weight가 Gaussian 𝑁(0, 𝐼)를 따를 것이 라는 사전(prior) 믿음 • 자연스럽게 weight의 사후 확률도 Gaussian으로 모델링 • 데이터에 대한 적절한 사후(posterior) 확률을 학습 • Weight 학습의 기대효과? • 우리의 사전 믿음을 기반으로 하되, (min KL term) • 데이터를 잘 표현하는 적절한 사후 확률분포를 학습 (min NLL term)
- 15. Recap: Variational Inference 𝜃 𝑋 𝑌∙ =B I O O B • 우리가 원하는 posterior 𝒒 𝝓 𝜽 : • 𝜃가 Gaussian에서 샘플링: 𝜃~N 𝜇, 𝜎2 • 미분 가능 (back-propagation 위해) • 그래서 어떻게 구현? Learnable parameter
- 16. Recap: Variational Inference 𝜃 𝑋 𝑌∙ =B I O O B 𝜇 𝑋 𝑌∙ =B I O O B 𝜎 𝜖⊙ + • 우리가 원하는 posterior 𝒒 𝝓 𝜽 : • 𝜃가 Gaussian에서 샘플링: 𝜃~N 𝜇, 𝜎2 • 미분 가능 (back-propagation 위해) • 그래서 어떻게 구현? • Reparametrization Trick(RT) • 𝜃 ∼ q 𝜙 𝜃 = N 𝜇, 𝜎2 → 𝜃 = 𝑓 𝜙, 𝜖 , 𝜖 ∼ 𝑝(𝜖) → 𝜃 = 𝜇 + 𝜎⊙ϵ , 𝜖~ 0, 𝐼
- 17. Recap: Variational Inference 𝜇 𝑋 𝑌∙ =B I O O B 𝜎 𝜖⊙ + • 그래서 어떻게 구현? • 이렇게 모델링한 뒤, • ELBO에 대하여 기존에 하던 것과 동일하게 minibatch-based training하면 끝! • 𝜙 = {𝜇, 𝜎} 일 때, • argmax 𝜙 𝑞 𝜙 𝜃 log𝑝 𝐷 𝜃 𝑑𝜃 − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)] • ≈ argmax 𝜙 𝑁 𝑀 𝑖=1 𝑀 log𝑝 𝑦 𝑖 𝑥 𝑖 , 𝑓(𝜙, 𝜖 𝑖 ) − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)] • 지금까지 한 것: • 미분가능한 파이프라인을 만듦(RT)으로써 minibatch 기반 학습을 가능케 함. • 이러한 방법을 Stochastic Gradient Variational Bayes(SGVB)라고 함. 보통 Analytic하게 계산Minibatch-based MC approximation 𝑁(0, 𝐼)
- 18. Recap: Variational Inference 𝜇 𝑋 𝑌∙ =B I O O B 𝜎 𝜖⊙ + • 그래서 어떻게 구현? • argmax 𝜙 𝑁 𝑀 𝑖=1 𝑀 log𝑝 𝑦 𝑖 𝑥 𝑖 , 𝑓(𝜙, 𝜖 𝑖 ) − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)] • 해석해보면? • 첫번째 항: 기존 Non-Bayesian과 똑같은 분류 성능 최적화 • 단, weight에 randomness가 추가된 상황 • 두번째 항: prior 𝑁(0, 𝐼)와의 KL divergence. • 우리의 초기 믿음에서 너무 벗어나지 않도록 regularize.
- 19. Recap: Variational Inference • 마지막으로 생각해볼 것들 • argmax 𝜙 𝑞 𝜙 𝜃 log𝑝 𝐷 𝜃 𝑑𝜃 − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)] • SGVB에서의 Gradient variance? • randomness가 개입되므로 gradient의 variance가 크다! • Source: data distribution p(𝐷) / noise distribution p 𝜖 • Variance를 줄이는 것은 학습 안정화에 매우 중요한 요소 • 두번째 항(KL term)은 가능한 경우, closed-form으로 직접 계산. • 계산 가능한데 근사할 필요는 없음 • 불필요한 gradient variance가 더 증가
- 20. Big Picture Binary dropout Gaussian dropout Variational dropout Bayesian NN / Variational Inference Sparse Variational dropout
- 21. VD: Variational Dropout • 전체 개요 • SGVB를 효율적으로 개선하려는 테크닉을 제안 • Local Reparametrization Trick(LRT) • Gradient variance를 낮추고 더 쉽고 빠르게 계산 • Dropout과 variational method의 연결점을 탐색 • GD + Varaitional method + LRT = Variational Dropout • 이를 통해 얻을 수 있는 것? • 발전 : GD의 성능 향상 (with LRT) • 확장 : 학습 가능한 dropout rate. • 재해석 : GD를 Bayesian network로 보았을 때 prior는 무엇일까? ← Part 1 ← Part 2
- 22. VD-Part 1: Local Reparameterization Trick • Local Reparameterization Trick(LRT)에 대해 알아보자. • 목적? SGVB를 효율적으로 개선 • SGVB의 gradient variance를 줄이자! • 먼저 해야할 일? Gradient variance의 요인을 분석 • 수학적 decomposition을 통해 분석
- 23. VD-Part 1: Local Reparameterization Trick • SGVB를 다시 살펴보자. • ELBO: (𝑥,𝑦∈𝐷) 𝐸 𝑞 𝜙 𝜃 [log𝑝(𝑦|𝑥, 𝜃)] − 𝐾𝐿[𝑞 𝜙 𝜃 ||𝑝 𝜃 ] • 두번째 KL term은 closed-form으로 계산이 가능하다고 가정. • Minibatch approximation: • (𝑥,𝑦∈𝐷) 𝐸 𝑞 𝜙 𝜃 [log𝑝(𝑦|𝑥, 𝜃)] ≈ 𝑁 𝑀 𝑖=1 𝑀 𝐥𝐨𝐠𝒑 𝒚𝒊 𝒙𝒊, 𝒇(𝝓, 𝝐𝒊) • 즉, SGVB는 𝑁 𝑀 𝑖=1 𝑀 𝑳𝒊의 꼴로 나타낼 수 있음. • 𝑳𝒊는 𝒊 번째 데이터에 대한 likelihood를 나타냄을 기억하자. 𝑞 𝜙 𝜃 log𝑝 𝐷 𝜃 𝑑𝜃 𝑀 : Minibatch size 𝑁: Data size
- 24. VD-Part 1: Local Reparameterization Trick • 그렇다면 𝑁 𝑀 𝑖=1 𝑀 𝐿𝑖의 variance는? • 𝑉𝑎𝑟 𝑁 𝑀 𝑖=1 𝑀 𝐿𝑖 • 알 수 있는 사실? • Variance의 영향은 minibatch size 𝑀을 키워서 줄일 수 있음. • 반면, Covariance의 경우는 불가능! • 우리가 원하는 것? • Cov 𝐿𝑖, 𝐿𝑗 = 0 • In Korean: Minibatch 안의 데이터들의 log-likelihood를 종속성을 제거
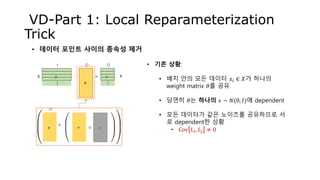
- 25. VD-Part 1: Local Reparameterization Trick • 데이터 포인트 사이의 종속성 제거 𝜃 𝑋 𝑌∙ =B I O O B 𝜇 O 𝜎 𝜖⊙ + • 기존 상황: • 배치 안의 모든 데이터 𝑥𝑖 ∈ 𝑋가 하나의 weight matrix 𝜃를 공유 • 당연히 𝜃는 하나의 𝜖 ∼ 𝑁(0, 𝐼)에 dependent • 모든 데이터가 같은 노이즈를 공유하므로 서 로 dependent한 상황 • Cov 𝐿𝑖, 𝐿𝑗 ≠ 0 … …
- 26. 𝑋 VD-Part 1: Local Reparameterization Trick • 데이터 포인트 사이의 종속성 제거 𝑌∙ =B I O O B 𝜃 𝜃 𝜃 𝜃 𝜇 O 𝜎 ⊙ + • 해결 방법? • 배치 안의 모든 데이터 𝑥𝑖 ∈ 𝑋가 각기 다른 weight matrix 𝜃𝑖를 공유 • 𝜃𝑖는 각기 다른 𝜖𝑖 ∼ 𝑁(0, 𝐼)에 dependent • 데이터 사이의 dependency가 제거됨 • 𝐶𝑜𝑣 𝐿𝑖, 𝐿𝑗 = 0 • 문제점? • 계산 비용 증가 (샘플링은 비싼 편) • 병렬화가 불가능 𝜖 𝜖 𝜖 𝜖 … …
- 27. 𝑊 𝑊 𝑊 𝐴 VD-Part 1: Local Reparameterization Trick • 데이터 포인트 사이의 종속성 제거 𝑊 𝐵∙ =𝑚 𝑖 𝑗 𝑗 𝑚 𝜇 O 𝜎 ⊙ + • 더 나은 방법? • 𝑤𝑖,𝑗가 Gaussian이면, 𝑏 𝑚,𝑗도 Gaussian. • If X,Y independent and normally distributed, X+Y is also normally distributed. 𝑎 𝑚,𝑖 𝑤 𝑚,𝑖 𝑏 𝑚,𝑗 *논문 표기로 통일 (X𝜃 = 𝑌 → 𝐴𝑊 = 𝐵) 𝜖 𝜖 𝜖 𝜖
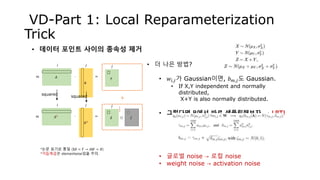
- 28. 𝛿 𝐴 VD-Part 1: Local Reparameterization Trick • 데이터 포인트 사이의 종속성 제거 𝜇 𝛾∙ =𝑚 𝑖 𝑗 𝑗 • 더 나은 방법? • 𝑤𝑖,𝑗가 Gaussian이면, 𝑏 𝑚,𝑗도 Gaussian. • If X,Y independent and normally distributed, X+Y is also normally distributed. • 그렇다면 B에서 바로 샘플링해보자. → LRT! • 글로벌 noise → 로컬 noise • weight noise → activation noise 𝐴2 𝜎2 ∙ =𝑚 𝑖 𝑗 𝑗 *논문 표기로 통일 (X𝜃 = 𝑌 → 𝐴𝑊 = 𝐵) *거듭제곱은 elementwise임을 주의. squared 𝜁⊙ + = 𝐵 1 2
- 29. 𝐴 VD-Part 1: Local Reparameterization Trick • 데이터 포인트 사이의 종속성 제거 𝜃 𝛾∙ =𝑚 𝑖 𝑗 𝑗 • 더 나은 방법? • 𝑤𝑖,𝑗가 Gaussian이면, 𝑏 𝑚,𝑗도 Gaussian. • If X,Y independent and normally distributed, X+Y is also normally distributed. • 그렇다면 B에서 바로 샘플링해보자. → LRT! • 글로벌 noise → 로컬 noise • weight noise → activation noise 𝐴2 𝜃2 ∙ =𝑚 𝑖 𝑗 *논문 표기로 통일 (X𝜃 = 𝑌 → 𝐴𝑊 = 𝐵) *거듭제곱은 elementwise임을 주의. squared +squared 𝛿 𝑗 𝜁⊙ 1 2
- 30. VD-Part 1: Local Reparameterization Trick • 𝐿𝑅𝑇의 장점? • 𝐿𝑖 서로 독립적 → Cov 𝐿𝑖, 𝐿𝑗 = 0 → 낮은 gradient variance! • 빠른 학습 (in terms of optimization step) • 더 작은 샘플링 횟수 & 병렬화 가능한 연산 • 빠른 학습 (in terms of wall-clock time) 𝜖 𝜖 𝜖 𝜖 𝜁 x 𝑚 Global noise Weight noise Local noise Activation/Units noise
- 31. VD-Part 2 • 지금까지.. • SGVB에서 사용 가능한 효율적인 테크닉: LRT • 이제부터.. • Dropout을 variational method로 재해석! • Varational dropout (with LRT)
- 32. VD-Part 2: Reinterpretation of GD as VD • Dropout과 variational method의 관계 Gaussian dropout • Multiplicative noise in units • 𝐵 = 𝐴⊙𝜉 𝜃, 𝜉 ∼ 𝑁 1, 𝛼 • LRT: • b 𝑚,𝑗 = 𝑖 𝑎 𝑚,𝑖 𝜉 𝑚,𝑖 𝜃𝑖,𝑗 • 𝐸 𝑏 𝑚,𝑗 = 𝑖 𝑎 𝑚,𝑖 𝜃𝑖,𝑗 𝐸 𝜉 𝑚,𝑖 = 𝑖 𝑎 𝑚,𝑖 𝜃𝑖,𝑗 • 𝑉𝑎𝑟 𝑏 𝑚,𝑗 = 𝑖 𝑎 𝑚,𝑖 2 𝜃𝑖,𝑗 2 𝑉𝑎𝑟 𝜉 𝑚,𝑖 = 𝛼 𝑖 𝑎 𝑚,𝑖 2 𝜃𝑖,𝑗 2 Variational Bayesian Inference • Noise in weights • 𝐵 = 𝐴W, W ∼ 𝑁 𝜃, 𝛼𝜃2 • LRT: • 𝑏 𝑚,𝑗 = 𝑖 𝑎 𝑚,𝑖 𝑤𝑖,𝑗 • 𝐸 𝑏 𝑚,𝑗 = 𝑖 𝑎 𝑚,𝑖 𝐸 𝑤𝑖,𝑗 = 𝑖 𝑎 𝑚,𝑖 𝜃𝑖,𝑗 • 𝑉𝑎𝑟 𝑏 𝑚,𝑗 = 𝑖 𝑎 𝑚,𝑖 2 𝑉𝑎𝑟 𝑤𝑖,𝑗 = 𝛼 𝑖 𝑎 𝑚,𝑖 2 𝜃𝑖,𝑗 2 재해석 *직접적 증명은 논문 appendix B 참 조. If then mean Multiplicative noise
- 33. VD-Part 2: Reinterpretation of GD as VD • Gaussian dropout과 Variational method의 유사성의 의미? • Variational Dropout을 제안! (드디어) • 이를 통해 얻을 수 있는 이점 • LRT를 이용해 Gaussian drop보다 안정적 학습 가능. • 이제 𝜶를 variational parameter로 놓고 학습할 수 있음. • min 𝜙 𝐾𝐿[𝑞 𝜙(𝑊)| 𝑝 𝑊 𝐷 에서 𝜙 = 𝜃, 𝛼 • 또다른 해석 가능: Prior는 뭘까? • Binary dropout ≈ Gaussian Dropout ≈ Variational Dropout • Binary dropout도 central limit theorem에 의해 근사 가능 • 참조: Fast dropout training. Wang et al. ICML 2013. mean Multiplicative noise
- 34. VD-Part 2: Reinterpretation of GD as VD • 그렇다면 prior는? • Gaussian dropout과의 consistency를 고려(꼭 필요한가?) • droprate 𝛼는 상수 / weight 𝜃에 대해서만 학습 𝜙 = 𝜃, 𝛼 • 𝐸𝐿𝐵𝑂에서 expected log-likelihood term에 대해서만 학습 • W ∼ 𝑁 𝜃, 𝛼 𝜃2 • max 𝜃 (𝑥,𝑦∈𝐷) 𝐸 𝑞 𝑊|𝜃,𝛼 [log𝑝(𝑦|𝑥, 𝑊)] − 𝐾𝐿[𝑞 𝑊|𝜃, 𝛼 ||𝑝 𝑊 ] • 이러한 조건을 만족하는 prior? • Log-uniform prior Has to be Independent to 𝜃(no effect), when 𝛼 is fixed.
- 35. VD-Part 2: Reinterpretation of GD as VD • Log-uniform distribution의 성질 log(𝑋) 𝑋 • Zero 근처에서 높은 density → weight에 적용할 경우 sparsity 유도 *MDL(Maximum Description Length) 관점으로 해석: weight를 floating point format으로 변환 시 log-uniform distribution을 따를 경우, 중요한 digit의 숫자를 최적으로 하여 압축 가능. weight의 크기를 제한하는 효과. (논문참조)
- 36. • Negative KL term을 closed-form으로 구할 수 있을까? • max 𝜙 (𝑥,𝑦∈𝐷) 𝐸 𝑞 𝜙 𝑊 [log𝑝(𝑦|𝑥, 𝑊)] − 𝐾𝐿[𝑞 𝜙 𝑊 ||𝑝 𝑊 ] • Appendix C를 믿는다면, • 결과적으로 항 때문에 계산 불가! • 그러나, 모든 𝛼에 대해 쉽게 샘플링 가능 VD-Part 2: Reinterpretation of GD as VD 𝜃에 independent Analytically intractable
- 37. VD-Part 2: Reinterpretation of GD as VD • 계산할 수 없다면 많이 샘플링해서 근사하자! • (1) 3차 다항식으로 근사: • (2) 더 간단한 lower bound: • ≥ 0 이므로, • 제한: 𝛼 ≤ 1 , 𝑝 ≤ 0.5 𝛼 = 1−𝑝 𝑝 • 이유? 𝛼가 클때, large gradient variance → local minima Intractable Approximated log𝛼 = 0 일 때, KL = 0 이 되도록 C 설정 → 완전히 drop (𝑝 = 1)불가능!
- 38. Big Picture Binary dropout Gaussian dropout Variational dropout Bayesian NN / Variational Inference Sparse Variational dropout
- 39. Sparse VD: • VD에서 무엇이 추가 되었나? • 기본전제: 𝛼에서 𝛼𝑖,𝑗로 확장 (weight별 독립적인 droprate 학습) • Additive Noise Reparameterization (1) • Gradient variance를 줄이기 위한 새로운 테크닉 • Approximation of the KL Divergence (2) • 𝛼의 범위에 제한(e.g. 𝛼 ≤ 1) 없이 학습 • 𝛼 → ∞ / 𝑝 → 1 : 항상 drop / 제거 가능 • 기타 등등 • 결과적으로? • 매우 sparse한 network 학습 • Bayesian pruning으로의 연결
- 40. Sparse VD: Additive Noise Reparametrization • VD에서의 문제점: • Droprate 𝜶가 큰 영역에서 𝜽에 대한 gradient variance가 매우 큼 • 해결방법: • 새로운 변수 도입 • 실제로는 𝛼대신에 𝐥𝐨𝐠 𝝈 𝟐를 학습 → 학습 안정 • 네트워크 output 자체를 𝐥𝐨𝐠 𝝈 𝟐값으로 해석 • 𝑤 = 𝜃 + exp 𝐥𝐨𝐠 𝝈 𝟐 ⋅ 𝜖 𝜃𝑖𝑗 + 𝜃𝑖𝑗 ∙ 𝛼𝑖𝑗 ∙ 𝜖𝑖𝑗 New variable 𝛼가 궁금하면 𝜃와의 관계에서 역으로 계산. 𝜎값 자체는 𝜃와 무관!
- 41. Sparse VD: Approximation of the KL term • KL term approximation: 모든 𝛂 영역에서 더 정확한 근사 • 사실상 Heuristic한 방법을 사용 • −0.5 log 1 + 𝛼−1 를 먼저 설정 • 남은 차이가 sigmoid와 비슷하다는 점에 착안하여 근사 함수 디자인 기존1: 0.5 log 𝛼 + 𝑐1 𝛼+c2 𝛼2+c3 𝛼3 기존2: 0.5 log 𝛼 새롭게 제안
- 42. Sparse VD: Sparsity • 𝛼 를 droprate 𝑝 관점에서 본다면? • 𝜶 → ∞ : 𝑝 → 1 이므로 항상 drop / 제거 가능 • 𝛼 를 w𝑖𝑗 에 더해지는 multiplicative noise관점에서 본다면? • 𝜶 → ∞ : 무한대의 noise / 완전한 random / 상쇄시켜야 함 𝜽𝒊𝒋 → 𝟎
- 43. Sparse VD: For convolution layers • Sparse VD for FC layers: 𝛼𝑖𝑗 𝜃𝑖𝑗 2 = 𝜎𝑖𝑗 2𝛿 𝑚𝑗 = 𝛼𝑖𝑗 𝑖=1 𝐼 𝑎 𝑚𝑖 2 𝜃𝑖𝑗 2 = 𝑖=1 𝐼 𝑎 𝑚𝑖 2 𝜎𝑖𝑗 2 By additive reparam. trick • Sparse VD for Conv layers:
- 44. Sparse VD: Empirical Observations • Test time에는? • 실제 완전히 드랍되는 경우는 없으므로 𝜶에 대한 thresholding이 필요 • Expected log likelihood term보다 KL term이 지배적인 경우가 더 일반적 • 초반에 급격하게 높은 sparsity로 수렴하여 학습에 실패 • 해결책? Pretraining or Scaling term 사용 • Prior 없이도 학습이 가능 • 사전 지식없이 데이터만 보고 variance를 fitting시킬 수 있음
- 45. Big Picture Binary dropout Gaussian dropout Variational dropout Bayesian NN / Variational Inference Sparse Variational dropout
- 46. Implementation 논문저자 공개 (Theano, Lasagne) • https://github.com/senya-ashukha/variational-dropout-sparsifies-dnn 다른 논문에서 활용 (TF / 저자 참여 / by Google AI research / 바로 사용하기 어려움) • https://github.com/google-research/google-research/tree/master/state_of_sparsity 개인 repository (TF / 미검증) • https://github.com/cjratcliff/variational-dropout (in progress) • https://github.com/BayesWatch/tf-variational-dropout (incomplete)
- 47. Any questions?











![Recap: Variational Inference
• Variational Inference란?
• 우리의 posterior 𝑝(𝜃|𝐷)를 근사하는 기법
• 어떻게?
• 우리가 쉽게 알 수 있는 분포를 설정하고: 𝑞 𝜙(𝜃)
• 이 분포를 𝑝(𝜃|𝐷)와 가깝게 만들자!
• 가까움의 기준?
• KL Divergence
• 우리가 풀어야할 문제?
• 두 분포의 거리를 줄이는 문제
• 𝑞 𝜙 𝜃 = argmin
𝜙
𝐾𝐿[𝑞 𝜙(𝜃)||𝑝 𝜃 𝐷 ]
• Inference → optimization problem
Variational distribution
Variational parameter
Posterior distribution](https://image.slidesharecdn.com/tutorialsparsevariationaldropout-190728122300/85/Tutorial-Sparse-variational-dropout-12-320.jpg)
![Recap: Variational Inference
• 유도를 해보면?
• 𝐾𝐿[𝑞 𝜙(𝜃)| 𝑝 𝜃 𝐷 + 𝐿 ? = log𝑝(𝐷)
• 이제 𝐿 ? 를 maximize하면 되는 문제로 치환!
• 𝐿 ? 의 실체?
• 𝐿 ? = 𝑞 𝜙 𝜃 log𝑝 𝐷 𝜃 𝑑𝜃 − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)]
• 직관적 해석: Expected Log-likelihood + KL regularization
• ELBO(Evidence lower bound)라고 불림.
• 왜? log𝑝 D ≥ 𝐿 ?
• 결론: ELBO를 maximize하자!
상수](https://image.slidesharecdn.com/tutorialsparsevariationaldropout-190728122300/85/Tutorial-Sparse-variational-dropout-13-320.jpg)



![Recap: Variational Inference
𝜇
𝑋 𝑌∙ =B
I O O
B
𝜎 𝜖⊙
+
• 그래서 어떻게 구현?
• 이렇게 모델링한 뒤,
• ELBO에 대하여 기존에 하던 것과 동일하게 minibatch-based training하면 끝!
• 𝜙 = {𝜇, 𝜎} 일 때,
• argmax
𝜙
𝑞 𝜙 𝜃 log𝑝 𝐷 𝜃 𝑑𝜃 − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)]
• ≈ argmax
𝜙
𝑁
𝑀 𝑖=1
𝑀
log𝑝 𝑦 𝑖
𝑥 𝑖
, 𝑓(𝜙, 𝜖 𝑖
) − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)]
• 지금까지 한 것:
• 미분가능한 파이프라인을 만듦(RT)으로써 minibatch 기반 학습을 가능케 함.
• 이러한 방법을 Stochastic Gradient Variational Bayes(SGVB)라고 함.
보통 Analytic하게 계산Minibatch-based
MC approximation
𝑁(0, 𝐼)](https://image.slidesharecdn.com/tutorialsparsevariationaldropout-190728122300/85/Tutorial-Sparse-variational-dropout-17-320.jpg)
![Recap: Variational Inference
𝜇
𝑋 𝑌∙ =B
I O O
B
𝜎 𝜖⊙
+
• 그래서 어떻게 구현?
• argmax
𝜙
𝑁
𝑀 𝑖=1
𝑀
log𝑝 𝑦 𝑖
𝑥 𝑖
, 𝑓(𝜙, 𝜖 𝑖
) − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)]
• 해석해보면?
• 첫번째 항: 기존 Non-Bayesian과 똑같은 분류 성능 최적화
• 단, weight에 randomness가 추가된 상황
• 두번째 항: prior 𝑁(0, 𝐼)와의 KL divergence.
• 우리의 초기 믿음에서 너무 벗어나지 않도록 regularize.](https://image.slidesharecdn.com/tutorialsparsevariationaldropout-190728122300/85/Tutorial-Sparse-variational-dropout-18-320.jpg)
![Recap: Variational Inference
• 마지막으로 생각해볼 것들
• argmax
𝜙
𝑞 𝜙 𝜃 log𝑝 𝐷 𝜃 𝑑𝜃 − 𝐾𝐿[𝑞 𝜙(𝜃)||𝑝(𝜃)]
• SGVB에서의 Gradient variance?
• randomness가 개입되므로 gradient의 variance가 크다!
• Source: data distribution p(𝐷) / noise distribution p 𝜖
• Variance를 줄이는 것은 학습 안정화에 매우 중요한 요소
• 두번째 항(KL term)은 가능한 경우, closed-form으로 직접 계산.
• 계산 가능한데 근사할 필요는 없음
• 불필요한 gradient variance가 더 증가](https://image.slidesharecdn.com/tutorialsparsevariationaldropout-190728122300/85/Tutorial-Sparse-variational-dropout-19-320.jpg)



![VD-Part 1: Local Reparameterization
Trick
• SGVB를 다시 살펴보자.
• ELBO: (𝑥,𝑦∈𝐷) 𝐸 𝑞 𝜙 𝜃
[log𝑝(𝑦|𝑥, 𝜃)] − 𝐾𝐿[𝑞 𝜙 𝜃 ||𝑝 𝜃 ]
• 두번째 KL term은 closed-form으로 계산이 가능하다고 가정.
• Minibatch approximation:
• (𝑥,𝑦∈𝐷) 𝐸 𝑞 𝜙 𝜃
[log𝑝(𝑦|𝑥, 𝜃)] ≈
𝑁
𝑀 𝑖=1
𝑀
𝐥𝐨𝐠𝒑 𝒚𝒊 𝒙𝒊, 𝒇(𝝓, 𝝐𝒊)
• 즉, SGVB는
𝑁
𝑀 𝑖=1
𝑀
𝑳𝒊의 꼴로 나타낼 수 있음.
• 𝑳𝒊는 𝒊 번째 데이터에 대한 likelihood를 나타냄을 기억하자.
𝑞 𝜙 𝜃 log𝑝 𝐷 𝜃 𝑑𝜃
𝑀 : Minibatch size
𝑁: Data size](https://image.slidesharecdn.com/tutorialsparsevariationaldropout-190728122300/85/Tutorial-Sparse-variational-dropout-23-320.jpg)








![VD-Part 2: Reinterpretation of GD as
VD
• 그렇다면 prior는?
• Gaussian dropout과의 consistency를 고려(꼭 필요한가?)
• droprate 𝛼는 상수 / weight 𝜃에 대해서만 학습 𝜙 = 𝜃, 𝛼
• 𝐸𝐿𝐵𝑂에서 expected log-likelihood term에 대해서만 학습
• W ∼ 𝑁 𝜃, 𝛼 𝜃2
• max
𝜃 (𝑥,𝑦∈𝐷) 𝐸 𝑞 𝑊|𝜃,𝛼
[log𝑝(𝑦|𝑥, 𝑊)] − 𝐾𝐿[𝑞 𝑊|𝜃, 𝛼 ||𝑝 𝑊 ]
• 이러한 조건을 만족하는 prior?
• Log-uniform prior
Has to be Independent to 𝜃(no
effect),
when 𝛼 is fixed.](https://image.slidesharecdn.com/tutorialsparsevariationaldropout-190728122300/85/Tutorial-Sparse-variational-dropout-34-320.jpg)

![• Negative KL term을 closed-form으로 구할 수 있을까?
• max
𝜙 (𝑥,𝑦∈𝐷) 𝐸 𝑞 𝜙 𝑊
[log𝑝(𝑦|𝑥, 𝑊)] − 𝐾𝐿[𝑞 𝜙 𝑊 ||𝑝 𝑊 ]
• Appendix C를 믿는다면,
• 결과적으로 항 때문에 계산 불가!
• 그러나, 모든 𝛼에 대해 쉽게 샘플링 가능
VD-Part 2: Reinterpretation of GD as
VD
𝜃에 independent
Analytically intractable](https://image.slidesharecdn.com/tutorialsparsevariationaldropout-190728122300/85/Tutorial-Sparse-variational-dropout-36-320.jpg)










