UNIT-4 TREES.ppt
- 1. DATA STRUCTURES AND ALGORITHMS ANALYSIS Trees M.Sivakumar, AP/AI&DS, KONGUNADU COLLEGE OF ENGINEERING AND TECHNOLOGY
- 2. Trees Introductions Tree is a non-linear data structure which organizes data in a hierarchical structure and this is a recursive definition. A tree is a connected graph without any circuits. If in a graph, there is one and only one path between every pair of vertices, then it is called tree. as a tree.
- 4. Tree Definition Tree is a non-linear data structure which organizes data in hierarchical structure and this is a recursive definition.
- 5. Tree terminology 1.Root: The first node is called as Root Node. Every tree must have root node, there must be only one root node. Root node doesn't have any parent.
- 6. 2. Edge In a tree data structure, the connecting link between any two nodes is called as EDGE. In a tree with 'N' number of nodes there will be a maximum of 'N-1' number of edges.
- 7. 3. Parent In a tree data structure, the node which is predecessor of any node is called as PARENT NODE. In simple words, the node which has branch from it to any other node is called as parent node. Parent node can also be defined as "The node which has child / children".
- 8. 4. Child The node which has a link from its parent node is called as child node. In a tree, any parent node can have any number of child nodes. In a tree, all the nodes except root are child nodes.
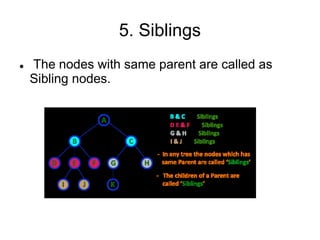
- 9. 5. Siblings The nodes with same parent are called as Sibling nodes.
- 10. 6. Leaf Node The node which does not have a child is called as LEAF Node. The leaf nodes are also called as External Nodes or 'Terminal' node.
- 11. 7. Internal Nodes An internal node is a node with atleast one child. Nodes other than leaf nodes are called as Internal Nodes. The root node is also said to be Internal Node if the tree has more than one node. Internal nodes are also called as 'Non- Terminal' nodes.
- 12. 8. Degree In a tree data structure, the total number of children of a node is called as DEGREE of that Node.
- 13. 9. Level In a tree data structure, the root node is said to be at Level 0 and the children of root node are at Level 1 and the children of the nodes which are at Level 1 will be at Level 2 and so on... In a tree each step from top to bottom is called as a Level and the Level count starts with '0' and incremented by one at each level (Step).
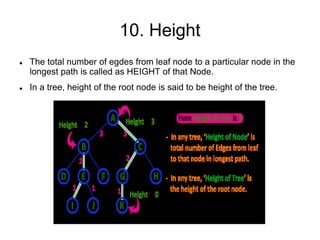
- 14. 10. Height The total number of egdes from leaf node to a particular node in the longest path is called as HEIGHT of that Node. In a tree, height of the root node is said to be height of the tree.
- 15. 11. Depth In a tree data structure, the total number of egdes from root node to a particular node is called as DEPTH of that Node.
- 16. 12. Path In a tree data structure, the sequence of Nodes and Edges from one node to another node is called as PATH between that two Nodes. Length of a Path is total number of nodes in that path. In below example the path A - B - E - J has length 4.
- 17. 13. Sub Tree Every child node will form a subtree on its parent node.
- 18. Type of Trees • General tree • Binary tree • Binary Search Tree
- 19. General Tree • A general tree is a data structure in that each node can have infinite number of children . • In general tree, root has in-degree 0 and maximum out-degree n. • Height of a general tree is the length of longest path from root to the leaf of tree. •
- 20. Binary tree • A Binary tree is a data structure in that each node has at most two nodes left and right • In binary tree, root has in-degree 0 and maximum out-degree 2. • In binary tree, each node have in-degree one and maximum out- degree 2. • Height of a binary tree is : Height(T) = { max (Height(Left Child) , Height(Right Child) + 1}
- 21. Representation of Binary Tree 1. Array Representation 2. Linked List Representation.
- 22. Representation of Binary Tree Struct node { int data; struct node * left,right; };
- 23. Array Representation 1. To represent a tree in one dimensional array nodes are marked sequentially from left to right start with root node. 2. First array location can be used to store no of nodes in a tree.
- 24. Linked Representation 1. This type of representation is more efficient as compared to array. 2. Left and right are pointer type fields left holds address of left child and right holds address of right child. 3. Struct node { int data; struct node * left,*right; };
- 25. Binary Tree Types 1. Extended Binary Tree 2. Complete Binary Tree 3. Full Binary Tree 4. Expression Binary tree
- 26. Extended Binary Tree An extended binary tree is a transformation of any binary tree into a completebinary tree. This transformation consists of replacing every null subtree of the original tree with “special nodes”or “failure nodes” .The nodes from the original tree are then internal nodes, while the “special nodes” are external nodes.
- 27. Complete Binary Tree A complete binary tree is a tree in which 1.All leaf nodes are at n or n-1 level 2.Levels are filled from left to right
- 28. Full Binary Tree A full binary tree (sometimes proper binary tree or 2-tree) is a tree in which every node other than the leaves has two children or no childeren. Every level is completely filled up. No of nodes= 2h+1 -1
- 29. Expression Binary tree • Expression trees are a special kind of binary tree used to evaluate certain expressions. • Two common types of expressions that a binary expression tree can represent are algebraic and boolean. • These trees can represent expressions that contain both unary and binary operators. • The leaves of a binary expression tree are operands, such as constants or variable names, and the other nodes contain operators. • Expression tree are used in most compilers.
- 31. Binary Tree Traversal 1. Preorder traversal:-In this traversal method first process root element, then left sub tree and then right sub tree. Procedure:- Step 1: Visit root node Step 2: Visit left sub tree in preorder Step 3: Visit right sub tree in preorder
- 32. 2. Inorder traversal:- In this traversal method first process left element, then root element and then the right element. Procedure:- Step 1: Visit left sub tree in inorder Step 2: Visit root node Step 3: Visit right sub tree in inorder
- 33. 3. Postorder traversal:- In this traversal first visit / process left sub tree, then right sub tree and then the root element. Procedure:- Step 1: Visit left sub tree in postorder Step 2: Visit right sub tree in postorder Step 3: Visit root node
- 34. Binary Search Tree A binary search tree (BST) or "ordered binary tree" is a empty or in which each node contains a key that satisfies following conditions: 1. All keys are distinct.’ 2. , all elements in its left subtree are less to the node (<), and all the elements in its right subtree are greater than the node (>).
- 35. Binary search tree Binary search tree property For every node X All the keys in its left subtree are smaller than the key value in X All the keys in its right subtree are larger than the key value in X
- 36. Binary Search Trees A binary search tree Not a binary search tree