Unit-I Recursion.pptx
- 1. Recursive thinking 1 Recursion is a problem-solving approach that can be used to generate simple solutions to certain kinds of problems that would be difficult to solve in other ways Recursion splits a problem into one or more simpler versions of itself ► These sub-problems may also be divided into further smaller sub-sub-problems Arecursive call is a function call in which the called function is the same as the one making the call
- 2. Recursive Definitions 2 Recursive algorithm ► Algorithm that finds the solution to a given problem by reducing the problem to smaller versions of itself ► Has one or more base cases ► Implemented using recursive functions Recursive function ► Function that calls itself
- 3. Recursive Definitions 3 Base case ► Case in recursive definition in which the solution is obtained directly ► Stops the recursion General case ► Case in recursive definition in which a smaller version of itself is called ► Must eventually be reduced to a base case
- 4. Outline of a recursive function 4 if (answer is known) provide the answer Base case else make a recursive call to Recursive case solve a smaller version of the same problem
- 5. Tracing a recursive function 5 Recursive function ► May have unlimited copies of itself ► Every recursive call has - its own code - own set of parameters - own set of local variables After completing recursive call ► Control goes back to calling environment ► Recursive call must execute completely before control goes back to previous call ► Execution in previous call begins from point immediately following recursive call
- 6. How Recursion Works? 6 Recursive function call is handled like any other function call Each recursive call has an activation record or a stack frame ► Stores values of parameters and local variables When base case is reached, return is made to previous call ► Recursion “unwinds”
- 7. Factorial definition 4! = 4 * 3 * 2 * 1 n! = n * (n-1) * … * 1 4! = 4 * 3! n! = n * (n-1)! factorial(n) = n * factorial(n-1) factorial(1) = 1 // recursive step // base step n! = 1 𝑛 ∗ 𝑛 − 1 ! 7 𝑖𝑓𝑛 = 0 𝑖𝑓 𝑛 > 0
- 8. Recursive factorial function 8 int fact(int num) { if(num == 0) return 1; else return num * fact(num – 1); }
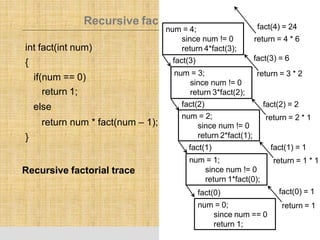
- 9. Recursive fac int fact(int num) { if(num == 0) return 1; else return num * fact(num – 1); } torial function num = 0; since num == 0 return 1; fact(0) fact(0) = 1 return = 1 num = 1; since num != 0 return 1*fact(0); fact(1) num = 2; since num != 0 return 2*fact(1); fact(2) num = 3; since num != 0 return 3*fact(2); fact(3) num = 4; since num != 0 return 4*fact(3); fact(1) = 1 return = 1 * 1 fact(2) = 2 return = 2 * 1 fact(3) = 6 return = 3 * 2 fact(4) = 24 return = 4 * 6 Recursive factorial trace
- 10. Another recursive definition Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, ... 0 𝑓𝑜𝑟 𝑛 == 0 𝑓𝑖𝑏 𝑛 = ൞1 𝑓𝑜𝑟 𝑛 == 1 𝑓𝑖𝑏 𝑛 − 2 + 𝑓𝑖𝑏 𝑛 − 1 𝑓𝑜𝑟 𝑛 > 2 fib(n) = fib(n-1) + fib(n-2) Recursive case fib(0) = 0 fib(1) = 1 Base case 10
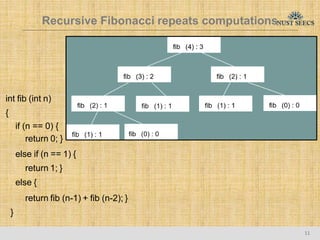
- 11. int fib (int n) { if (n == 0) { return 0; } else if (n == 1) { return 1; } else { return fib (n-1) + fib (n-2); } } Recursive Fibonacci repeats computations 11
- 12. Evaluating Exponents Recursively 12 double power (double x, unsigned int n) // raise x to the power n { if (n == 0) return 1.0; else return x * power(x,n-1); } Using this definition, the value of x4 can be computed in the following way: x4 = x · x3 = x · (x · x2 ) = x · (x · (x · x1 )) = x · (x · (x · (x · x0 ))) = x · (x · (x · (x · 1))) = x · (x · (x · (x))) = x · (x · (x · x)) = x · (x · x · x) = x · x · x · x
- 13. Implementation using loop 13 The function power() can also be implemented differently, without using any recursion, as in the following loop: double nonRecPower(double x, unsigned int n) { double result = 1; for (result = x; n > 1; --n) result *= x; return result; } Do we gain anything by using recursion instead of a loop?
- 14. Recursion or iteration? 14 The recursive version seems to be more intuitive because it is similar to the original definition of the power function. The definition is simply expressed in C++ without losing the original structure of the definition The recursive version increases program readability, improves self-documentation, and simplifies coding In the example, the code of the nonrecursive version is not substantially larger than in the recursive version, but for most recursive implementations, the code is shorter than it is in the non-recursive implementations
- 15. Recursive vs iteration 15 In iteration, a loop repetition condition determines whether to repeat the loop body or exit from the loop In recursion, the condition usually tests for a base case You can always write an iterative solution to a problem that is solvable by recursion Recursive code may be simpler than an iterative algorithm and thus easier to write, read, and debug
- 16. When to use recursion? 16 If recursive and iterative algorithms are of similar efficiency ► Prefer iteration over recursion If the problem is inherently recursive and a recursive algorithm is less complex to write than an iterative algorithm ► Prefer recursion over iteration
- 17. Efficiency of recursion 17 Recursive methods often have slower execution times when compared to their iterative counterparts ► Because the overhead for loop repetition is smaller than the overhead for a method call and return If it is easier to conceptualize an algorithm using recursion, then you should code it as a recursive method ► Because sometimes the reduction in efficiency does not outweigh the advantage of readable code that is easy to debug
- 18. Pitfalls of recursion 18 One pitfall of recursion is infinite regress, i.e. a chain of recursive calls that never stops ► E.g. if you forget the base case. Make sure you have enough base cases Recursion can be less efficient than an iterative implementation. This can happen because there is recalculation of intermediate results There can be extra memory use because recursive calls must be stored on the execution stack
- 19. Function calls & recursive implementation 19 The state of each function, including main(), is characterized ► by the contents of all local variables, ► by the values of the function’s parameters, and ► by the return address indicating where to restart in the calling function The data area containing all this information is called an activation record or a stack frame and is allocated on the run-time stack ► exists for as long as a function owning it is executing This record is a private pool of information for the function, a repository that stores all information necessary for its proper execution and how to return to where it was called from
- 20. Activation Record / Stack Frame If a function is called either by main() or by another function, then its stack frame is created on the run-time stack The run-time stack always reflects the current state of the function ► E.g., suppose that main() calls function f1(), f1() calls f2(), and f2() in turn calls f3(). If f3() is being executed, then the state of the run-time stack is as shown 20
- 21. Activation Record / Stack Frame 21 An activation record usually contains the following information ► Values for all parameters to the function, location of the first cell if an array is passed or a variable is passed by reference, and copies of all other data items; ► Local variables that can be stored elsewhere, in which case, the activation record contains only their descriptors and pointers to the locations where they are stored; ► The return address to resume control by the caller, the address of the caller’s instruction immediately following the call; ► A dynamic link, which is a pointer to the caller’s activation record; ► The returned value for a function not declared as void. Because the size of the activation record may vary from one call to another, the returned value is placed right above the activation record of the caller
- 22. Evaluating Exponents Recursively 22 double power (double x, unsigned int n) /* 102 */ { /* 103 */ /* 104 */ if (n == 0) return 1.0; else return x * power(x,n-1); } /* 105 */ int main() { ... y = power(5.6,2); ... } /* 136 */
- 23. double power (double x, unsigned int n) { /* 102 */ 23 /* 103 */ /* 104 */ if (n == 0) return 1.0; else return x * power(x,n-1); } /* 105 */ First, the value of the second argument, i.e., 2, is checked, and power() tries to return the value of 5.6 * power(5.6,1)
- 24. double power (double x, unsigned int n) { /* 102 */ /* 103 */ /* 104 */ if (n == 0) return 1.0; else return x * power(x,n-1); } /* 105 */ 24 Again first, the value of the second argument, i.e., 1, is checked, and power() tries to return the value of 5.6 * power(5.6,0)
- 25. double power (double x, unsigned int n) { /* 102 */ /* 103 */ /* 104 */ if (n == 0) return 1.0; else return x * power(x,n-1); } /* 105 */ 25
- 26. Again, first, the value of the second argument, i.e., 0, is checked, and power() returns the value 1 double power (double x, unsigned int n) { /* 102 */ /* 103 */ /* 104 */ if (n == 0) return 1.0; else return x * power(x,n-1); } /* 105 */ 26 At this point, there are two pending calls on the run-time stack—the calls to power()— that have to be completed
- 27. 5.6 * power(5.6,0) = 5.6 * 1 = 5.6 is computed double power (double x, unsigned int n) { /* 102 */ /* 103 */ /* 104 */ if (n == 0) return 1.0; else return x * power(x,n-1); } /* 105 */ 27
- 28. 5.6 * power(5.6,0) = 5.6 * 1 = 5.6 is computed double power (double x, unsigned int n) { /* 102 */ /* 103 */ /* 104 */ if (n == 0) return 1.0; else return x * power(x,n-1); } /* 105 */ 28
- 29. 5.6 * power(5.6,1) = 5.6 * 5.6 = 31.36 is computed double power (double x, unsigned int n) { /* 102 */ /* 103 */ /* 104 */ if (n == 0) return 1.0; else return x * power(x,n-1); } /* 105 */ 29
- 30. 5.6 * power(5.6,1) = 5.6 * 5.6 = 31.36 is computed double power (double x, unsigned int n) { /* 102 */ /* 103 */ /* 104 */ if (n == 0) return 1.0; else return x * power(x,n-1); } /* 105 */ 30