Mining event streams with BeepBeep 3
- 1. MINING event streams with Sylvain Hallé, Raphaël Khoury Massiva Roudjane, Eva Terzago Quen�n Be�, Paul Lesur
- 2. $$$$$ $$$$$ $$$$$ x=104 y=12 x=232 y=21 119.5 s 4 1-2 1955-11-12 APPL MSFT =123.34 =208.56 GOGL AMZN =314.16 =271.82 10432.3 Src Dst =1.2.3.4:403 =5.6.7.8:221 Many elements of so�ware systems can be modelled as pieces of data called events.
- 3. A stream (or trace) is a sequence of events. The rate at which events are produced is called the throughput. A stored copy of a stream is called a log. . . .
- 4. ” ∑ Event streams can be processed in various ways. Some examples: Aggrega�on Pa�ern detec�on Visualiza�on What is the average price of MSFT over 5 days? Display bandwidth usage for the last 24 hours. Does ever collide with ? ” ” “ “ “
- 5. We are interested in two special kinds of computa�on over streams. Compu�ng trends over a stream Finding out if a stream deviates from a given trend
- 6. We are interested in two special kinds of computa�on over streams. Compu�ng trends over a stream Finding out if a stream deviates from a given trend data mining monitoring
- 7. Event stream query engine developed based on the previous observations Aims at borrowing strengths from both RV and CEP (and beyond) Key concepts: composability, modularity, extensibility Open source, developed in Java http://liflab.github.io/beepbeep-3 peeB peeB 3
- 8. EventsEvents An event is an element e taken from some set E, called the event type. No restriction on the type! In BeepBeep, events can be any Object. Booleans Numbers 2 3 4 π Strings abc Functions Sets PlotsTuples 3 8 a 3 8 a 2 6 c + ⊇? XML documents <a><a><a> . . . ?
- 9. TracesTraces An event trace (or event stream) is a potentially infinite sequence of events of a given type: 2 0 6 3 4 9 . . . Traces are symbolically denoted by: e = e0 e1 e2 e3 ... The set of all traces of type T is denoted as: T*
- 10. FunctionsFunctions A function takes 0 or more events as its input, and returns 1 or more events. Functions are first-class objects; they descend from the class Function 1 : 1 function 2 : 1 function 1 : 2 function ⊇? 3 4 2+5i ₹ 2 5 6 0 : 1 function 6
- 11. ProcessorsProcessors A processor takes 0 or more event traces as its input, and returns 0 or more event traces as its output 1 : 1 processor 2 : 1 processor . . . . . .
- 12. ProcessorsProcessors When a processor takes more than one input trace, the set of events at matching positions in each trace is called a front. bacd 3601 b 3 a 6 c 0 d 1 1st event 2nd 3rd 4th . . . . . . . . .
- 13. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒
- 14. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 5 3
- 15. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 5 3
- 16. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 5 3 +
- 17. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 8
- 18. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 1
- 19. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 1
- 20. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 6 1
- 21. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 6 1
- 22. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 6 1 4
- 23. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 6 1 4
- 24. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 6 1 4 +
- 25. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 6 5
- 26. Synchronous processingSynchronous processing Events are processed one front at a time. + Buffers collect events until a complete front can be processed. ⇒ 6
- 27. Synchronous processingSynchronous processing Makes a couple of things simpler Don't care about what event arrived first or upstream computation time "Pen and paper" calculation is identical to the real one Otherwise, can do a lot with simple timeouts ⇒ contained asynchrony Motto: Don't use asychronous processing...
- 28. Synchronous processingSynchronous processing Makes a couple of things simpler Don't care about what event arrived first or upstream computation time "Pen and paper" calculation is identical to the real one Otherwise, can do a lot with simple timeouts ⇒ contained asynchrony Motto: Don't use asychronous processing... ...unless you really have to
- 29. Synchronous processingSynchronous processing In BeepBeep, all synchronous processors are descendents of the SingleProcessor class Takes care of handling input/output buffers Calls (abstract) method process() when an input front is ready to be consumed Processor only needs to produce an output front from this input Makes it easy to create your own (more on that later)
- 30. A high-level event trace can be produced by composing ("piping") together one or more processors from lower-level traces CompositionComposition
- 31. Each processor has its own input/output buffers CompositionComposition
- 32. Any output can be connected to any input, as long as they have the same type CompositionComposition
- 33. Any output can be connected to any input, as long as they have the same type CompositionComposition Many types can occur in the same chain
- 34. ArchitectureArchitecture BeepBeep provides only a few built-in processors and functions Palette Set of processors and functions, centered around a particular use case Concretely, a JAR library defining new Processor and Function objects
- 35. <? + <? =? − ÷ × f Σ f n { n n Function Cumulative Trim ForkDecimate Group WindowSliceFilter Built-in processors Built-in functions .n < <
- 36. SemanticsSemantics Let P be a processor and a b c = a1,a2,... = b1,b2,... = c1,c2,... be traces a,b,c : P[[ n = e1,e2,... denotes the n-th output trace of P, given traces a, b, c as input.
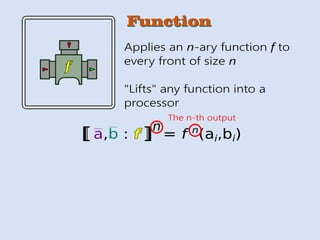
- 37. f FunctionFunction Applies an n-ary function f to every front of size n "Lifts" any function into a processor a,b : f[[ n = f n (ai,bi)
- 38. f FunctionFunction Applies an n-ary function f to every front of size n "Lifts" any function into a processor a,b : f[[ n = f n (ai,bi) The n-th output
- 39. f FunctionFunction Applies an n-ary function f to every front of size n "Lifts" any function into a processor a,b : f[[ n = f n (ai,bi) The n-th output i The i-th event
- 40. f FunctionFunction Applies an n-ary function f to every front of size n "Lifts" any function into a processor a,b : f[[ n = f n (ai,bi) The n-th output i The i-th event f + f <0? Pairwise sum of events Is each event negative?
- 41. CumulativeCumulative Applies a 2 : 1 function f to its previous value and the current event a : Σf[[ = f(x,a1), f(f(x,a1),a2), ... + <Sum of all events Have we seen ⊤ so far? Σ f x Σ f Σ f 0 ⊥
- 42. TrimTrim Returns the input trace, trimmed of its first n events a : [[ = an+1, an+2, ... n n
- 43. TrimTrim Returns the input trace, trimmed of its first n events a : [[ = an+1, an+2, ... n n 1 f =?=? < Σ f ⊥ Does the same number repeat twice in a row?
- 44. GroupGroup Makes a set of connected processors behave as a single processor
- 45. GroupGroup Makes a set of connected processors behave as a single processor 1 f =?=? < Σ f ⊥
- 46. ForkFork Replicates its input on each of its n outputs a : Ψ[[ = a1, a2, ... n
- 47. DecimateDecimate Outputs every n-th input event a : [[ = a1, an+1, a2n+1, ...n Ψ n
- 48. FilterFilter A n : n-1 processor; outputs the n-1 first components of a front if its last component is ⊤; otherwise, discards it a , a , ..., a : =[[ 2 k1 n F i {a if a =⊤ ε otherwise k i n i Powerful mechanism: "anything can be filtered" (don't care about condition) Boolean trace does not need to come from the same source as the inputs being filtered
- 49. FilterFilter A n : n-1 processor; outputs the n-1 first components of a front if its last component is ⊤; otherwise, discards it f <0? Get only the negative events of the input
- 50. WindowWindow Returns the output of a processor P on a sliding window of width n a : Υ =[[ P i Powerful mechanism: "anything can be windowed" (don't care about function) n { n ai, ... ai+n : P[[ *
- 51. WindowWindow Returns the output of a processor P on a sliding window of width n a : Υ =[[ P i Powerful mechanism: "anything can be windowed" (don't care about function) n { n ai, ... ai+n : P[[ * The last event
- 52. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0
- 53. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 3 4 2
- 54. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 3 4 2
- 55. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 3 24
- 56. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 243
- 57. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 2 243
- 58. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 2 243
- 59. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 2 243 4
- 60. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 6 243 2
- 61. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 6 243 23
- 62. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 9 243 6 2
- 63. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 9 243 6 2 3 2 1
- 64. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 9 243 6 2 9
- 65. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 243 9
- 66. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 1 43 9
- 67. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 43 91
- 68. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 43 91 4
- 69. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 43 91 4
- 70. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 43 91 43
- 71. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 43 91 7 4
- 72. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 43 91 7 41
- 73. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 43 91 8 7 4
- 74. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 43 81 8 7 4 9
- 75. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 43 81 9
- 76. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 31 8 9
- 77. WindowWindow Returns the output of a processor P on a sliding window of width n n { 3 {+ Σ f 0 31 8 9 The sum of all 3 successive events
- 78. SliceSlice Dispatches an event e to a distinct instance of processor P according to the value of some function f {a if f(ai)=k ε otherwise i πf k[a : =[i P f[a : =[i U πf k[a1,...ai : [i[ [: P k * +
- 79. SliceSlice Dispatches an event e to a distinct instance of processor P according to the value of some function f {a if f(ai)=k ε otherwise i πf k[a : =[i P f[a : =[i U πf k[a1,...ai : [i[ [: P k * + Multiset union
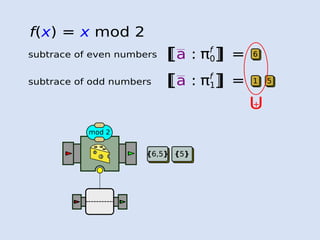
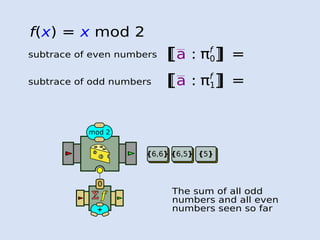
- 80. f(x) = x mod 2
- 81. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers
- 82. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2
- 83. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5
- 84. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5
- 85. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5 U+
- 86. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5 U+ {9}{5}
- 87. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5 U+ {9}{5}
- 88. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5 {9}{5}6
- 89. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5 {9}{5} 6
- 90. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5 {9}{5} 6 U+
- 91. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5 {9}{6,5} 6 U+ {9}{5}
- 92. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5 {9}{6,5} 6 {9}{5}1
- 93. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 5 {9}{6,5} 6 {9}{5} 1
- 94. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 1 {9}{6,5} 6 {9}{5} 5 U+
- 95. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 1 {9}{6,1} 6 {9}{6,5} 5 U+ {5}
- 96. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 1 {9}{6,1} 6 {9}{6,5} 5 U+ {5} The last odd and even numbers seen so far
- 97. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 + Σ f 0
- 98. f(x) = x mod 2 πf 0[a : =[subtrace of even numbers πf 1[a : =[subtrace of odd numbers mod 2 + Σ f 0 The sum of all odd numbers and all even numbers seen so far {9}{6,6} {9}{6,5} {5}
- 99. Input/outputInput/output 0 : 1 processors can be used to produce an event trace out of an external source (i.e. standard input, a file, etc.) Ditto for 1 : 0 processors a . . .b a . . .b
- 100. WARP ZONE
- 101. PalettesPalettes BeepBeep provides only a few built-in processors and functions Palette Set of processors and functions, centered around a particular use case Concretely, a JAR library defining new (reusable!) Processor and Function objects
- 102. Let's put it all toghether! i.e. a few examples of queries from past publications
- 103. Use BeepBeep as a library in your program
- 104. → Fork f = new Fork(2); Use BeepBeep as a library in your program
- 105. → →→ → Fork f = new Fork(2); FunctionProcessor sum = new FunctionProcessor( ); f Use BeepBeep as a library in your program
- 106. → →→ + → Fork f = new Fork(2); FunctionProcessor sum = new FunctionProcessor(Addition.instance); f Use BeepBeep as a library in your program
- 107. → →→ + → Fork f = new Fork(2); FunctionProcessor sum = new FunctionProcessor(Addition.instance); CountDecimate decimate = new CountDecimate(n); f n Use BeepBeep as a library in your program
- 108. → →→ + →→ Fork f = new Fork(2); FunctionProcessor sum = new FunctionProcessor(Addition.instance); CountDecimate decimate = new CountDecimate(n); Connector.connect(fork, LEFT, sum, LEFT) f n Use BeepBeep as a library in your program
- 109. → →→ + → →→ Fork f = new Fork(2); FunctionProcessor sum = new FunctionProcessor(Addition.instance); CountDecimate decimate = new CountDecimate(n); Connector.connect(fork, LEFT, sum, LEFT) .connect(fork, RIGHT, decimate, INPUT) f n Use BeepBeep as a library in your program
- 110. → →→ + → →→ Fork f = new Fork(2); FunctionProcessor sum = new FunctionProcessor(Addition.instance); CountDecimate decimate = new CountDecimate(n); Connector.connect(fork, LEFT, sum, LEFT) .connect(fork, RIGHT, decimate, INPUT) .connect(decimate, OUTPUT, sum, RIGHT); f n Use BeepBeep as a library in your program
- 111. → →→ + → →→ Fork f = new Fork(2); FunctionProcessor sum = new FunctionProcessor(Addition.instance); CountDecimate decimate = new CountDecimate(n); Connector.connect(fork, LEFT, sum, LEFT) .connect(fork, RIGHT, decimate, INPUT) .connect(decimate, OUTPUT, sum, RIGHT); Pullable p = sum.getOutputPullable(OUTPUT); while (p.hasNext() != NextStatus.NO) { Object o = p.next(); ... } f n Use BeepBeep as a library in your program
- 112. → → → ^ n → → → + → → → → → ÷ → →1 → → + Σ Σ 0 0 The statistical moment of order n
- 113. → → → ^ n → → → + → → → → → ÷ → →1 → → + Σ Σ 0 0 The statistical moment of order n → →E(x) n As a group processor
- 114. Trigger an alarm
- 115. → → → → 1 → → > Trigger an alarm when two successive events
- 116. → → → 1 → → → → → <? → → → 1 → → > Trigger an alarm when two successive events are more than 1
- 117. → → → → 1 → → → ÷ → → → → → <? → → → 1 → → →σ → > Trigger an alarm when two successive events are more than 1 standard deviation
- 118. → → → → → 1 → → → - → → → ÷ → → → → → <? → → → 1 → → →E(x) 1 → →σ → > Trigger an alarm when two successive events are more than 1 standard deviation from the mean
- 119. → ⊇? → → → A →→ T ??...<a> <a> ... /a/b //character/id/text() → →
- 120. → → ? ? T /a/b //status/text() =? Walker * /a/b //status/text() =? Blocker * * →→ → /a/b //character → →→ A /a/b //id/text() → T ??...<a> <a> ...
- 121. → A /a/b //character[status=Walker]/id/text() → p1 → A → p2 → → → → /a/b //character[status=Blocker]/id/text() → → → 3 → → → <? → → → → → → → → f1 f2 → → → → → → → /a/b //character[id=p1]/position/x/text() /a/b //character[id=p2]/position/x/text() - |...| <? 6 > ... f1 /a/b //character[id=p1]/position/x/text() /a/b //character[id=p2]/position/x/text() - |...| f2
- 122. → → * * * * Create Auction =? 0 @ Last Price Days 0:= 3@Max. Days :=Min. Price 2@:= Days := Days 1 + End of Day =? 0 @ > <? Days Last Price 2 @:= Bid =? 0 @ > Min. Price <? 2 @ Last Price >? 2 @ Bid =? 0 @ > Last Price >? 2 @ Days := Days 1 + End of Day =? 0 @ Max. Days → End of Day * 1@ * → →→ → * Sold =? 0 @ Days Days + | |.÷
- 123. → → 1@ += Sanitise =? 0 @ Clean := Derive =? 0 @ > ∊ ? Clean T ??...Derive(a,b) Clean 2@ +=Clean := Clean 1 @ Use =? 0 @ > ∊ ? Clean 1 @ T * * T ...
- 124. is used for most projects developed at LIF. We follow stringent backward-compa�bility constraints: all our code compiles on 1.6 is used for archiving and version control. Code is hosted in repositories on git .
- 126. All projects have standardized build scripts.All projects have standardized Automated tests are run with using for con�nuous integra�on. Test results and coverage are tracked through a dashboard on
- 127. $ git clone $ ant download-deps $ ant build $ ant test $ ant javadoc $ ant jar
- 130. So�ware is released under the licences Libraries can be freely used, including in commercial so�ware. Apache or
- 131. Tuples Basic rela�onal algebra NetP Parsing of network packets MTNP Manipulate Tables N'Plots ML Machine Learning, Clustering, Data Mining Let us look at a few pale�es that we will use... h�ps://github.com/liflab/beepbeep-3-pale�es
- 132. 3 8 a 3 8 a 2 6 c Palette Tuples New event type: tuple (set of key-value pairs). Turns an incoming event v into a tuple k=v Turns the value of column x into the header of column yx y k x y Keeps only keys x, y and discards the others Tuple union∪
- 133. Palette NetP New event type: packet. Parses a binary blob into a packet k Fetches header k from packet h�ps://youtu.be/wA0ZIA-6tVE
- 134. In a stream of network packets, what is the set of all source IP addresses? ? ? f src Σ ∅ ∪ f
- 135. In a stream of network packets, what is the set of all source IP addresses? ? ? f src Σ ∅ ∪ f converts blob into packet
- 136. In a stream of network packets, what is the set of all source IP addresses? ? ? f src Σ ∅ ∪ f converts blob into packet fetches source address from packet
- 137. In a stream of network packets, what is the set of all source IP addresses? ? ? f src Σ ∅ ∪ f converts blob into packet fetches source address from packet aggregates addresses into a set
- 138. In a stream of network packets, what is the set of all source IP addresses? ? ? f src Σ ∅ ∪ f ApplyFunction to_packet = new ApplyFunction(PacketParse.instance); ApplyFunction get_src = new ApplyFunction(new GetHeader("src")); Cumulate address_set = new Cumulate(Sets.UNION); connect(to_packet, get_src, address_set);
- 139. { 5m/1m f src dst Σ ∅ ∪ f # Over a window of 5 minutes, how many source IP addresses are associated to each destination address? ? ? →
- 140. In a stream of network packets, what is the cumulative bandwidth for each incoming IP address? ? ? → f size Σ 0 + 1 Σ 0 + f t src f ∪ +
- 141. t 0 1 2 3 ... 10.10.10.1 3 61 61 108 ... 103.1.57.6 - - 89 89 ... The output is a stream of tables, each of which looks like this: �mestamp one column per source IP cumula�ve packet size
- 142. + This table stream can be used as the source of a plot that is dynamically updated. . . . 3
- 143. Palette ML
- 144. <?d { β d δP n
- 146. <?d { β d δP n trend processor Computes a "trend" over a finite sequence of events
- 147. <?d { β d δP n sliding window width The trend is computed over the last n events.
- 148. <?d { β d δP n reference trend Used as a basis for comparison with the current stream
- 149. <?d { β d δP n distance metric Computes the "distance" between the computed trend and the reference
- 150. <?d { β d δP n distance threshold Maximum acceptable distance, according to the selected metric
- 151. <?d { β d δP n comparison func�on Checks if distance is above threshold
- 152. <?d { β d δP n output A stream of Booleans. ⊤ is emi�ed whenever the input stream deviates "too much" from P.
- 153. <?d { β d δP n This pa�ern can be encapsulated into a generic group processor taking 6 parameters. Various computa�ons can be achieved by giving different values to these parameters.
- 154. β i f #
- 155. β i f # Calculates the number of dis�nct symbols in the input stream iden�ty func�on map size map symbol → # occurrences
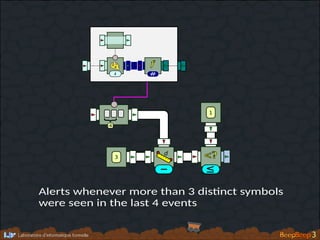
- 156. β i f # n 4 3 P δ - 1 d ≤
- 157. <?d { 3 4 i f # 1 - ≤ Alerts whenever more than 3 dis�nct symbols were seen in the last 4 events
- 158. Group counter = new Group(1, 1); { SlicerMap slicer = new SlicerMap( new IdentityFunction(1), new Passthrough(1)); counter.associateInput(INPUT, slicer, INPUT); ApplyFunction size = new ApplyFunction(Maps.Size); connect(slicer, size); counter.associateOutput(OUTPUT, size, OUTPUT); counter.addProcessors(slicer, size); } TrendDistance<> alarm = new TrendDistance<HashMap,Number,Number>( 3, 4, slicer, Numbers.Subtraction, 1, Numbers.IsLessThan); 8 lines of code
- 159. β f Σ 0 + Σ 0 + ÷ 1
- 160. β f Σ 0 + Σ 0 + ÷ 1 Calculates the running average of the input stream... ...i.e. the average of all values seen so far
- 161. β f Σ 0 + Σ 0 + ÷ 1 n 3 6 P δ ½ d ≤ | | 21 −
- 162. β f Σ 0 + Σ 0 + ÷ 1 n 3 6 P δ ½ d ≤ | | 21 − 21ABS( − ) Manha�an Distance of dimension 1
- 163. <?d { 6 3 ½ ≤ Alerts whenever the running average of the last 3 events deviates by more than ½ from 6 f Σ 0 + Σ 0 + ÷ 1 | | 21 −
- 164. <?d { 6 3 ½ ≤ Alerts whenever the running average of the last 3 events deviates by more than ½ from 6 f Σ 0 + Σ 0 + ÷ 1 | | 21 − 15 lines of code
- 165. β i Σ 0 + 1
- 166. β i Σ 0 + 1 Calculates the number of occurrences of each symbol in the input stream non-normalized probability density func�on a b c 3 1 5
- 168. n 9 P δ 2 d ≤ a b c 6 1 2 Reference pa�ern is a distribu�on (Manha�an) map distance func�on a b c 6 1 2 a b c 3 4 1 = |6−3|+|1−4|+|2−1| = 7
- 170. <?d { 9 2 ≤ Alerts whenever the distribu�on of the last 9 events is at a Manha�an map distance of more than 2 from the reference distribu�on i Σ 0 + 1 a b c 6 1 2
- 171. <?d { 9 2 ≤ Alerts whenever the distribu�on of the last 9 events is at a Manha�an map distance of more than 2 from the reference distribu�on i Σ 0 + 1 a b c 6 1 2 9 lines of code
- 172. f src dst Σ ∅ ∪ f # β In a stream of network packets, calculates the number of source addresses associated to each des�na�on address 10.1.104.32 103.208.1.2 15.61.6.80 ... 6 11 24 ... a "distribu�on"
- 174. n 10 min P δ 30 d ≤ 10.1.104.32 103.208.1.2 15.61.6.80 ... 6 11 24 ... Maximum map distance func�on a b c 6 1 2 a b c 3 4 1 = {|6−3|,|1−4|,|2−1|} = 3max
- 176. <?d { 30 ≤ Alerts whenever, in a window of 10 minutes, the number of source addresses for some des�na�on IP address deviates by more than 30 from the reference distribu�on f src dst Σ ∅ ∪ f # 10.1.104.32 103.208.1.2 15.61.6.80 ... 6 11 24 ... 10m/10m
- 177. <?d { β d δP n So far, the reference trend has been a single object.
- 178. What if there could be mul�ple possible trends? PP mul�modal trend <?d { β d δP n So far, the reference trend has been a single object.
- 179. Given a finite set of points P = {p1,p2,...}, define func�on: Δ min p'∈P Δ(p,p')(p) = It is the distance between p and the closest point in P. Δ can be any distance metric: Euclidean distance, Manha�an distance, etc. p1 p2 p3
- 180. β f Σ 0 + Σ 0 + ÷ 1 n 3 6 P δ ½ d ≤ | | 21 − "Alerts whenever the running average of the last 3 events deviates by more than ½ from 6"
- 181. β f Σ 0 + Σ 0 + ÷ 1 n 3 6 P δ ½ d ≤ | | 21 − {6,9} P δ | | 21 − "Alerts whenever the running average of the last 3 events deviates by more than ½ from 6 and 9"
- 182. 3 4 5 6 7 8 9 10 11 ...... In this case, the func�on , along with and , defines two 1-dimensional "balls" of radius ½. The alarm is triggered when the running average does not lie within one of these balls. P d
- 183. 3 4 5 6 7 8 9 10 11 ...... In this case, the func�on , along with and , defines two 1-dimensional "balls" of radius ½. The alarm is triggered when the running average does not lie within one of these balls. P d 6.1, 6.0, 6.2 6.1 x ✓
- 184. 3 4 5 6 7 8 9 10 11 ...... In this case, the func�on , along with and , defines two 1-dimensional "balls" of radius ½. The alarm is triggered when the running average does not lie within one of these balls. P d 6.1, 6.0, 6.2 6.1 x ✓ 7.3, 8.9, 7.5 7.9 x ✗
- 185. 3 4 5 6 7 8 9 10 11 ...... In this case, the func�on , along with and , defines two 1-dimensional "balls" of radius ½. The alarm is triggered when the running average does not lie within one of these balls. P d 6.1, 6.0, 6.2 6.1 x ✓ 7.3, 8.9, 7.5 7.9 x ✗ Mul�-modal trends can also be mul�-dimensional!
- 186. Consider streams of symbols a and b. i Σ 0 + 1 f DP Σ=1 [ ] 1
- 187. Consider streams of symbols a and b. i Σ 0 + 1 f DP Σ=1 [ ] 1 computes a map of the number of occurrences of a and b extracts the map's values normalizes the vector casts into DoublePoint
- 188. Consider streams of symbols a and b. i Σ 0 + 1 f DP Σ=1 [ ] 1 The output is a two-dimensional point (or vector) ( 0.33, 0.66 ) frac�on of a's frac�on of b's
- 189. Consider streams of symbols a and b. Suppose that the observed streams fall in two categories: a,a,a,a,b,a,b,a,b,a a,a,a,a,a,b,b,a,a,b b,b,a,a,a,b,a,a,a,a Roughly 70% of a, 30% of b a,b,a,b,b,b,b,b,b,a b,b,b,b,a,a,b,b,a,b b,a,b,b,b,b,b,b,a,a Roughly 30% of a, 70% of b ( 0.7, 0.3 ) ( 0.3, 0.7 ) 1 2
- 190. Streams can be seen as two-dimensional points: Fraction of a's Fractionofb's 0% 100% 100% 1 2 (0.7,0.3) (0.3,0.7)
- 191. β i Σ 0 + 1 f DP Σ=1 [ ] 1 n P δ .15 d ≤9 ΔE (0.3,0.7) (0.7,0.3) { }
- 192. <?d { 9 .15 ≤ ΔE (0.3,0.7) (0.7,0.3) { } i Σ 0 + 1 f DP Σ=1 [ ] 1 Alerts whenever the distribu�on of the last 9 events is further than .15 from either category
- 194. Fraction of a's Fractionofb's a,a,b,a,a,b,a,b,a ( 0.67, 0.33 )p= p
- 195. Fraction of a's Fractionofb's a,a,b,a,a,b,a,b,a ( 0.67, 0.33 )p= p d=0.047✓
- 196. Fraction of a's Fractionofb's b,a,b,a,b,a,b,a,b ( 0.44, 0.56 )p= p
- 197. Fraction of a's Fractionofb's b,a,b,a,b,a,b,a,b ( 0.44, 0.56 )p= p d=0.2 This stream is "too different" from either category or !1 2 ✗
- 198. Group vector = new Group(1, 1); { Group counter = new Group(1, 1); { Constant one = new Constant(1); counter.associateInput(INPUT, one, INPUT); Cumulate sum_one = new Cumulate(new CumulativeFunction<Number>(Numbers.Addition)); connect(one, sum_one); counter.associateOutput(OUTPUT, sum_one, OUTPUT); counter.addProcessors(one, sum_one); } SlicerMap slicer = new SlicerMap(new IdentityFunction(1), counter); ApplyFunction to_normalized_vector = new ApplyFunction( new FunctionTree(DoublePointCast.instance, new FunctionTree(Normalize.instance, new FunctionTree(ToValueArray.instance, new StreamVariable(0))))); connect(slicer, to_normalized_vector); vector.associateInput(INPUT, slicer, INPUT); vector.associateOutput(OUTPUT, to_normalized_vector, OUTPUT); vector.addProcessors(slicer, to_normalized_vector); } Multiset pattern = new Multiset(); pattern.add(new DoublePoint(new double[]{0.7, 0.3})) .add(new DoublePoint(new double[]{0.3, 0.7})); TrendDistance<> alarm = new TrendDistance<Multiset,Multiset,Number>(pattern, 9, vector, new FunctionTree(AbsoluteValue.instance, new FunctionTree( new DistanceToClosest(new EuclideanDistance()), new StreamVariable(0), new StreamVariable(1))), 0.15, Numbers.IsLessThan);
- 199. Group vector = new Group(1, 1); { Group counter = new Group(1, 1); { Constant one = new Constant(1); counter.associateInput(INPUT, one, INPUT); Cumulate sum_one = new Cumulate(new CumulativeFunction<Number>(Numbers.Addition)); connect(one, sum_one); counter.associateOutput(OUTPUT, sum_one, OUTPUT); counter.addProcessors(one, sum_one); } SlicerMap slicer = new SlicerMap(new IdentityFunction(1), counter); ApplyFunction to_normalized_vector = new ApplyFunction( new FunctionTree(DoublePointCast.instance, new FunctionTree(Normalize.instance, new FunctionTree(ToValueArray.instance, new StreamVariable(0))))); connect(slicer, to_normalized_vector); vector.associateInput(INPUT, slicer, INPUT); vector.associateOutput(OUTPUT, to_normalized_vector, OUTPUT); vector.addProcessors(slicer, to_normalized_vector); } Multiset pattern = new Multiset(); pattern.add(new DoublePoint(new double[]{0.7, 0.3})) .add(new DoublePoint(new double[]{0.3, 0.7})); TrendDistance<> alarm = new TrendDistance<Multiset,Multiset,Number>(pattern, 9, vector, new FunctionTree(AbsoluteValue.instance, new FunctionTree( new DistanceToClosest(new EuclideanDistance()), new StreamVariable(0), new StreamVariable(1))), 0.15, Numbers.IsLessThan); 17 lines of code
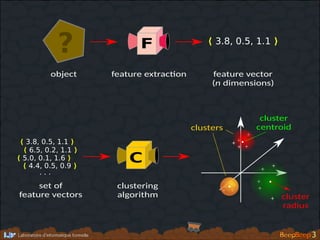
- 200. object (e.g. stream) feature extrac�on feature vector (n dimensions) ? ⟨ 3.8, 0.5, 1.1 ⟩F A recurring process in data mining: Examples of feature vectors: Distribu�on of symbols Sta�s�cal moments Any other numerical computa�on
- 201. <?d{ β d δP n But where does this reference trend come from? ?
- 202. <?d{ β d δ n Op�on #1: it is computed from the stream itself. {m β
- 203. <?d{ β d δ n Op�on #1: it is computed from the stream itself. {m β fork The stream is split in two
- 204. <?d{ β d δ n Op�on #1: it is computed from the stream itself. {m β reference trend The reference is computed over a window of width m
- 205. <?d{ β d δ n Op�on #1: it is computed from the stream itself. {m β stream offset Second stream copy is trimmed of its first m events
- 206. <?d{ β d δ n Op�on #1: it is computed from the stream itself. {m β The rest of the pipe works as before
- 207. m n Trend from "the present" Trend from "the past" vs. β β An alarm is triggered when the stream's current trend becomes "too different" from what it was in the past ⇒ self-correla�on
- 208. { <?d { β d δ nm This pa�ern can be encapsulated into a generic group processor taking 6 parameters.
- 209. { <?d { β d δ nm This pa�ern can be encapsulated into a generic group processor taking 6 parameters. Self-Correlated Trend Distance (SCTD)
- 211. { <?d { 6 ≤| | 21 − 6 3 1 f Σ 0 + Σ 0 + ÷ 1 Alerts whenever the running average of the last 3 events deviates by more than 1 from the running average of the 6 before
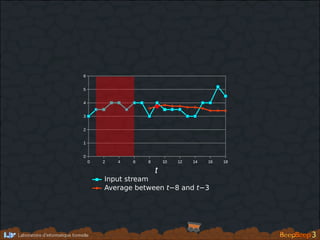
- 212. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream
- 213. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3
- 214. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3
- 215. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3
- 216. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3
- 217. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3 Average between t−2 and t
- 218. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3 Average between t−2 and t
- 219. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3 Average between t−2 and t
- 220. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3 Average between t−2 and t
- 221. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3 Average between t−2 and t Manhattan distance between averages
- 222. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream Average between t−8 and t−3 Average between t−2 and t Manhattan distance between averages threshold exceeded
- 223. 0 2 4 6 8 10 12 14 16 18 0 1 2 3 4 5 6 t Input stream The average in this window ("the past") the average in this window ("the present") is too far from
- 224. + object feature extrac�on feature vector (n dimensions) ? ⟨ 3.8, 0.5, 1.1 ⟩F ⟨ 3.8, 0.5, 1.1 ⟩ ⟨ 6.5, 0.2, 1.1 ⟩ ⟨ 5.0, 0.1, 1.6 ⟩ ⟨ 4.4, 0.5, 0.9 ⟩ . . . set of feature vectors C clustering algorithm + + + + + + + + ++ + + + + clusters cluster centroid cluster radius
- 225. <?d{ β d δP n But where does this reference trend come from? ?
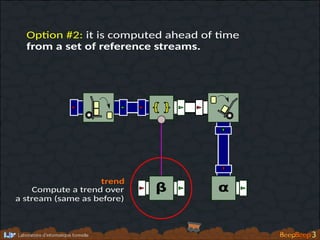
- 226. β α }{ α Op�on #2: it is computed ahead of �me from a set of reference streams.
- 227. β α }{ α Op�on #2: it is computed ahead of �me from a set of reference streams. Unpacks a set of streams and feeds them one by one unpacking
- 228. β α }{ α Op�on #2: it is computed ahead of �me from a set of reference streams. Feed each event of a stream to a processor and collect its last output dropping
- 229. β α }{ α Op�on #2: it is computed ahead of �me from a set of reference streams. Compute a trend over a stream (same as before) trend
- 230. β α }{ α Op�on #2: it is computed ahead of �me from a set of reference streams. Collate trend objects from all streams into a set pack
- 231. β α }{ α Op�on #2: it is computed ahead of �me from a set of reference streams. Compute a global trend object from all individual trends aggregate
- 232. β α }{ α This process can be encapsulated into a generic group processor with 2 parameters.
- 234. β f Σ 0 + Σ 0 + ÷ 1 α f Σ 0 + Σ 0 + ÷ 1 running average of a stream average of values in a set
- 237. }{ f Σ 0 + Σ 0 + ÷ 1 f Σ 0 + Σ 0 + ÷ 1 {⟨1,2,1,1⟩, ⟨2,2,1,2⟩, ⟨3,1,1,1⟩} a set of 3 streams 1,2,1,1 1¼ {1¼}
- 238. }{ f Σ 0 + Σ 0 + ÷ 1 f Σ 0 + Σ 0 + ÷ 1 {⟨1,2,1,1⟩, ⟨2,2,1,2⟩, ⟨3,1,1,1⟩} a set of 3 streams 2,2,1,2 1¾ {1¼,1¾}
- 239. }{ f Σ 0 + Σ 0 + ÷ 1 f Σ 0 + Σ 0 + ÷ 1 {⟨1,2,1,1⟩, ⟨2,2,1,2⟩, ⟨3,1,1,1⟩} a set of 3 streams 3,1,1,1 1½ {1¼,1¾,1½}
- 240. }{ f Σ 0 + Σ 0 + ÷ 1 f Σ 0 + Σ 0 + ÷ 1 {⟨1,2,1,1⟩, ⟨2,2,1,2⟩, ⟨3,1,1,1⟩} a set of 3 streams 1½ {1¼,1¾,1½} the average of all running averages
- 241. + object feature extrac�on feature vector (n dimensions) ? ⟨ 3.8, 0.5, 1.1 ⟩F ⟨ 3.8, 0.5, 1.1 ⟩ ⟨ 6.5, 0.2, 1.1 ⟩ ⟨ 5.0, 0.1, 1.6 ⟩ ⟨ 4.4, 0.5, 0.9 ⟩ . . . set of feature vectors C clustering algorithm + + + + + + + + ++ + + + + clusters cluster centroid cluster radius
- 242. C The ML pale�e uses Apache Commons Mαth][which supports the following clustering algorithms: , K-Means++ C Fuzzy-K-Means C DBSCAN C Mul�-K-Means++ h�ps://commons.apache.org/proper/commons-math/userguide/ml.html
- 243. β α }{ α
- 244. F C }{
- 245. β f Σ 0 + Σ 0 + ÷ 1 α f 2 running average of a stream K-means func�on (with K=2)
- 247. }{ f Σ 0 + Σ 0 + ÷ 1 f 2 {⟨5,6,5,6,7,6⟩, ⟨8,9,8,10,9⟩, ⟨6,6,7,6,6,5⟩, ⟨7,6,6,7,6,6,5⟩, ⟨9,8,10,9⟩} a set of streams
- 248. }{ f Σ 0 + Σ 0 + ÷ 1 f 2 {⟨5,6,5,6,7,6⟩, ⟨8,9,8,10,9⟩, ⟨6,6,7,6,6,5⟩, ⟨7,6,6,7,6,6,5⟩, ⟨9,8,10,9⟩} a set of streams {5.83, 8.8, 6.0, 6.14, 9} set of running averages
- 249. }{ f Σ 0 + Σ 0 + ÷ 1 f 2 {⟨5,6,5,6,7,6⟩, ⟨8,9,8,10,9⟩, ⟨6,6,7,6,6,5⟩, ⟨7,6,6,7,6,6,5⟩, ⟨9,8,10,9⟩} a set of streams {5.83, 8.8, 6.0, 6.14, 9} set of running averages {5.99, 8.9} cluster centroids 5 6 7 8 9 10 11 ......
- 250. β α f 2 distribu�on of symbols K-means func�on (with K=2) i Σ 0 + 1 f DP Σ=1 [ ] 1
- 254. }{ f 2 i Σ 0 + 1 f DP Σ=1 [ ] 1 a,a,a,a,b,a,b,a,b,a a,a,a,a,a,b,b,a,a,b b,b,a,a,a,b,a,a,a,a a,b,a,b,b,b,b,b,b,a b,b,b,b,a,a,b,b,a,b b,a,b,b,b,b,b,b,a,a { } (0.7,0.3), (0.3,0.7), (0.7,0.3), (0.7,0.3), (0.3,0.7), (0.3,0.7) { } cluster centroids { (0.7,0.3), (0.3,0.7) } Fraction of a's Fractionofb's (0.7,0.3) (0.3,0.7)
- 255. Kyoto Dataset 56.621025 http 951 6552 4 1.00 0.00 0.00 21 21 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1670 fda2:69aa:1f1a:8fd3:358b:171c:73a3:0322 80 17:33:20 tcp 55.135794 http 1095 56999 0 0.00 0.00 0.00 15 15 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1675 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:22 tcp 0.368001 other 4 0 0 0.00 0.00 0.00 100 100 1.00 0.00 0.00 OTH 0 0 0 -1 fda2:69aa:1f1a:ac6d:7dc6:27b2:07ae:05ec 445 fda2:69aa:1f1a:f8aa:7da2:088f:3b04:1912 18 17:33:28 tcp 46.495270 http 501 676 0 0.00 0.00 0.00 16 16 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1680 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:30 tcp 46.495394 http 481 652 1 1.00 0.00 0.00 17 17 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1678 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:30 tcp 46.502517 http 468 507 2 1.00 0.00 0.00 18 18 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1679 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:30 tcp 46.503890 http 501 614 3 1.00 0.00 0.00 19 19 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1681 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:30 tcp h�p://www.takakura.com/Kyoto_data/
- 256. Kyoto Dataset 56.621025 http 951 6552 4 1.00 0.00 0.00 21 21 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1670 fda2:69aa:1f1a:8fd3:358b:171c:73a3:0322 80 17:33:20 tcp 55.135794 http 1095 56999 0 0.00 0.00 0.00 15 15 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1675 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:22 tcp 0.368001 other 4 0 0 0.00 0.00 0.00 100 100 1.00 0.00 0.00 OTH 0 0 0 -1 fda2:69aa:1f1a:ac6d:7dc6:27b2:07ae:05ec 445 fda2:69aa:1f1a:f8aa:7da2:088f:3b04:1912 18 17:33:28 tcp 46.495270 http 501 676 0 0.00 0.00 0.00 16 16 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1680 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:30 tcp 46.495394 http 481 652 1 1.00 0.00 0.00 17 17 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1678 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:30 tcp 46.502517 http 468 507 2 1.00 0.00 0.00 18 18 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1679 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:30 tcp 46.503890 http 501 614 3 1.00 0.00 0.00 19 19 0.00 0.00 0.00 RSTO 0 0 0 -1 fda2:69aa:1f1a:3aef:7af3:3027:3045:7ff2 1681 fda2:69aa:1f1a:e591:334a:006d:0292:71a0 80 17:33:30 tcp h�p://www.takakura.com/Kyoto_data/ Features can be computed by BeepBeep on a raw packet capture
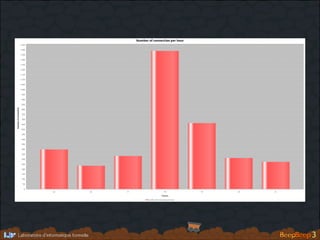
- 257. Compute distribu�on of number of connec�ons per hour of the day h�ps://youtu.be/_Pc3Q_RiFaw
- 259. Compute rela�ve frequency of TCP ports h�ps://youtu.be/1hdtWCpc0Xk
- 260. Port 80
- 261. Plo�ng and clustering of session dura�on vs. �me of the day h�ps://youtu.be/DLJJDjXCeeQ
- 263. Perform K-means clustering on the dura�on of each session h�ps://youtu.be/aOnzSMK-E38
- 265. P Flimit f f (x,y) getSourceBytes getDestinationBytes [ ] [ ] f ScatterPlotGenerator f KMeansSmart filePath kk refreshInterval Perform k-means clustering over bytes sent/received by each session h�ps://youtu.be/gA_OSVv2Q0g
- 267. All the examples use the same generic pa�ern, yet amount to very different calcula�ons We only need to select (from a list of choices) a few values, func�ons and processors Key observation Predefined queries hard-coded into system Users write custom queries in code Users write custom queries in a custom language FIXED FLEXIBLE EASY HARD This can be turned into a wizard!
- 268. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the data mining pattern you wish to instantiate. Self-correlated trend distance Evaluates the similarity of a trend computed on the present with the same trend computed over a past window. Pattern-based trend distance Evaluates the similarity of a trend computed on the present with a reference trend provided externally.
- 269. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the data mining pattern you wish to instantiate. Self-correlated trend distance Evaluates the similarity of a trend computed on the present with the same trend computed over a past window. Pattern-based trend distance Evaluates the similarity of a trend computed on the present with a reference trend provided externally. { <?d {
- 270. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the input stream to use as the source Pre-recorded log Reads a stream from a file or a named pipe Standard input Reads input events from stdin TCP connection Captures packets from a local TCP port Browse... No file selected Port { <?d {
- 271. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the input stream to use as the source Pre-recorded log Reads a stream from a file or a named pipe Standard input Reads input events from stdin TCP connection Captures packets from a local TCP port Browse... No file selected Port stdin { <?d {
- 272. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the time windows for the evaluation of the pattern Past window (m) Width of the window where the past trend is computed Present window (n) Width of the window where the present trend is computed Change... Currently 1hr 0min 0sec Change... Currently 1hr 0min 0sec stdin { <?d {
- 273. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the time windows for the evaluation of the pattern Past window (m) Width of the window where the past trend is computed Present window (n) Width of the window where the present trend is computed Change... Currently 1hr 0min 0sec Change... Currently 1hr 0min 0sec stdin { <?d { 1h1h 1h 1h
- 274. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the element of each event to use for computing the trend Select the trend to compute over the stream Running average The average of the stream over the entire window Vector of moments The n first statistical moments over the entire window Distinct occurrences The number of distinct values observed in the window Value distribution The distribution of values observed in the window Cumulative sum The sum of all values over the window Direct value Size Other Source Destination 2 stdin { <?d { 1h1h 1h 1h
- 275. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the element of each event to use for computing the trend Select the trend to compute over the stream Running average The average of the stream over the entire window Vector of moments The n first statistical moments over the entire window Distinct occurrences The number of distinct values observed in the window Value distribution The distribution of values observed in the window Cumulative sum The sum of all values over the window Direct value Size Other Source Destination 2 stdin { <?d { 1h1h 1h 1h i Σ 0 + 1 f src
- 276. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the distance metric for comparing the present and the past trends Manhattan distance Sum of pairwise absolute differences in each dimension Euclidean distance Geometrical distance in n dimensions Scalar difference Plain subtraction of two numbers Ratio Plain division of two numbers stdin { <?d { 1h1h 1h 1h i Σ 0 + 1 f src
- 277. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Select the distance metric for comparing the present and the past trends Manhattan distance Sum of pairwise absolute differences in each dimension Euclidean distance Geometrical distance in n dimensions Scalar difference Plain subtraction of two numbers Ratio Plain division of two numbers stdin { <?d { 1h1h 1h 1h i Σ 0 + 1 f src
- 278. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Trigger an alarm when the distance becomes the following threshold: Smaller than Larger than 0.5 stdin { <?d { 1h1h 1h 1h i Σ 0 + 1 f src
- 279. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Trigger an alarm when the distance becomes the following threshold: Smaller than Larger than 0.5 stdin { <?d { 1h1h 1h 1h ½ ≤ i Σ 0 + 1 f src
- 280. Next >< Back BeepBeep Data Mining Wizard 1. Pattern 2. Input stream 3. Windows 4. Trend 5. Distance 6. Threshold Start< Back To summarize, you requested the following data mining operation: Next >Save... Over a stream coming from the standard input, extract a field called Source, and compare the distribution of unique values between the last 1hr 0min 0sec and the 1hr 0min 0sec that precedes it. Raise an alert whenever the Manhattan distance between them exceeds the value of 0.5. stdin { <?d { 1h1h 1h 1h ½ ≤ i Σ 0 + 1 f src
- 281. BeepBeep provides mul�ple func�onali�es for performing data mining on event streams... distance metrics | | 21 − ΔE processor pipes i Σ 0 + 1 f size Σ 0 + 1 Σ 0 + f t src f ∪ + f 2 clustering algorithms ...and easy means of crea�ng custom objects. k x y event types and manipula�on func�ons






















































































































![→
A
/a/b
//character[status=Walker]/id/text()
→ p1
→
A
→ p2
→ →
→
→
/a/b
//character[status=Blocker]/id/text()
→ →
→
3
→
→
→
<?
→
→
→
→
→
→
→
→
f1
f2
→
→ →
→
→
→
→
/a/b
//character[id=p1]/position/x/text()
/a/b
//character[id=p2]/position/x/text()
-
|...|
<?
6
>
...
f1
/a/b
//character[id=p1]/position/x/text()
/a/b
//character[id=p2]/position/x/text()
-
|...|
f2](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-121-320.jpg)































































![Consider streams of symbols a and b.
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-186-320.jpg)
![Consider streams of symbols a and b.
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1
computes a
map of the number
of occurrences of
a and b
extracts the
map's values
normalizes the vector
casts into DoublePoint](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-187-320.jpg)
![Consider streams of symbols a and b.
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1
The output is a two-dimensional point
(or vector)
( 0.33, 0.66 )
frac�on
of a's frac�on
of b's](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-188-320.jpg)


![β
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1
n P δ
.15
d
≤9 ΔE
(0.3,0.7)
(0.7,0.3)
{
}](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-191-320.jpg)
![<?d
{
9
.15
≤
ΔE
(0.3,0.7)
(0.7,0.3)
{
}
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1
Alerts whenever the distribu�on of the last 9
events is further than .15 from either category](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-192-320.jpg)





![Group vector = new Group(1, 1); {
Group counter = new Group(1, 1); {
Constant one = new Constant(1);
counter.associateInput(INPUT, one, INPUT);
Cumulate sum_one = new Cumulate(new CumulativeFunction<Number>(Numbers.Addition));
connect(one, sum_one);
counter.associateOutput(OUTPUT, sum_one, OUTPUT);
counter.addProcessors(one, sum_one);
}
SlicerMap slicer = new SlicerMap(new IdentityFunction(1), counter);
ApplyFunction to_normalized_vector = new ApplyFunction(
new FunctionTree(DoublePointCast.instance,
new FunctionTree(Normalize.instance,
new FunctionTree(ToValueArray.instance, new StreamVariable(0)))));
connect(slicer, to_normalized_vector);
vector.associateInput(INPUT, slicer, INPUT);
vector.associateOutput(OUTPUT, to_normalized_vector, OUTPUT);
vector.addProcessors(slicer, to_normalized_vector);
}
Multiset pattern = new Multiset();
pattern.add(new DoublePoint(new double[]{0.7, 0.3}))
.add(new DoublePoint(new double[]{0.3, 0.7}));
TrendDistance<> alarm = new TrendDistance<Multiset,Multiset,Number>(pattern, 9, vector,
new FunctionTree(AbsoluteValue.instance, new FunctionTree(
new DistanceToClosest(new EuclideanDistance()), new StreamVariable(0),
new StreamVariable(1))), 0.15, Numbers.IsLessThan);](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-198-320.jpg)
![Group vector = new Group(1, 1); {
Group counter = new Group(1, 1); {
Constant one = new Constant(1);
counter.associateInput(INPUT, one, INPUT);
Cumulate sum_one = new Cumulate(new CumulativeFunction<Number>(Numbers.Addition));
connect(one, sum_one);
counter.associateOutput(OUTPUT, sum_one, OUTPUT);
counter.addProcessors(one, sum_one);
}
SlicerMap slicer = new SlicerMap(new IdentityFunction(1), counter);
ApplyFunction to_normalized_vector = new ApplyFunction(
new FunctionTree(DoublePointCast.instance,
new FunctionTree(Normalize.instance,
new FunctionTree(ToValueArray.instance, new StreamVariable(0)))));
connect(slicer, to_normalized_vector);
vector.associateInput(INPUT, slicer, INPUT);
vector.associateOutput(OUTPUT, to_normalized_vector, OUTPUT);
vector.addProcessors(slicer, to_normalized_vector);
}
Multiset pattern = new Multiset();
pattern.add(new DoublePoint(new double[]{0.7, 0.3}))
.add(new DoublePoint(new double[]{0.3, 0.7}));
TrendDistance<> alarm = new TrendDistance<Multiset,Multiset,Number>(pattern, 9, vector,
new FunctionTree(AbsoluteValue.instance, new FunctionTree(
new DistanceToClosest(new EuclideanDistance()), new StreamVariable(0),
new StreamVariable(1))), 0.15, Numbers.IsLessThan);
17 lines of code](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-199-320.jpg)







































![C
The ML pale�e uses Apache Commons Mαth][which supports the following
clustering algorithms:
,
K-Means++
C Fuzzy-K-Means
C DBSCAN
C Mul�-K-Means++
h�ps://commons.apache.org/proper/commons-math/userguide/ml.html](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-242-320.jpg)







![β α
f
2
distribu�on of
symbols
K-means func�on
(with K=2)
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-250-320.jpg)
![}{ f
2
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-251-320.jpg)
![}{ f
2
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1
a,a,a,a,b,a,b,a,b,a
a,a,a,a,a,b,b,a,a,b
b,b,a,a,a,b,a,a,a,a
a,b,a,b,b,b,b,b,b,a
b,b,b,b,a,a,b,b,a,b
b,a,b,b,b,b,b,b,a,a
{
}](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-252-320.jpg)
![}{ f
2
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1
a,a,a,a,b,a,b,a,b,a
a,a,a,a,a,b,b,a,a,b
b,b,a,a,a,b,a,a,a,a
a,b,a,b,b,b,b,b,b,a
b,b,b,b,a,a,b,b,a,b
b,a,b,b,b,b,b,b,a,a
{
}
(0.7,0.3),
(0.3,0.7),
(0.7,0.3),
(0.7,0.3),
(0.3,0.7),
(0.3,0.7)
{
}](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-253-320.jpg)
![}{ f
2
i
Σ
0
+
1
f
DP
Σ=1
[ ]
1
a,a,a,a,b,a,b,a,b,a
a,a,a,a,a,b,b,a,a,b
b,b,a,a,a,b,a,a,a,a
a,b,a,b,b,b,b,b,b,a
b,b,b,b,a,a,b,b,a,b
b,a,b,b,b,b,b,b,a,a
{
}
(0.7,0.3),
(0.3,0.7),
(0.7,0.3),
(0.7,0.3),
(0.3,0.7),
(0.3,0.7)
{
}
cluster
centroids
{ (0.7,0.3),
(0.3,0.7) }
Fraction of a's
Fractionofb's
(0.7,0.3)
(0.3,0.7)](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-254-320.jpg)









![P Flimit
f
f
(x,y)
getSourceBytes
getDestinationBytes
[ ]
[ ]
f
ScatterPlotGenerator
f
KMeansSmart
filePath
kk
refreshInterval
Perform k-means clustering over bytes sent/received
by each session
h�ps://youtu.be/gA_OSVv2Q0g](https://image.slidesharecdn.com/merged-180208202536/85/Mining-event-streams-with-BeepBeep-3-265-320.jpg)















