![Shape matching via CDF I-divergences
Model each point-set by a cumulative distribution function
(CDF)
Quantify the distance among cdfs via an information-theoretic
measure [typically the cumulative residual entropy (CRE)]
Minimize the dis-similarity measure over the space of
coordinate transformation parameters
14/29](https://image.slidesharecdn.com/l5shape-matching-idivergencescvpr-110515222124-phpapp02/85/CVPR2010-Advanced-ITinCVPR-in-a-Nutshell-part-5-Shape-Matching-and-Divergences-20-320.jpg)
CVPR2010: Advanced ITinCVPR in a Nutshell: part 5: Shape, Matching and Divergences
- 1. A vne da cd Ifr t nT e r i nomai h oyn o C P “ aN t e” VRi n us l hl CP VR T ti u rl oa J n 1 -82 1 u e 31 0 0 S nFa c c ,A a rn i oC s Shape Matching with I-divergences Anand Rangarajan
- 2. Shape Matching with I-Divergences Groupwise Point-set Pattern Registration Given N point-sets, which are denoted by {X p , p ∈ {1, ..., N}}, the task of multiple point pattern matching or point-set registration is to recover the spatial transformations which yield the best alignment of all shapes. 2/29
- 3. Problem Visualization 3/29
- 4. Problem Visualization 3/29
- 5. Group-wise Point-set Registration Principal Technical Challenges Solving for nonrigid deformations between point-sets with unknown correspondence is a difficult problem. How do we align all the point-sets in a symmetric manner so that there is no bias toward any particular point-set? 4/29
- 6. From point-sets to density functions 5/29
- 7. From point-sets to density functions 5/29
- 8. Group-wise Point-set Registration From point-sets to density functions Point sets are represented by probability density functions. Intuitively, if these point sets are aligned properly, the corresponding density functions should be similar. 6/29
- 9. Group-wise Point-set Registration From point-sets to density functions Point sets are represented by probability density functions. Intuitively, if these point sets are aligned properly, the corresponding density functions should be similar. Question: How do we measure the similarity between multiple density functions? 6/29
- 10. Divergence Measures Kullback-Leibler divergence ˆ p(x) DKL (p q) = p(x) log dx q(x) where p(x), q(x) are the probability density functions. 7/29
- 11. Divergence Measures Kullback-Leibler divergence J divergence ˆ Given two probability density p(x) function p and q, the symmetric KL DKL (p q) = p(x) log dx q(x) divergence is defined as: where p(x), q(x) are the probability 1 J(p, q) = (DKL (p q) + DKL (q p)) density functions. 2 7/29
- 12. Motivating the JS divergence Modeling two shapes X Y N1 K1 N2 K2 (1) 1 (1) (2) 1 (2) p(X |θ )= p(Xi |θa ), p(Y |θ )= p(Yj |θb ) K1 K2 i=1 a=1 j=1 b=1 8/29
- 13. Motivating the JS divergence Modeling the overlay of two shapes with identity of origin X Y p(X ∪ Y |θ(1) , θ(2) ) = p(X |θ(1) )p(Y |θ(2) ) 8/29
- 14. Motivating the JS divergence Modeling the overlay of two shapes without identity of origin Z N1 N2 p(Z |θ(1) , θ(2) ) = p(Z |θ(1) ) + p(Z |θ(2) ) N1 + N2 N1 + N2 8/29
- 15. Likelihood Ratio Which generative model do you prefer? The union of disparate shapes where identity of origin is preserved or one combined shape where the identity of origin is suppressed. Likelihood ratio: N1 (1) N2 (2) p(Z |θ(1) , θ(2) ) N1 +N2 p(Z |θ ) + N1 +N2 p(Z |θ ) log Λ = log = p(X ∪ Y |θ(1) , θ(2) ) p(X |θ(1) )p(Y |θ(2) ) Z is understood to arise from a convex combination of two mixture models p(Z |θ(1) ) and p(Z |θ(2) ) where the weights of each mixture are proportional to the number of points N1 and N2 in each set. Weak law of large numbers leads to Jensen-Shannon divergence. 9/29
- 16. JS Divergence for multiple shapes JS-divergence of shape densities JSπ (P1 , P2 , ..., Pn ) = H( π i Pi ) − πi H(Pi ) (1) where π = {π1 , π2 , ..., πn |πi > 0, πi = 1} are the weights of the probability densities Pi and H(Pi ) is the Shannon entropy. 10/29
- 17. Atlas estimation Formulation using JS-divergence N JSβ (P1 , P2 , ..., PN ) + λ ||Lf i ||2 i=1 N =H( β i Pi ) − βi H(Pi ) + λ ||Lf i ||2 . i=1 f i is the deformation function corresponding to point set X i ; Pi = p(f i (X i )) is the probability density for deformed point-set. 11/29
- 18. Multiple shapes: JS divergence JS divergence in a hypothesis testing framework: Construct a likelihood ratio between i.i.d. samples drawn from a mixture ( a πa Pa ) and i.i.d. samples drawn from a heterogeneous collection of densities (P1 , P2 , ..., PN ). The likelihood ratio is then M N k=1 a=1 πa Pa (xk ) Λ= N Na . a a=1 ka =1 Pa (xka ) Weak law of large numbers gives us the JS-divergence. 12/29
- 19. Group-wise Registration Results Experimental results on four 3D hippocampus point sets. 13/29
- 20. Shape matching via CDF I-divergences Model each point-set by a cumulative distribution function (CDF) Quantify the distance among cdfs via an information-theoretic measure [typically the cumulative residual entropy (CRE)] Minimize the dis-similarity measure over the space of coordinate transformation parameters 14/29
- 21. Havrda-Charvát CRE HC-CRE: Let X be a random vector in R d , we define the HC-CRE of X by ˆ EH (X ) = − (α − 1)−1 (P α (|X | > λ) − P(|X | > λ))d λ d R+ where X = {x1 , x2 , . . . , xd }, λ = {λ1 , λ2 , . . . , λd }, and |X | > λ means |xi | > λi , R+ = {xi ∈ R d ; xi ≥ 0; i ∈ {1, 2, . . . , d }}. d 15/29
- 22. CDF-HC Divergence CDF-HC Divergence : Given N cumulative probability distributions Pk , k ∈ {1, . . . , N}, the CDF-JS divergence of the set {Pk } is defined as HC (P1 , P2 , . . . , PN ) = EH ( πk Pk ) − πk EH (Pk ) k k where 0 ≤ πk ≤ 1, k πk = 1, and EH is the HC-CRE. 16/29
- 23. CDF-HC Divergence Let P = k πk Pk HC (P1 , P2 , . . . , PN ) ˆ ˆ −1 = −(α − 1) ( P α (X > λ)d λ− πk α Pk (Xk > λ)d λ) d R+ d R+ k ˆ ˆ 2 = πk Pk (Xk > λ)d λ − P 2 (X > λ)d λ (α = 2) d R+ d R+ k 17/29
- 24. Dirac Mixture Model Dk 1 Pk (Xk > λ) = H i (x, xi ) Dk i where H(x, xi ) is the Heaviside function (equal to 1 if all components of x are greater than xi ). 1 0.5 0 0 10 20 30 40 80 50 60 60 40 20 0 70 18/29
- 25. CDF-JS, PDF-JS & CDF-HC Before Registraion CDF−JS PDF−JS CDF−HC 3.5 3.5 3.5 3.5 3 3 3 3 2.5 2.5 2.5 2.5 2 2 2 2 1.5 1.5 1.5 1.5 1 1 1 1 0.5 0.5 0.5 0.5 0 0 0 0 0 1 2 0 1 2 0 1 2 0 1 2 Before Registraion CDF−JS PDF−JS CDF−HC 4 4 4 4 2 2 2 2 0 0 0 0 0 2 4 6 8 0 2 4 6 8 0 2 4 6 8 0 2 4 6 8 19/29
- 26. 2D Point-set Registration for CC Point Set 1 Point Set 2 Point Set 3 0.2 0.2 0.2 0.1 0.1 0.1 0 0 0 −0.1 −0.1 0 0.2 0.4 0.6 0 0.2 0.4 0.6 0 0.2 0.4 0.6 Point Set 4 Point Set 5 Point Set 6 0.2 0.2 0.2 0.1 0.1 0.1 0 0 0 −0.1 0 0.2 0.4 0.6 0 0.2 0.4 0.6 0 0.2 0.4 0.6 Point Set 7 Before Registration After Registration 0.2 0.2 0.2 0.1 0.1 0.1 0 0 0 −0.1 0 0.2 0.4 0.6 0 0.2 0.4 0.6 0 0.2 0.4 0.6 20/29
- 27. With outliers Before Registration After PDF−JS Registration After CDF−HC Registration 0.2 0.2 0.2 0.1 0.1 0.1 0 0 0 0.2 0.4 0.6 0.8 1 0.4 0.6 0.8 1 1.2 0 0.2 0.4 0.6 21/29
- 28. With different α values Initial Configuration α=2 0.2 0.2 0.1 0.1 0 0 0.5 1 0 0.2 0.4 0.6 α=1.1 α=1.3 α=1.5 α=1.7 0.2 0.2 0.2 0.2 0.1 0.1 0.1 0.1 0 0 0 0 0 0.2 0.4 0.6 0 0.2 0.4 0.6 0 0.2 0.4 0.6 0 0.2 0.4 0.6 α=1.9 α=3 α=4 α=5 0.2 0.2 0.2 0.2 0.1 0.1 0.1 0.1 0 0 0 0 0 0.2 0.4 0.6 0 0.2 0.4 0.6 0 0.2 0.4 0.6 0 0.2 0.4 0.6 22/29
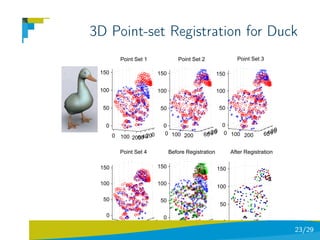
- 29. 3D Point-set Registration for Duck Point Set 1 Point Set 2 Point Set 3 150 150 150 100 100 100 50 50 50 0 0 0 0 0 100 200 40 0 0 100 200 40 0 60 20 0 100 200 40 60 20 60 20 Point Set 4 Before Registration After Registration 150 150 150 100 100 100 50 50 50 0 0 0 0 0 100 200 604020 0 100 200 40 0 60 20 0 0 100 200 50 23/29
- 30. 3D Registration of Hippocampi Point Set 1 Point Set 2 Point Set 3 100 0 100 0 100 0 100 100 100 200 200 200 0 0 0 50 50 50 10 10 10 20 20 20 0 0 0 Point Set 4 Point Sets Before Registration Point sets After Registration 100 0 100 0 100 0 100 100 100 200 50 50 50 0 200 200 0 0 10 5 10 20 0 10 0 0 15 20 24/29
- 31. Group-Wise Registration Assessment The Kolmogorov-Smirnov (KS) statistic was computed to measure the difference between the CDFs. With ground truth N 1 D(Fg , Fk ) N k=1 Without ground truth N 1 K= D(Fk , Fs ) N2 k,s=1 25/29
- 32. KS statistic for comparison Table: KS statistic KS-statistic CDF-JS PDF-JS CDF-HC Olympic Logo 0.1103 0.1018 0.0324 Fish with outliers 0.1314 0.1267 0.0722 Table: Average nearest neighbor distance ANN distance CDF-JS PDF-JS CDF-HC Olympic Logo 0.0367 0.0307 0.0019 Fish with outliers 0.0970 0.0610 0.0446 26/29
- 33. KS statistic for comparison (contd.) Table: Non-rigid group-wise registration assessment without ground truth using KS statistics Before Registration After Registration Corpus Callosum 0.3226 0.0635 Corpus Callosum with outlier 0.3180 0.0742 Olympic Logo 0.1559 0.0308 Fish 0.1102 0.0544 Hippocampus 0.2620 0.0770 Duck 0.2287 0.0160 27/29
- 34. KS statistic for comparison (contd.) Table: Non-rigid group-wise registration assessment without ground truth using average nearest neighbor distance Before Registration After Registration Corpus Callosum 0.0291 0.0029 Corpus Callosum with outlier 0.0288 0.0092 Olympic Logo 0.0825 0.0022 Fish 0.1461 0.0601 Hippocampus 13.7679 3.1779 Duck 15.4725 0.3280 28/29
- 35. Discussion I-divergences for shape matching avoid correspondence problem Symmetric, unbiased registration and atlas estimation Shape densities modeled as Gaussian mixtures, cumulatives directly estimated JS (pdf and cdf-based) and HC divergences used Estimated atlas useful in model-based segmentation 29/29